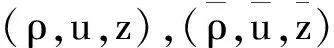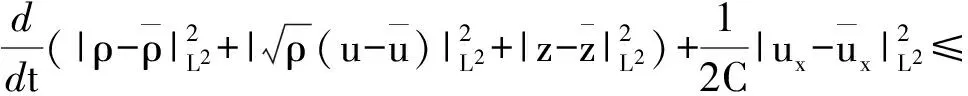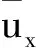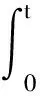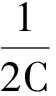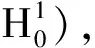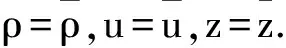一类燃烧非牛顿流强解的存在唯一性
2014-08-02谢嘉宁袁洪君
谢嘉宁,袁洪君
(1.东北财经大学数学与数量经济学院,辽宁 大连 116025;2.吉林大学数学学院,吉林 长春 130012)
一类燃烧非牛顿流强解的存在唯一性
谢嘉宁1,袁洪君2
(1.东北财经大学数学与数量经济学院,辽宁 大连 116025;2.吉林大学数学学院,吉林 长春 130012)
讨论了一类带有真空的燃烧非牛顿流的初边值问题,克服了非线性、奇异性以及真空出现等困难,得到了其局部强解的存在唯一性.
非牛顿流;燃烧;存在唯一性;真空
1 主要结果
本文着重探索燃烧非牛顿流体力学的数学理论.根据质量守恒定律,动量守恒定律和未反应流体的质量平衡规律,其数学模型
(1.1)
具有初边值条件
(1.2)
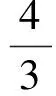
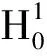
研究一般牛顿流体的文献已很多,对于可压缩燃烧牛顿流体的研究也取得了丰硕的成果.在无真空情形下,文献[1]研究一维不连续边值的模型得到了全局弱解.文献[2-3]也涉及了这个模型的测度解问题.文献[4]研究了一维自吸引粘性放射反应模型,得到了全局古典解的存在唯一性等.近来对于有真空的燃烧牛顿流体情形,Donatella Donatelli在文献[5]中,讨论了全局弱解的存在性.而对于研究燃烧非牛顿流体的文献还不是很多.
在本文中,我们通过更精细的估计,克服了方程组由双曲和抛物两类方程组成的强耦合性、由动量守恒方程带来的奇异性和非线性以及真空带来的困难,给出了局部强解的存在唯一性.我们的主要结果如下:
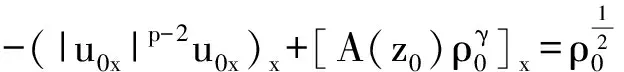
(1.3)
在I上几乎处处成立.则存在一个时间T*∈(0,∞),问题(1.1)—(1.2)在ΩT*上存在唯一的解(ρ,u,z),并具有下列性质:
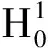
(1.4)
由于证明需要,我们给出如下引理:
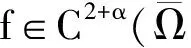
其中d(Ω)表示Ω的长度.
2 近似解的构造及一致估计
为了得到定理1.1,我们考虑关于初值的正则化问题:
(2.1)
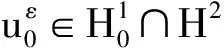
我们直接构造(1.1)—(1.2)的近似解,具体过程如下:
先定义u0=0,z0=0,代入下列方程中,我们可以得到一串光滑函数列(ρk,uk,zk),它们是下列初边值问题的解:
(2.2)
(2.3)
(2.4)
(2.5)
其中
πk≡A(zk)(ρk)γ,A(s)>0,s∈R,γ>1,
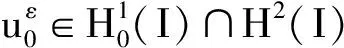
(2.6)
的光滑解.
对于已知的光滑函数uk-1,方程(2.2)分别存在唯一的解ρk,且由特征线法和Sobolev不等式得出
(2.7)
对所有的t∈(0,T).
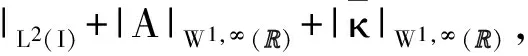
为了方便证明我们建立辅助函数
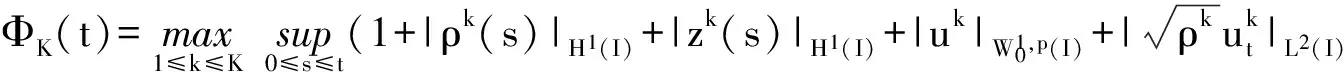
引理2.1
(2.8)
(2.9)
(2.10)
对所有的k(1≤k≤K),其中正常数C仅依赖于M0.
引理的证明可参照文献[6].
引理2.2
(2.11)
(2.12)
对所有的k(1≤k≤K),其中正常数C仅依赖于M0.
证明 对(2.2)式两边同乘以ρk,并在(0,1)上积分,我们可以得到
(2.13)
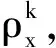
(2.14)
由(2.13)和(2.14)式可以得到
(2.15)
对(2.4)式,同理由Gronwall不等式可以得到证明结果.
综合引理1.1和1.2,有
(2.16)
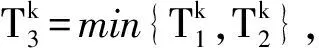
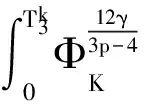
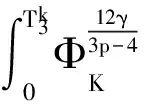
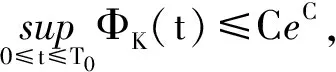
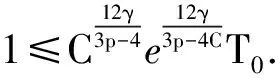
其中C是正常数,仅依赖于γ,M0.
因此,由上述推导,对所有的1≤k≤K,下列一致估计成立:
(2.17)
C*是正常数仅依赖于γ,M0.
由近似方程(2.2),(2.4)得到:
(2.18)
(2.19)
综合上述情况,我们可以得到:
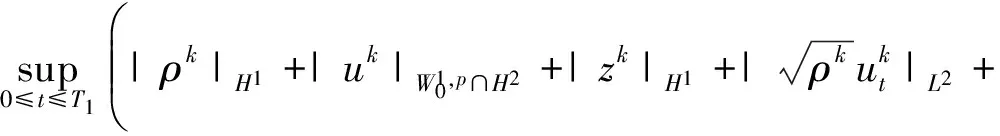
(2.20)
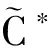
3 近似解的收敛性
有了一致估计(2.17)和(2.20),就可以证明近似解序列(ρk,uk,zk)的极限存在.为此,我们定义:
(3.1)
由(2.2),(2.3),(2.4)式,参照文献[6]可得:
(3.2)
(3.3)
(3.4)
其中:
综上所述,关于t在(0,t)∈(0,T1)上积分,利用Gronwall不等式可以得到
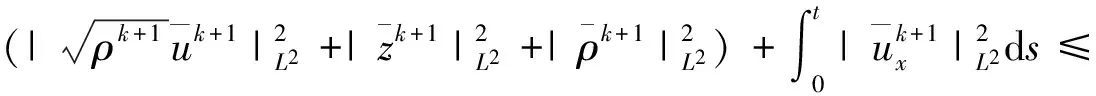
因而,我们选定η,然后再选不定期足够小的T*,使得4C(T*+δ)<1,T* (3.5) 其中C为一常数,仅依赖于M0. 由(2.7)式,可有ρk(x,t)>0,对所有的t∈(0,T*).因此,由(3.5)式可得下列收敛性: 当k→∞时, (3.6) ρk→ρε于L∞(0,T*;L2(I))强收敛, (3.7) zk→zε于L∞(0,T*;L2(I))强收敛. (3.8) 由于逼近问题的初值(ρ0,u0,z0)不依赖于k,则(ρ0,u0,z0)仍然处处满足边值问题(2.6).且由范数的下半连续性可得,(ρε,uε,zε)也满足下列一致估计: (3.9) 有了(3.6),(3.7),(3.8)三类收敛性,我们很容易验证(ρε,uε,zε)为方程 (4.1) 具有初边值条件 的解(方法参考文献[6]). 为了得到初边值问题解的存在性,我们还需要证明解(ρε,uε,zε)满足性质(1.4). (4.2) 其次,证明 对于上式右端第二项,可写为 因此 现在要想得到本节的主要结论,还需要关于ε取极限. 由于在我们所得的一致估计中的控制常数均不依赖于ε,则由一致估计(3.9)可得,存在{(ρε,uε,θε)}的一个子列{(ρεj,uεj,zεj)},不妨仍记为{(ρε,uε,zε)},当ε→0时,有下列收敛性: ρε→ρ于L∞(0,T*;L2(I))强收敛, (4.3) (4.4) zε→z于L∞(0,T*;L2(I))强收敛. (4.5) 且(ρ,u,z)也满足一致估计: (4.6) 引理3.1的详细证明参见文献[6]. (4.7) 的唯一解,并几乎处处满足方程(4.7). 因此有了(4.3),(4.4),(4.5)三种收敛性,且(ρ,u,z)满足一致估计,那么我们就可以用与之前相同的方法,证明(ρ,u,z)问题的解,并且满足性质1.4.因而,无真空时解的存在性得证. (5.1) 根据相容性条件和经典的椭圆抛物方程理论,我们可以得到如下收敛性:存在δ的子列{δj}(不妨记为它本身).当δ→0时有 并且u0满足定理1.2的相容性条件.则对任意的δ>0,由之前的证明可知 因此,与之前的证明类似,我们可以证明问题(1.1)—(1.2)解的存在性,而关于(ρ,u,z)连续性的证明与无真空情形证明是一样的,在此不再赘述.于是定理1.1存在性得证. (6.1) (6.2) (6.3) 综合上式,最后我们有 (6.4) 其中: 由Gronwall不等式可得 因而,定理1.1的唯一性证毕.于是定理1.1得证. [1] GUI-QIANG CHEN,DAVID HOFF,KONSTANTINA TRIVISA.Global solutions to a model for exothermically reacting compressible flows with large discontinuous initial data[J].Arch Rational Mech Anal,2003,166:321-358. [2] BUCK J D.The mathematics of combustion[M].Frontriers in Applied Mathematics,2 Society of Industrial and Applied Mathematics,Philadelphia PA:SIAM,1985:22-201. [3] WILLIAMS F A.Combustion theory[M].New Jersey:Addison-Wesley,1965:19-136. [4] UMEHARA M,ATUSI TANI.Global solution to the one-dimensional equations for a self-gravitating ivscous radiative and reactive gas[J].J Differential Equations,2007,234:439-463. [5] DONATELLA DONATELLI,KONSTNTINA TRIVISA.A multidimensional model for the combustion of compressible fluids[J].Arch Rational Mech Anal,2007,185:397-408. [6] XU X,YUAN H.Existence and uniqueness of solutions for a class of non-Newtonian fluids with singularity and vacuum[J].J Differential Equations,2008,245:2871-2916. [7] GALDI G P.An introduction to the mathematical theory of the Navier-Stokes equations[M].New York:Springer-Verlag,1994:25-134. [8] LADYZHENSKAYA O A.The Boundary value problems of mathematical physics[M].New York:Spring-Verlang,1985:36-122. (责任编辑:陶 理) Existence and unique of the strong solution for a class of combustion non-Newtonian fluids XIE Jia-ning1,YUAN Hong-jun2 (1.School of Mathematics and Quantitative Economics,Dongbei University of Finance and Economics,Dalian 116025,China;2.Institute of Mathematics,Jilin University,Changchun 130012,China) This paper deals with a class of reactive gas flow for non-Newtonian fluids in one-dimensional initial value and obtain the local existence and uniqueness of solutions by overcoming the difficulties of nonlinear,singularity,vacuum and so on. non-Newtonian;reactive gas flow;existence;vacuum 1000-1832(2014)04-0015-07 10.11672/dbsdzk2014-04-003 2014-05-24 国家自然科学基金资助项目(11226326,11301060,71201019);东北财经大学青年科研人才培育项目(DUFE2014Q66). 谢嘉宁(1984—),女,博士研究生,主要从事非线性偏微分方程研究;通讯作者:袁洪君(1966—),男,教授,博士研究生导师,主要从事非线性偏微分方程研究. O 175.2 [学科代码] 110·47 A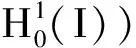
4 无真空解的存在性
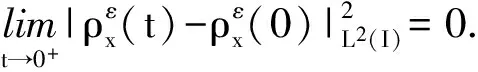
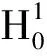
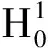
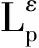
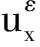
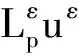
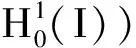
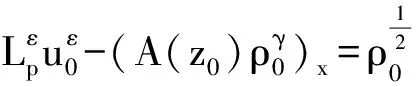
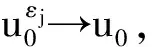
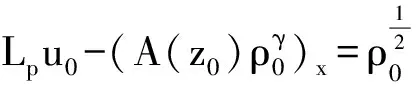
5 真空情形解的存在性
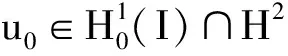
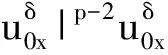
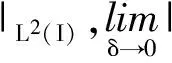
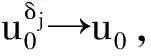
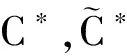
6 解的唯一性