基于pair copula-SV模型的资产组合风险度量

刘昆仑

(齐鲁师范学院 数学学院，山东 济南 250200)

波动是金融市场最重要的特征之一，常用的波动模型有广义自回归条件异方差模型(generalized autoregressive conditional heteroscedasticity，GARCH)和随机波动模型(stochastic volatility，SV)，其中SV模型在长期波动性的预测能力和波动率序列的稳定性上都优于GARCH模型，能更好地捕捉到金融序列的尖峰厚尾性[1].由于一般金融资产间的相关关系并非是线性的，因此不能简单地用相关系数进行度量.1959年Sklar[2]提出了copula函数，此函数可以用来描述变量间的非线性相关关系，与传统的n维copula函数相比，它能更加灵活和准确地描述出资产间的尾部相关结构.随着经济全球化与金融一体化的发展，金融风险日趋复杂多样，在金融风险管理中copula-SV模型被广泛使用[3-4].本文构造了一个pair copula-SV模型，并用此模型计算了资产组合的风险价值(Value at Risk，VaR).在实证分析中，选取4支股票构成资产组合，计算其VaR，并进行了Kupiec检验，其检验结果表明，此模型能很好地度量金融资产组合的风险价值.

1 pair copula分解模型

根据Sklar定理，联合分布函数可以通过边缘分布函数Fi(xi),i=1,2,…,n和copula函数表示成F(x1,x2,…,xn)=C1,2,…,n(F1(x1),F2(x2),…,Fn(xn))，则联合概率密度函数为

f(x1,x2,…,xn)=c1,2,…,n(F1(x1),F2(x2),…,Fn(xn))·f1(x1)…fn(xn)，

(1)

其中c1,2,…,n(·)为n维copula函数，fi(xi)为边缘概率密度函数.

随机向量X=(X1,X2,…,Xn)的联合概率密度函数可以分解为

f(x1,x2,…,xn)=fn(xn)fn-1|n(xn-1|xn)fn-2|n-1,n(xn-2|xn-1,xn)…f1|2,…,n(x1|x2,…,xn).

(2)

当n=2时，由(1)式得f(x1,x2)=c12(F1(x1),F2(x2))·f1(x1)·f2(x2).又因为f(x1,x2)=f2(x2)f(x1|x2)，故

f(x1|x2)=c12(F1(x1),F2(x2))·f1(x1).

(3)

当n=3时，同理有

f(x1|x2,x3)=c13|2(F(x1|x2),F(x3|x2))·f(x1|x2)，

(4)

其中c13|2(·,·)是转换变量F(x1|x2)和F(x3|x2)的pair copula函数.当n=3时，条件概率密度f(x1|x2,x3)还可以分解为f(x1|x2,x3)=c12|3(F(x1|x3),F(x2|x3))·f(x1|x3).将(3)式代入(4)式，得f(x1|x2,x3)=c13|2(F(x1|x2),F(x3|x2))·c12(F1(x1),F2(x2))·f1(x1).以此类推，条件密度函数[5]可以分解为f(x|v)=cxvj|v-j(F(x|v-j),F(vj|v-j))·f(x|v-j)，其中vj是n维向量v的一个分量，v-j是向量v中除去vj后的n-1维分量.cxvj|v-j(·,·)称为pair copula密度函数，它包含了两个条件分布函数F(x|v)，其求解公式[6]为

(5)

由以上推导可知，(2)式中的每一个条件密度函数都可以分解为一系列pair copula密度函数与边缘密度函数的乘积.

近年来，pair copula方法经研究者们的不断完善[5-7]，已作为构建多变量联合分布的新方法而得到广泛应用，与多维copula函数相比，pair copula方法能更好地描述高维变量间的相关结构.一个n维分布函数可以有多种pair copula分解方法，Bedford等[7]介绍了一种利用正则藤(the regular vine)图形来描绘联合密度函数分解形式的方法，常用的正则藤有Canonical藤和D藤，每个藤结构图由树、边和节点组成，两种不同藤的图形结构适用于资产间不同相关关系的序列集合.Canonical藤联合密度函数的分解公式为

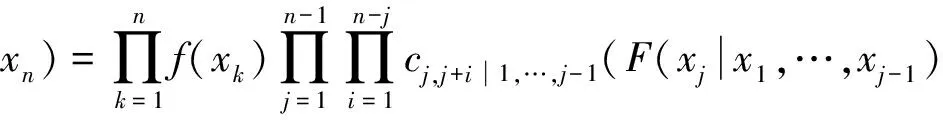
(6)

D藤联合密度函数的分解公式为

(7)

pair copula模型参数一般采用极大似然估计法进行估计，Canonical藤的对数似然函数为

(8)

D藤的对数似然函数为

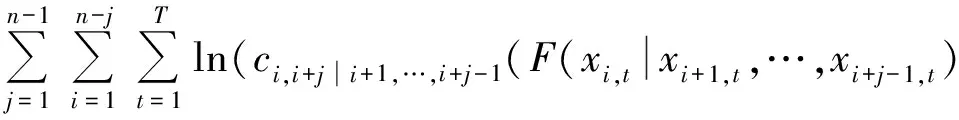
(9)

其中i表示每棵树中节点的个数，j表示树的个数，Θ表示pair copula密度函数的参数集.

2 pair copula-SV模型下资产组合VaR的计算

2.1 SV模型、参数估计及检验

SV模型是假设波动率服从某种潜在的不可观测的随机过程，此模型能极大程度地拟合金融波动.目前SV模型可分为：标准的SV模型(SV-N)、厚尾的SV模型(SV-T或SV-GED)、考虑预期收益的SV模型(SV-M)、长期记忆的SV模型(LM-SV)、考虑杠杆效应的SV模型(Leverage SV)和Box-Vox-SV模型(一类非线性模型)等.因金融序列波动的异方差性和尖峰厚尾性，本文选用SV-T模型，其具体形式如下：

(10)

ht=μ+φ(ht-1-μ)+ηt.

(11)

其中：yt为第t日的收益率；εt为独立同分布的白噪声过程，εt服从自由度为ω、均值为0的t分布,当ω<4时，t分布的峰值不存在,当4<ω<∞时，峰值大于3,当ω→∞时，εt具有渐进正态分布；φ为持续性参数，当|φ|<1时，SV模型是协方差平稳的；ht为潜在波动，服从参数为φ的高斯AR(1)过程；ηt为独立同分布的波动的扰动水平，服从均值为0、方差为τ2的正态分布[8].

由于SV模型中包含不可观测的潜在变量，涉及的无条件矩和似然函数要通过高维积分进行计算，因此很难用极大似然估计法进行参数估计.目前常用的参数估计方法有：矩类估计法(GMM)、伪极大似然法(QML)、模拟极大似然法(SML)、马尔可夫蒙特卡洛法(MCMC)和蒙特卡洛极大似然法(MCML)等.本文选用MCMC法，此方法的基本思想是通过建立一个平稳分布为π(θ)的马尔可夫链来得到π(θ)的样本，然后基于这些样本做出各种统计推断，并且MCMC模拟可以通过WinBUGS软件实现.

2.2 pair copula-SV模型及参数估计

为了估计资产组合的风险价值，本文选用SV模型拟合金融资产的边缘分布，用pair copula函数来描绘组合中资产间的相关结构，这样就构造了pair copula-SV模型，然后再使用Monte Carlo模拟法估计组合的VaR值.藤结构中每个pair copula函数都是一个二元copula函数，可以根据两两资产间不同的相关关系，选择不同的二元copula函数，常用的copula函数有正态copula函数、t-copula函数、阿基米德copula函数族等.在n维copula模型中，资产组合的相关关系可以用一个固定的copula函数描述，而pair copula模型中的任意两个资产之间可以自由选择适合的copula函数，所以pair copula模型比传统的n维copula模型具有很大的优越性.

SV模型中的参数估计可通过基于Gibbs的MCMC方法实现，而pair copula模型的参数估计可以分为两步：首先，根据已估计出的边缘分布的结果，用极大似然估计的方法对藤结构图中每棵树上的二元copula函数进行参数估计，得到参数初值[10]；其次，根据(8)或(9)式进行极大似然估计，得到pair copula模型中参数的终值.

2.3 VaR的计算及检验

VaR是指在一定时期内，一定的置信水平1-α下，金融市场交易损失值的临界点，其中α表示超过临界点的可能性.因VaR具有概念简单、便于计算的优点，因此被应用于股票、债券、期货、期权等多种资产形式.VaR计算的关键是准确描述资产组合的概率分布，即只要有了资产的分布情况，就可以估计出资产的风险价值.

假设组合的收益率为rt=ω1r1,t+ω2r2,t+…+ωnrn,t，其中ri,t为第i个资产在t时刻的收益率，ωi为第i个资产在组合中占得的权重，则在显著性水平α下的VaR应满足如下关系式：

P(rt≤VaRt(α)|Ωt-1)=α.

(12)

本文通过Monte Carlo方法计算组合的VaR，再对其准确性进行检验，检验法中最具代表性的方法是Kupiec的失败率检验法.这里所构造的统计量为

LR=-2 ln[(P0)N(1-P0)T-N]+2 ln[(N/T)N(1-N/T)T-N],

其中：P0=α，1-P0为置信水平；T为实际考察天数；N为失败天数，即实际损失超过VaR的天数.

3 实证分析

3.1 数据的选取和描述性统计

选取“市北高新(600604)”、“迪康药业(600466)”、“华域汽车(600741)”、“亚盛集团(600108)”4支股票构建投资组合，时间为2008年7月1日—2013年12月31日.首先，将日期不相同的数据剔除，共得到1 091组数据；其次，求出4支股票收盘价的收益率ri,t，ri,t=100×ln(pi,t/pi,t-1)，其中pi,t是第i支股票在t时刻的收盘价，i=1,2,3,4.

首先对股票收益率数据进行统计分析，结果见表1.从表1中可以看出，4支股票的峰度值均大于3，偏度值不等于0，即数据具有“尖峰厚尾”性.J-B统计量的值均大于临界值，且P值为0，说明收益率数据在5%的显著性水平下拒绝正态分布的假设.运用SV模型的前提是序列必须平稳，本文选用单位根检验法(ADF)对收益率序列的平稳性进行了检验.从表1的结果可以看出，ADF值都小于1%显著性水平下的临界值(-3.44)，且P值接近于0，故收益率序列是平稳的，可以使用随机波动模型.通常ADF检验可以通过Eviews 5.0软件来实现.

表1 股指收益率的描述性统计分析

3.2 SV模型的参数估计

使用厚尾的SV-T模型分别对各支股票的收益率数据进行拟合，然后再使用MCMC方法，通过WinBUGS软件进行参数估计和检验，结果见表2.以表2中“市北高新”的数据为例，对参数估计结果进行分析.分析结果显示：波动水平μ的贝叶斯估计值为-6.453 7，置信水平为95%的后验置信区间为[-7.363 1，-5.436 8]；波动持续性参数φ的估计值为0.968 6，置信水平为95%的后验置信区间为[0.957 5，0.985 2]，其值接近于1表明股指数据的波动性冲击是连续的；参数τ的值为0.231 6，代表波动性的扰动水平；自由度ω的值为17.364 3，4<ω<∞时，说明εt的峰值大于3，故拒绝收益率序列服从正态分布的假设.

其余3支股票参数的分析结果类似于“市北高新”的结果(其分析过程省略).4支股票的DIC值接近，说明拟合效果相当，这表明可以使用SV-T模型进行数据处理.K-S检验的P值都大于0.05，说明在5%的显著性水平下，各股票数据经积分变换后的收益率序列都服从[0,1]上的均匀分布，符合copula函数的要求.K-S检验可借助SPSS软件来完成.

表2 SV模型的参数估计及检验

3.3 pair copula函数的参数估计

沿用2.2中的思路，利用Matlab软件对pair copula函数的参数进行了估计.为表述上的方便，分别用数字1、2、3、4代表4支股票.因股票数据的“尖峰厚尾”性，本文选择t-copula函数作为每棵树上pair copula函数的类型；为了选择合适的藤分解结构，首先分别算出Canonical藤和D藤下的参数，然后使用AIC准则[11]进行检验,其计算公式为：AIC=-2×极大似然值+2×模型参数个数，AIC的值越小，模型的拟合效果越好，此过程可通过SPSS软件来实现.对于4维藤分解结构，由(6)和(7)式可知有6个pair copula函数，每个pair copula函数是一个2维t-copula，包含2个参数(线性相关系数ρ和自由度ν)，共12个参数.参数估计和检验结果见表3.

表3 Pair copula的参数估计及检验

由表3可知，D藤的AIC值小于Canonical藤的AIC值，说明D藤的拟合优度高于Canonical藤，故本文选择D藤.在D藤分解结构中，对应的每棵树上的变量之间是相互独立的，这也与一般情况下股票数据相互独立的惯例相吻合.

3.4 投资组合VaR的计算

估计出SV模型和pair copula模型的参数后，就可以使用Monte Carlo方法计算VaR.对于构造的4维联合分布，VaR的计算步骤[12]为：

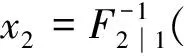
步骤4 重复以上步骤1 000次，求出VaR的平均值即为t时刻(即第t日)的估计值.

利用以上算法计算出的VaR结果及Kupiec检验结果见表4.由表4数据可知，95%和99%的置信水平下的VaR分别为0.585 3和0.746 9，对应的LR值都小于临界值，这说明本文模型估计出的VaR能较好地度量资产组合的金融风险.

表4 资产组合的VaR及Kupiec检验

4 结论

本文将pair copula方法和SV模型相结合，构造了pair copula-SV模型，以此来度量金融资产的VaR值．本文结果表明，此模型能更好地捕捉金融资产的尖峰厚尾性及资产间的尾部相关性.本文模型的参数较多，计算量也比较大，但随着一些新的参数估计方法的研究，以及更有效的专用软件包的使用，本文模型将会得到更好的应用.

参考文献：

[1] 余素红,张世英.SV与GARCH模型对金融时间序列刻画能力的比较研究[J].系统工程,2002,20(5):28-33.

[2] Sklar A. Fonctions de repartition an dimensions etleurs marges[J]. Publication de 1’Institut de Statistique de 1’Universite de Paris, 1959,8:229-231.

[3] 战雪丽,张世英.基于Copula-SV模型的金融投资组合风险分析[J].系统管理学报,2007,16(3):302-306.

[4] 包卫军,徐成贤.基于SV-Copula模型的相关性分析[J].统计研究,2008,25(10):100-104.

[5] Aas K, Czado C, Frigessi A. Pair-copula constructions of multiple dependence[J]. Insurance:Mathematics and Economics, 2009,44:182-198.

[6] Joe H. Multivariate models and dependence concepts[M]. London:Chapman & Hall, 1997.

[7] Bedford T, Cooke R M. Vine-a new graphical model for dependent random variables[J]. Annals of Statistics, 2002,30(4):1031-1068.

[8] 郭卫超.基于SV模型的中国股市波动性实证研究[D].青岛:青岛大学经济学院,2010:17.

[9] 刘凤芹.基于DIC准则的SV族模型的比较[J].统计与决策,2004,9(177):24-25.

[10] 黄恩喜,程希骏.基于pair copula-GARCH模型的多资产组合VaR分析[J].中国科学院研究生院学报，2010,27(4)：440-447.

[11] Akaike H. Fitting autoregressive models for prediction[J]. Ann Inst Statics Math, 1969,21:不详.

[12] 高江.藤Copula模型与多资产投资组合VaR预测[J].数理统计管理,2013,32(2):247-258.