基于TSP的孔群加工路径优化算法
2014-08-02颜国霖
颜国霖
(黎明职业大学 机电及自动化学院, 福建 泉州 362000)
在模具顶针板和面针板加工中孔群加工占有很大比重,但由于孔的位置不同、孔径大小不一,在孔加工时换刀时间和空走刀时间占总加工时间的30%左右[1],大大降低了生产效率;因此,寻求一种孔群加工最短路径的优化算法对提高孔群加工效率具有重要意义.目前,提高孔群加工效率普遍采用贪心算法、蚁群算法或蚁群算法与其他算法相结合的方法[2-5],这些算法虽然在一定程度上优化了加工路径,但采用贪心算法产生的是全局最优解[6],使刀具空走刀行程增加,实际求得的解并非最优,而采用蚁群算法进行优化会造成计算量和搜索时间增加,易出现停滞现象.针对孔群中不同孔径加工问题,本文构造了蚁群算法与2-OPT算法相融合的优化算法,并与贪心算法、基本蚁群算法进行了比较,最后在模具顶针板孔群加工实验中验证了本文算法的有效性.
1 路径优化算法的数学模型
使用数控钻孔机进行孔加工时,为了将换刀次数降到最少,通常会使用同一把刀从下刀点开始,沿着最短路径加工完所有可能加工的孔,然后再换另一把刀加工另一尺寸的孔,如此循环.此过程可视为典型的旅行商问题(travelling salesman problem,TSP)[7],即刀具充当旅行商角色,孔位置代表城市位置,孔群路径优化目标则是刀具路径最小值.该问题用图论可描述为:给定一个带权有向图G=(V,E),V表示G的顶点集,V={1,2,…,n},E表示图G的边集,dij表示任意两孔之间的距离,也就是vi指向vj的边的权重,i,j=1,2,…,n.图G的最短路径问题就是求解从下刀点到V中其他各顶点的最短路径长度,其中:路径长度定义为路径上各条边的权重之和;约束条件为刀具从换刀点开始,无重复地加工每一个孔,且遍历所有的孔.其数学模型为
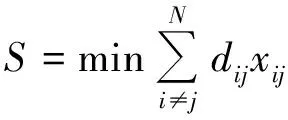
(1)
其中n表示零件上的孔数.当刀具在规划加工路线上时,xij=1;否则,xij=0.
2 智能融合算法
假设有m只蚂蚁,di表示任意两孔之间的距离,τij(t)表示t时刻残留在第i个孔和第j个孔连线上的信息量.初始时刻t=0,各条路径上有少量的信息τij(0),根据各条路径上信息量的多少,t时刻位于某一个孔的蚂蚁k(k=1,2,…,m)一次只能选择一个目标孔.根据伪随机比例规则,当蚂蚁k从孔i移动到孔j时满足如下关系式:
(2)
(3)
其中N(S)是可行元素的集合,系数α和β控制着信息τij和启发式信息ηij的相对重要性.在孔群加工中,ηij表示孔i和孔j间的期望程度,设为距离的倒数.在每一次迭代中,所有的m只蚂蚁都更新它自己所找到的解的路径上的信息素.信息素τij的更新规则如下:
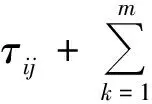
(4)
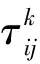

(5)
其中Q是一个常数,Lk是蚂蚁构建的路径长度.
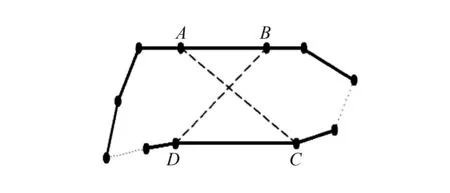
图1 2-OPT算法原理图
在蚁群算法最后阶段引入2-OPT算法,即从一条初始可行解开始,通过交换路径中的2条互不相邻的边,做一次2-OPT交换,如图1所示.该方法可使算法不易陷入局部最优解,能够增大解突变的机率,扩大蚂蚁搜索空间,加快搜索速度.两种算法的融合实现步骤如下:
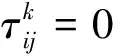
2) 将m只蚂蚁放到节点n上,每一只蚂蚁都从出发点A1开始,T表示蚂蚁选择孔的集合,循环次数N←N+1, 蚂蚁数量k←k+1.
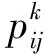
4) 2-OPT优化.从蚁群搜索中获取初始路径T,设被替代边集为X, 替代边集为Y,X和Y为空集;i=1,不断地增加i后,实施一个局部变换即用新边替代旧边,使得xi,yi进入X集和Y集,以此不断减少路径长度,直到获得较短路径为止,然后转入i=2,….
5) 全局更新.当蚂蚁成功地完成一次迭代最佳路线后,根据公式(4)和(5)全局更新当前最佳路径上的信息素τij.
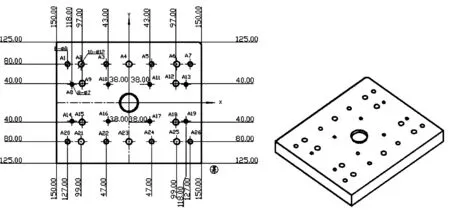
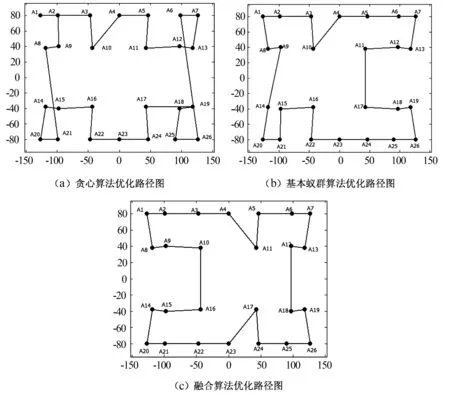
6) 算法结束.若蚂蚁数k 以图2所示为例,该板需要加工的孔有3类,直径分别为7、8、12 mm,加工孔数分别对应的是8、8、10个.选取顶针板上顶面中心为编程坐标系原心.根据数控加工工序的不同,所用的钻头直径大小不同,但其中有重叠.为了预制孔的精确定位,引导麻花钻进行孔加工,以减少加工误差,首先用中心钻点孔,然后根据不同孔径大小,选用不同直径麻花钻钻孔,最后根据加工精度要求进行铰孔.具体加工工序为钻中心孔φ3→钻孔φ6.8→钻孔φ7.8→钻孔φ11.8→铰孔φ7→铰孔φ8→铰孔φ12. 图2 模具顶针板零件图 为了验证优化算法的效果,选用贪心算法、蚁群算法与融合算法分别进行4种刀具走刀路径优化比较.参数设置如下:蚂蚁数量m=20,信息素重要性系数α=1,启发值重要性系数β=5,信息素挥发系数ρ=0.1,信息素增加强度系数Q=100.以φ3中心钻走刀路径为例,不同算法的优化结果如图3所示,最优解迭代搜索过程如图4所示.由图3和图4可知:贪心算法最短路径为1 198.92 mm;蚁群算法优化所得路径长度平均值为1 466.46 mm,最短路径为1 147.55 mm;融合算法优化所得路径长度平均值为1 441.17 mm,最短路径为1 138.96 mm. 图3 不同算法下φ 3中心钻路径实验结果图 (a)基本蚁群算法 (b)融合算法 对比表1中3种算法对4种刀具路径优化后的路径长度可知,融合算法优化刀具路径比贪心算法分别缩短了5.27%、1.72%、1.36%、3.81%,比蚁群算法分别缩短了0.76%、1.52%、1.05%、3.46%,由此可知,融合算法比贪心算法、蚁群算法更能有效地节省走刀时间,提高加工效率.在模具加工中,孔的数量越多,效果越明显. 表1 不同算法、不同刀具所优化的路径长度 本文针对基本蚁群算法、贪心算法的不足,提出将蚁群算法与2-OPT算法相结合的融合算法.路径优化实验结果表明,本文提出的算法在模具顶针板加工路径规划上,可有效地缩短走刀路径,降低顶针板数控加工时间,节约加工成本. 参考文献: [1] 周鲲,邵华.基于Hopfield算法的孔群加工路径规划 [J].模具技术,2003,21(1):48-50. [2] 潘海鸿,刘晓琳,廖小平,等.钣金激光切割加工CAD/CAM软件的孔群加工路径算法 [J].组合机床与自动化加工技术,2013(11):110-118. [3] 陈琳,刘晓琳,潘海鸿,等.孔群分类加工的优化算法 [J].制造业自动化,2013,39(9):45-49. [4] 曲晶,肖世德,熊鹰.基于蚁群算法的PCB孔加工路径优化 [J].机电工程,2007,40(10):48-51. [5] Dorigo M, Birattari M, Stutzle T. Ant colony optimization:artificial ants as a computational intelligence technique [J]. IEEE Computational Intelligence Magazine, 2006,1(4):28-39. [6] 张军,钟竞辉.算法分析与设计 [M].北京:清华大学出版社,2011:177-185. [7] 孙业荣,姚斌,张春雨.基于TSP和塑料模具顶针板孔群加工路径优化问题的研究 [J].机械设计与制造,2010,10:241-243.3 路径优化实验结果与分析
3.1 路径优化实验
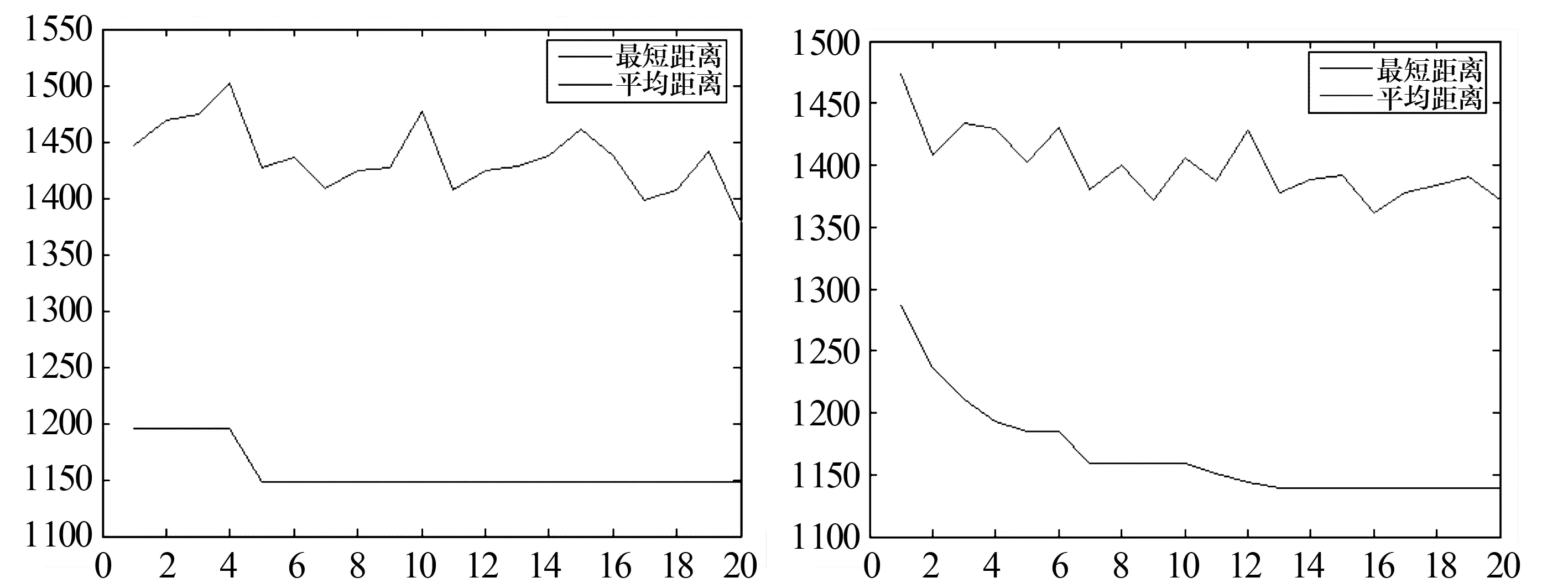
3.2 实验数据分析
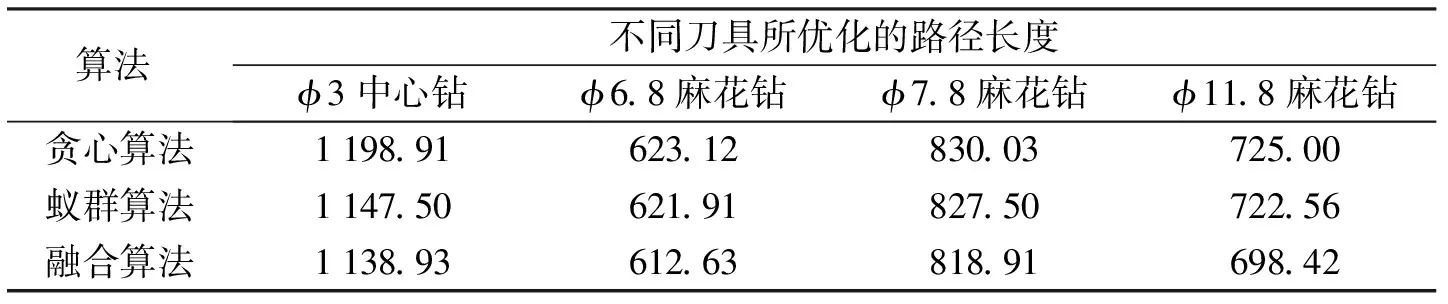
4 结束语
