一种基于RPC模型的SAR影像几何精纠正新方法

刘美琳

(1.兰州交通大学，兰州 730070；2.中国测绘科学研究院，北京 100830)

1 引 言

通常情况下，通过雷达获取的影像，并不能够直接为人们所用，这是因为SAR传感器是侧视成像，具有透视收缩、叠掩和雷达阴影等几何特征，这些由于地形起伏引起的几何形变给用户理解SAR影像并从中提取专题信息造成了困难；此外，SAR影像通常是按照方位向和距离向存储，必须转换到地理坐标系下，才能和其他空间数据开展联合分析和信息提取[1]。几何纠正的核心问题是确定描述地面点坐标与影像行列坐标之间的对应关系[2]，生成一幅消除几何畸变的地理坐标系存储的影像。SAR影像的几何纠正在影像融合、影像分类和灾害监测等应用中必不可少；并且随着新一代高分辨率、全极化SAR数据的广泛应用，针对新型数据研究新的几何精纠正算法具有重要的意义。

RPC模型是近几年发展起来的新型SAR影像定位模型。Tao于2001年根据RPC的有理函数系数的求解方式将有理函数模型分为“依赖于地形”和“独立于地形”两种方案[3]。Di等在2003年比较了有理函数模型和严格传感器模型的纠正结果，同时讨论了从PRC恢复严格传感器模型的可行性[4]。Fraser等在2006年系统研究了如何从严格成像模型计算RPC模型，介绍了外方位元素偏差补偿的求解方法，同时总结了误差传播规律[2]。秦绪文等2006年首次将RPC模型应用于ERS SAR卫星影像的定位处理中，对比了RPC模型参数在9种形式下的求解精度，并对控制格网点大小及高程分层的影响作出了评价[5]。张过等2008年将RPC模型引入到对TerraSAR-X和COSMO SkyMed卫星高分辨率SAR影像的几何纠正的处理中，结合距离多普勒模型，拟合出RPC的有理函数系数，并获取了正射影像[6]。

采用RPC模型作为SAR传感器模型具有运算效率快、简单、保密性好等特点。然而，目前RPC模型在SAR影像模型定位计算中还未得到广泛的运用。有关RPC模型的研究没有系统地总结基于RPC模型在SAR影像几何精纠正处理中流程，缺乏RPC模型精化对几何精纠正的精度影响评估。本文采用TerraSAR-X和Radarsat-2的SAR影像数据进行实验，将RPC模型应用于SAR影像几何精纠正过程，利用控制点对RPC模型进行模型精化，并系统地对几何精纠正的精度进行了评价。

本文首先介绍了RPC模型算法原理和几何精纠正的算法流程，并对精度评定的方法进行了总结；接着利用根河地区TerraSAR-X和Radarsat-2的SAR影像和辅助DEM进行实验验证，并对RPC模型的定位精度和几何精纠正获取的正射影像的绝对精度做出评价；最后对本文进行了总结。

2 RPC定位模型

2.1 RPC模型算法

RPC模型多项式如式(1)、式(2)所示：

(1)

(2)

其中，(r，c)表示SAR影像的方位向和距离向图像坐标，(P，L，H)表示对应的地理坐标经度、纬度和高度。为了防止算法运算时矩阵病态，(r，c，P，L，H)进行了归一化处理。Nr，Nc，Dr和Dc为多项式函数，最高阶数为3。RPC模型进行定位计算步骤如下所示[6]：

(1)建立虚拟控制点和检查点格网。首先，根据影像覆盖区的高程分布范围，建立具有不同的高程的控制点分布层，每层均匀分布虚拟控制格网点。然后根据R-D物理模型计算每个虚拟控制点对应的图像坐标，得到包含控制点地理坐标(P，L，H)及其对应图像坐标(r，c)的点对。由于RPC模型按照式(1)、式(2)中分母的异同、分母是否为1以及多项式阶数，可以分为9种情况[6]。本文采用了式(1)、式(2)分母不同，且不为1，多项式阶数为3阶的方案，共有78个RPC模型参数；因此至少需要39个虚拟控制点才能求解出78个RPC参数。获取足够多的控制点后，可以建立起RPC模型参数的法方程，求解得到RPC模型参数。

(2)RPC模型求解。假设上一步已经建立了具有n个控制点的格网，W为权矩阵，A为系数矩阵，X为未知数矩阵，L为常数项矩阵，则对n组观测量(ri，ci，Pi，Li，Hi)(i=1，2，…，n)可建立的法方程如下：

Δ=WAX-WL

(3)

其中，W为权矩阵，A为系数矩阵，X为未知数矩阵，L为常数项矩阵。通过最小二乘法进行迭代，求解出RPC函数中未知数矩阵X，即RPC模型参数。

(3)RPC模型定位精度评定。对于SAR影像而言，采用虚拟控制格网点进行RPC模型定位精度验证。对已经在第一步中建立的虚拟检查格网点，利用R-D模型和RPC模型分别计算出检查格网点地理坐标对应的图像行列号坐标，比较两种模型的计算结果，评价RPC模型替代R-D模型的可行性。

2.2 RPC模型精化

RPC模型的本质是对传统严格物理模型的高精度拟合，所以，一旦R-D模型存在系统性的几何定位误差，依据其建立的RPC模型也会具有同样的误差[7]。对于SAR影像而言，运动误差、SAR系统误差、地形的影响都会使得影像定位产生偏差，所以需要利用真实地面控制点，对RPC模型进行精化处理，提高几何精纠正的精度。

RPC模型精化一般有两种方法，仿射变换法和有条件的平差方法。以仿射变换法为例[8]：

(4)

其中，(x，y)是真实地面控制点在影像上的量测坐标，(r，c)为根据RPC模型由控制点地理坐标计算得到的SAR影像图像坐标，ei和fi为待求的仿射变换参数。

利用仿射变换进行RPC模型精化的思路是获取一部分GCP(至少3个)，计算出仿射变换参数。当GCP点数≥3，可以解求ei(i=0，1，2)和fi(i=0，1，2)共6个未知参数；当GCP点数=2，可以解求距离向误差系数e2、f2及平移误差系数e0、f0；当GCP点数 = 1，可以只解求e0和f0参数，消除平移误差。

求解得到仿射变换参数后，用另外一部分地面控制点作为独立检查点(Independent Check Point，ICP)来检查精度，通过ICP在影像上量测坐标与其利用精化后的RPC模型参数得到的图像坐标进行比较，实现对精化后的RPC模型精度评估。

2.3 SAR影像几何精纠正

常用几何纠正的方法有基于严格物理模型(如R-D模型)的几何纠正方法、基于通用模型(如RPC模型)的几何纠正法、基于SAR影像模拟的几何纠正方法[9]。3种方法的目的，都是将原始SAR影像从图像坐标系转换到地理坐标系，得到既有SAR影像辐射信息，又有地理参考坐标的正射影像。

本文采用RPC模型对图像进行几何精纠正，在解算出RPC模型参数后，通过计算辅助DEM中每一点对应的SAR影像坐标，然后对SAR影像进行灰度重采样，从而生成一幅正射影像。本文采用双线性插值法对SAR影像灰度进行重采样，同时利用控制点对几何精纠正的精度进行评价。

2.4 几何精纠正精度评定

SAR影像的几何精纠正精度评定可以在纠正后的地图坐标系中进行，通过纠正影像特征与地形图或其他具有精确大地坐标的地面资料进行对比，确定同名地物点在SAR影像上的坐标并量测其在地面上的真实坐标，进而计算纠正影像的几何精度或误差。本文采用的评价纠正精度的定量指标有如下几种。

假设获取了N个用于精度评价的控制点，每一个控制点包含两个二维向量，一个向量Pik[Xi，Yi]表示控制点量测得到的像素坐标或者地理坐标；一个向量Pjk[Xj，Yj]表示经模型计算(如严格物理模

型)或者纠正后影像计算(影像模拟)得到的像素或者地理坐标。K为控制点格式1，2，3，……n。则有：

(1)某个控制点的离散误差，该指标评价的是控制点的离散误差。

Ek=Pik-Pjk(k=1，2，3，……n，以下同)

(6)

(2)最大误差，该指标是控制点中最大误差的量化指标。

Emax=max(Xik-Xjk)

(7)

(3)均方根误差(root mean square error，RMSE)，该指标表明控制点中误差的大小。

(8)

3 实验及分析

3.1 实验数据说明

本文实验区位于中国内蒙古根河地区，实验中采用的是TerraSAR-X和Radarsat-2的两景影像，辅助DEM数据采用的是加密后的ASTER(The Advanced Spaceborne Thermal Emission and Reflection Radiometer)、GDEM(Global Digital Elevation Model)。影像实验区覆盖区域如图1所示。实验中的TerraSAR-X和Radarsat-2的SAR影像数据详细情况如表1所示。

图1 实验区分布图

表1实验区SAR影像数据说明

实验数据TerraSAR-X实验数据Radarsat-2实验数据成像时间2012/09/05 T 9∶41∶5.45132012/09/01 T 9∶47∶35.2401成像模式SL_D(斜距双极化)Fine Quad (精细四极化)数据类型SSCSLC入射角(单位:度)36.805039.4045轨道方向升轨升轨成像方向右视右视地/斜距成像斜距斜距中心经度(单位:度)120.7846329120.7545548中心纬度(单位:度)50.370150650.3540147影像大小(方位向×距离向,单位:m)4684×76745557×3572分辨率(方位向×距离向,单位:m)2.614614×0.9094034.959367×4.733079

实验中DEM数据从NASA卫星数据下载网站(http：//reverb.echo.nasa.gov/)获取。原始DEM分辨率为1弧度(90m左右)，由于根河地区地势较为平坦，可以对DEM数据进行过采样，而不至于原始数据信息大量失真[10]，实验采用的DEM加密到分辨率为0.1弧度(3m左右)。ASTER GDEM的数据详情如表2所示。

3.2 实验区控制点情况

实验区共分布有地面角反射器控制点(Ground Control Point，GCP)22个，控制点分布如图2所示(图中红色标记为控制点)。实验中角反射器的图像坐标采用sinc函数精确提取(图2左上角所示)，角反射器的地理坐标通过在实验测区采用GPS-RTK测量获得(图2右上角所示)。

表2 ASTER GDEM根河地区数据说明

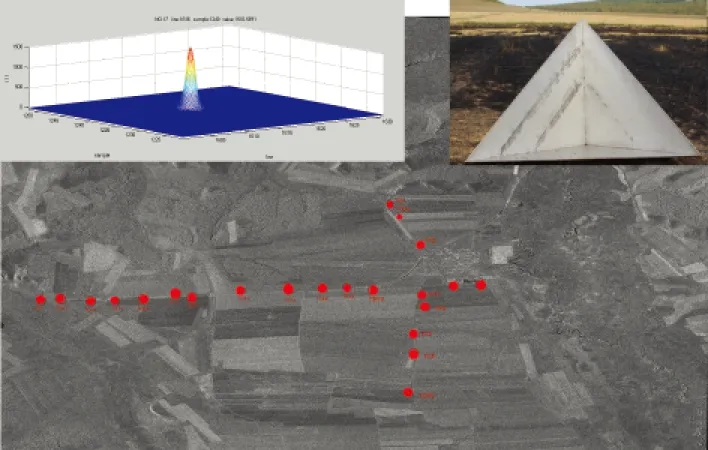
图2 实验区控制点分布图

实验中控制点的作用有3种：①用来验证RPC模型定位；②用以RPC模型精化运算；③几何精纠正的精度结果。首先利用22个角反射器点作为GCP对RPC模型进行初步定位结果精度评价；然后选取其中的11个点作为GCP进行RPC模型精化，其余的11个点作为独立检查点ICP验证精化的结果。在完成基于RPC模型的几何精纠正后，利用上一步的11个GCP和11个ICP来检查正射影像的精度。

3.3 RPC模型定位计算精度评定

3.3.1 检查格网点精度评定

实验中采用了R-D模型生成格网点，定位模型精度评定在SAR图像坐标系下进行，检查格网点的精度评定用于评价RPC模型和R-D模型计算的图像坐标偏差，结果如图3、4所示。

图3表示的是RPC模型的定位精度，其中，图3(a)为TerraSAR-X SAR影像的计算结果，图3(b)为Radarsat-2 SAR影像的计算结果。实验时，控制格网点平面大小为15×15，检查格网点大小为20×20×3，控制点格网高程的层数从4到10层。从图中能够看到，RPC模型对于R-D模型而言，检查格网点的定位误差能够达到10e-6次方以下，即RPC模型能够实现对R-D模型的高精度拟合。

图3 检查格网点精度(单位：像素)

结果表明，相比较于R-D模型，利用虚拟检查格网点验证的RPC模型定位误差小于10e-6像素；说明RPC模型能够实现对R-D模型的高精度地拟合；同时也能发现，高程分层多于4层的时候，RPC模型的精度变化较小，但是由于随着高程层数的增加，参与RPC模型计算的控制点越多，导致算法的计算速度下降。

3.3.2 控制点精度评定结果

由于R-D模型本身可能有误差，导致RPC模型也会产生一定的偏差，所以RPC模型在进行初步的评价精度后，需要利用控制点进行精度评定，评价RPC模型的绝对定位精度。RPC模型精化前的评价精度是在SAR影像的图像坐标系进行的，评价指标为22个GCP的像素坐标和RPC模型计算得到的坐标的误差评定值。

表3为RPC模型在精华前的精度评定结果。可以看出，RPC模型在没有进行模型精化前，Radarsat-2影像在方位向的中误差超过5个像素，而Radarsat-2和TerraSAR影像在距离向的中误差都超过一个像素。通常这是由于SAR影像多普勒估计和轨道偏差所引起的误差大于距离向延迟所带来的误差，所以对于Radarsat-2的SAR影像而言，方位向误差大于距离向误差。TerraSAR-X的轨道精度高，但是X波段受到的延迟较大，所以距离向误差大于方位向误差[11]，TerraSAR影像的距离向定位误差达到了3个像素，而方位向定位误差在子像素范围内。

该结果表明RPC模型精化前，TerraSAR-X与Radarsat-2影像的控制点定位误差均较大，这说明，对于RPC模型而言，尽管能够实现对R-D模型的高精度拟合，但是当R-D定位模型有误差时，由R-D模型提供虚拟控制点解算得到的RPC模型参数也会产生误差。因此，尽管RPC模型参数解算不需要控制点参与，但是当条件允许时，地面控制点需要获取以便对RPC模型进行精化，提高RPC模型的定位精度。

实验中的RPC模型精化是利用22个GCP中的11个作为模型精化点，采用仿射变换，提高RPC模型的定位精度。精化后的精度评价在11个GCP和11个ICP中进行，精度评定结果如表4所示。表4表明，RPC模型经过模型精化后，TerraSAR影像在方位向和距离向的ICP中误差能够控制在百分之一像素范围内；Radarsat-2影像在方位向和距离向的ICP中误差控制在子像素范围。说明RPC模型在定位精度方面具有很高的应用潜力和价值，在有控制点的条件下，精化后的RPC模型能够达到子像素的定位精度。

表3 RPC模型精化前精度评定(控制格网大小为20×20×5)

表4 RPC模型精化后精度评定(控制格网大小为20×20×5)

3.4 正射影像精度评定

在RPC模型精化后，利用RPC模型参数对DEM中的点进行定位计算，并对SAR影像的灰度进行重采样，生成几何精纠正后的正射影像，TerraSAR-X的原始SAR影像如图4(a)所示，正射影像如图4(b)所示；Radarsat-2的原始SAR影像如图5(a)所示，正射影像如图5(b)所示。

图4 TerraSAR-X 原始影像及正射图

图5 Radarsat-2 SAR原始影像及正射图

为了验证正射影像精度，本文采用控制点来进行精度评定，评定指标为正射影像上控制点的地理坐标与其真实地理坐标的偏差(坐标系投影方式为UTM投影，椭球为WGS84)。

图6为正射影像中11个GCP残差和11个ICP的误差分布图。其中，图6(a)为TerraSAR-X SAR影像的正射影像中GCP残差和ICP误差分布情况；图6(b)为Radarsat-2 SAR影像的正射影像中GCP残差和ICP误差分布情况。

TerraSAR-X和Radarsat-2 SAR影像的评价结果如表5所示。其中，TerraSAR-X SAR影像的ICP误差分析中，东西向坐标的中误差为1.501470m，南北向的中误差为1.719557m，平面中误差为2.282825m；Radarsat-2 SAR影像的ICP点东西向坐标的中误差为4.859852m，南北向坐标的中误差为3.620607m，平面中误差为6.060276m。

图6 正射影像控制点误差分布图(单位：m)

表5正射影像控制点的精度评价结果(单位：m)

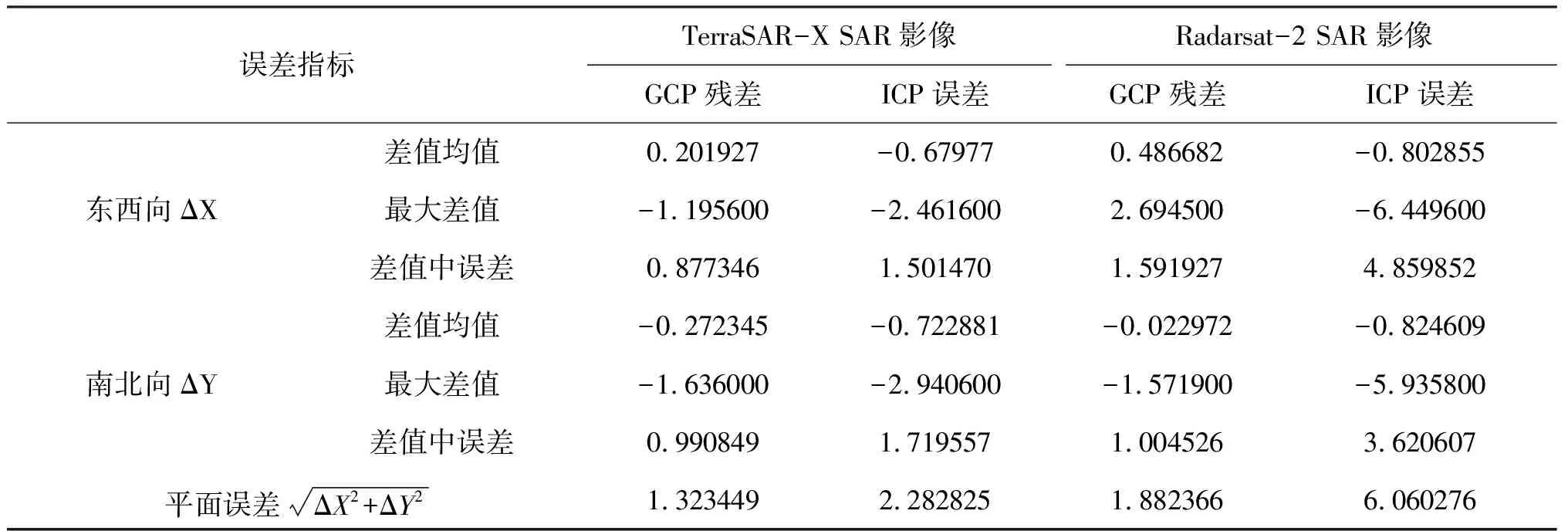
误差指标TerraSAR-X SAR影像Radarsat-2 SAR影像GCP残差ICP误差GCP残差ICP误差东西向ΔX差值均值0.201927-0.679770.486682-0.802855最大差值-1.195600-2.4616002.694500-6.449600差值中误差0.8773461.5014701.5919274.859852南北向ΔY差值均值-0.272345-0.722881-0.022972-0.824609最大差值-1.636000-2.940600-1.571900-5.935800差值中误差0.9908491.7195571.0045263.620607平面误差ΔX2+ΔY21.3234492.2828251.8823666.060276

本文采用的是ASTER GDEM，原始DEM的分辨率为1弧度，过采样率后分辨率为0.1个弧度，约为3m左右。从表5中的结果来看，正射影像的控制点验证精度达到米级，表示RPC模型在几何精纠正方面具有很大的应用价值。由于其运算速度快，无需迭代，所以在模型选择方面具有巨大的效率优势。

4 结束语

SAR影像的几何精纠正对于SAR的应用有着重要的作用。本文将RPC模型进行精化，对RPC精化模型的定位精度进行了评估；发展了一种基于RPC精化模型的SAR影像几何精纠正算法，并利用控制点评价了几何精纠正的精度。结果表明：①相比较于R-D模型，RPC模型的检查格网点精度达到10e-6，说明RPC模型完全能够成为SAR影像的定位模型；②RPC模型参数解算可以不依赖地面实测控制点，利用RD模型生成格网控制点，所以在无控制点的测区，RPC模型具有极大的优势；③RPC模型经过精化后，控制点的定位精度达到百分之一像素级，说明RPC模型在有地面控制点参与模型精化的情况下，能够有效地消除模型可能存在的误差，提高模型定位精度；④基于RPC模型的几何精纠正的精度能够达到米级，且由于R-D模型需要进行迭代运算，耗时较长，RPC模型的算法时间效率大为提高。

SAR影像定位模型的选择主要取决于模型精度和模型运算效率。RPC模型在精度方面能够高精度拟合R-D模型，而且加入控制点进行模型精化后，精度能够达到子像素以下，能够适应实际应用的需求。随着越来越多高分辨率SAR传感器投入使用，基于简单、通用、高效等优点的RPC模型应用将会非常广泛。

参考文献：

[1] 魏晓红，张路，贺雪艳，等.基于有理函数模型的星载SAR影像几何校正[J].遥感学报，2012，16(5)：1090-1100.

[2] FRASER C S，DIAL G，GRODECKI J.Sensor orientation via RPCs[J].ISPRS Journal of Photogrammetry and Remote Sensing，2006，60(3)：182-94.

[3] TAO C V，HU Y.A comprehensive study of the rational function model for photogrammetric processing[J].Photogrammetric Engineering & Remote Sense，Dec 2001，1347-57.

[4] DI K C，MA R J，LI R X.Rational functions and potential for rigorous sensor model recovery[J].Photogrammetric Engineering & Remote Sensing，2003，69(1)：33-41.

[5] 秦绪文，张过，李丽.SAR影像的RPC模型参数求解算法研究[J].成都理工大学学报，2006，33(4)：349-55.

[6] 张过，李德仁，秦绪文，等.基于RPC模型的高分辨率SAR影像正射纠正[J].遥感学报，2008，12(6)：942-948.

[7] ZHANG L，BALZ T，LIAO M S.Satellite SAR geocoding with refined RPC model[J].ISPRS Journal of Photogrammetry and Remote Sensing，2012，69：37-49.

[8] 张剑清，潘励，王树根.摄影测量学[M].武汉：武汉大学出版社，2009.

[9] 宋晶晶.机载SAR影像几何纠正方法研究[D].北京：中国科学院对地观测与数字地球科学中心，2011.

[10] GUINDON B.Development of a SAR data acquisition planning tool (SARPLAN) based on image simulation[J].International Journal of Remote Sensing，1993，14(2)：333-344.

[11] DANKLMAYER A，DORING B，SCHWER-DT M，et al.Assessment of atmospheric propagation effects in SAR images[J].Geoscience and Remote Sensing，IEEE Transactions on，2009，47(10)：3507-3518.