特殊块三对角Toeplitz线性方程组的精化迭代法及收敛性
2019-05-05刘仲云李莉
刘仲云,李莉
(长沙理工大学 数学与统计学院,湖南 长沙,410114)
文中考虑大型稀疏线性方程组
Ax=b
(1)
的迭代解法,其中x,b∈Rn,A∈Rn×n为含Toeplitz块的全正块三对角随机Toeplitz矩阵,即A有如下结构:
其中:Ti(i=-1,0,1)为Toeplitz矩阵[1]。
一个非奇异矩阵称为全正矩阵[2],如果它所有的子式都是非负的。
一个矩阵是一个随机矩阵,如果它是非负矩阵且每一行的行和都为1。
这类线性方程组频繁出现在三次均匀B样条曲面拟合及二阶微分方程数值解等问题中。
1 精化迭代法
求解(1)式的精化迭代法的迭代格式为
x(k+1)=x(k)+d(k)
(2)
Ad(k)=r(k),r(k)=b-Ax(k)
(3)
其中:x(0)为初始迭代向量,k=0,1,…
当d(k)为(3)的精确解时,迭代格式(2-3)退化为单步迭代精化。不难看出,该迭代格式可以提高解x(k)的精度[3]。另外,倘若用高精度方法求解(3),则迭代格式(2-3)为迭代精化[4-5],把该迭代格式称为精化迭代法。
引理1 假设不考虑舍入误差,精确计算残差r(k),d(k)为(3)的精确解,则x(k+1)为(1)的精确解。
证明 由(3)式知Ad(k)=r(k),r(k)=b-Ax(k),从而Ax(k+1)=Ax(k)+Ad(k)=b。这意味着x(k+1)是(1)的精确解,证毕。
由于A的正定性,因此,用广义极小残差法(GMRES)非精确求解(3),这样就得到精化迭代法的基本框架。
设d(k,l)为用GMRES方法求解(3)得到的第l个近似解,其中,初始迭代向量d(k,0)=0,终止检验公式为
(4)
其中:τk是终止判别。
倘若d(k,Lk)满足终止检验公式(4),从而
x(k+1)=x(k)+d(k,Lk)
(5)
通常,为了确保计算效率,(5)的终止检验公式为
‖r(k+1)‖≥θ‖r(k)‖,θ∈[0,1]。
(6)
为方便算法实现,将精化迭代法每次迭代的具体步骤总结为下面的流程图(见下图1)。

输入初始迭代向量x(0),终止判别τk和精度θ。 Step 1.计算残差r(k); Step 2.利用GMERES方法求解Ad(k)=r(k),寻找满足终止检验公式(4)的d(k,Lk); Step 3.更新x(k+1)=x(k)+d(k,Lk); Step 4.若满足终止检验公式(6),则输出近似解x(k+1),计算结束;否则,令 x(k)=x(k+1),k=k+1,转Step 1。
图1精化迭代法每次迭代的具体步骤
Fig.1Specific steps of each iteration of the refined iterative method
显然,对于不同的τk值,d(k,Lk)不同,精化迭代法的收敛速度也不同。当τk等于0时,可以把算法1得到的解认为是公式(1)的精确解。因此,当选取的τk值较小时,迭代序列有较好的收敛速度。
定理2 令x*为线性方程组(1)的精确解。对第k步迭代,用GMRES方法求解(3)的初始迭代向量均为d(k,0)=0,相应的迭代序列为{d(k,l)}Lkl=0且d(k,Lk)满足终止检验公式(4),则迭代序列{x(k)}k=0满足
‖x(k+1)-x*‖≤τkκ(A)‖x(k)-x*‖,
其中:κ(A)=‖A‖·‖A-1‖。
特别地,当
ηmax=τmaxκ(A)<1,
迭代序列{x(k)}k=1收敛到x*,其中
证明 由(4)式知
x(k+1)-x*=x(k)-x*+d(k,Lk)=
A-1[Ad(k,Lk)-rk],
从而
‖x(k+1)-x*‖≤‖A-1‖‖Ad(k,Lk)-rk‖≤τk‖A-1‖‖rk‖≤
τk‖A-1‖·‖A‖·‖x(k)-x*‖=τkκ(A)‖x(k)-x*‖≤ηmax‖x(k)-x*‖。
当ηmax<1时,迭代序列{x(k)}k=1收敛,证毕。
2 数值实验
下面给出精化迭代法应用于曲面拟合的两个例子。采用三次均匀B样条曲面插值相应的数据点,利用精化迭代法求相应的控制点,从而得到插值给定点集的曲面。第k步迭代得到的三次均匀B样条曲面的拟合误差计算式为
右端向量b等于数据点{Pij}(i=0,1,…,m;j=0,1,…,n),系数矩阵均为A=B1⊗B2,符号⊗表示Kronecker积,其中B1∈Rm×m,B2∈Rn×n为配置矩阵,形如
例1 利用三次均匀B样条曲面逼近peak函数

中的点
例2 利用三次均匀B样条曲面逼近
中的点
利用三次均匀B样条曲面迭代逼近例1、2中的点。所有的数值实验是在Matlab7.4.0.287(R2014a)环境中实现。在数值实验中,取τk=10-2,ε=10-8。为了比较,还测试了文献[6]中加权渐进迭代逼近法(WPIA)。表1、2给出了系数矩阵的阶数不同时,三次均匀B样条曲面的精化迭代法和WPIA逼近例1、2中的点所需迭代次数和计算时间。
表1 精化迭代法与加权渐进迭代逼近法求解例1
Table 1 Comparisons between the refined iterative method and WPIA for Case 1
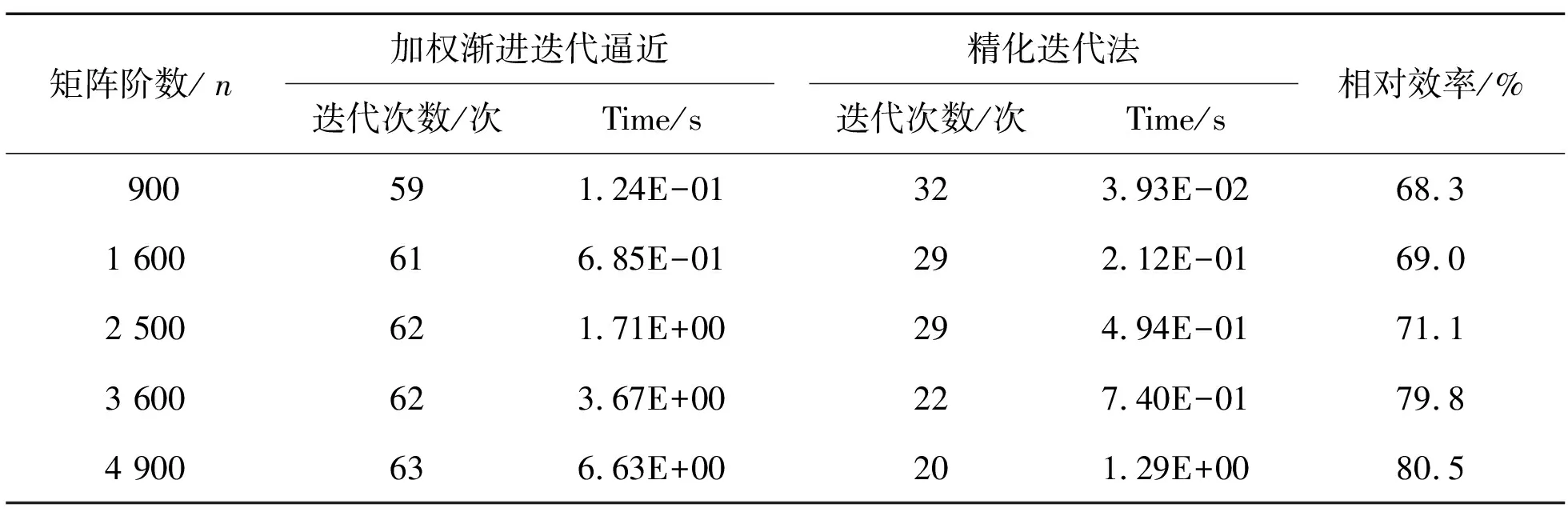
矩阵阶数/n加权渐进迭代逼近迭代次数/次Time/s精化迭代法迭代次数/次Time/s相对效率/%900591.24E-01323.93E-0268.31 600616.85E-01292.12E-0169.02 500621.71E+00294.94E-0171.13 600623.67E+00227.40E-0179.84 900636.63E+00201.29E+0080.5
表2 精化迭代法与加权渐进迭代逼近法求解例2
Table 2 Comparisons between the refined iterative method and WPIA for Case 2
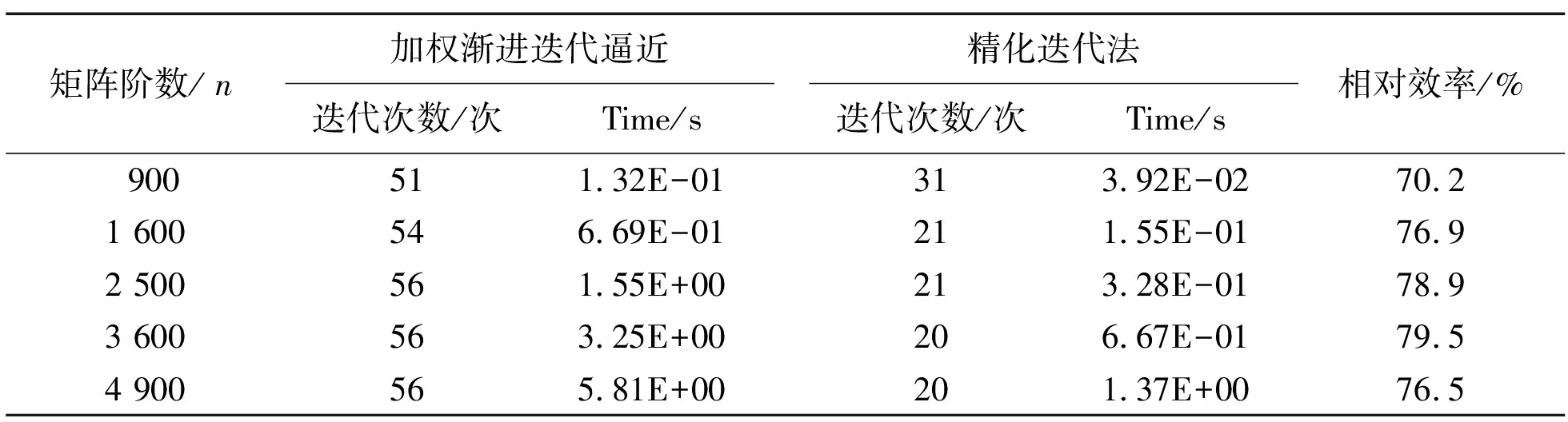
矩阵阶数/n加权渐进迭代逼近迭代次数/次Time/s精化迭代法迭代次数/次Time/s相对效率/%900511.32E-01313.92E-0270.21 600546.69E-01211.55E-0176.92 500561.55E+00213.28E-0178.93 600563.25E+00206.67E-0179.54 900565.81E+00201.37E+0076.5
在表1、2中,n为系数矩阵A的阶数;Time为单独计算100次的平均计算时间,相对效率计算公式为
其中:tw为加权渐进迭代逼近法的计算时间;tr为精化迭代法的计算时间。
由表1、2可看出,在迭代次数和计算时间上,精化迭代法都要优于加权渐进迭代逼近法,且矩阵规模越大,优势就愈明显。
