基于ICP算法的非常规航空影像与机载LiDAR数据配准

杜全叶，麦晓明，褚福侠，彭向阳，王锐

(1.中国测绘科学研究院，北京 100830；2.广东电网公司电力科学研究院，广州 510080；3.济宁光大房地产服务有限责任公司，济宁 272000)

1 引 言

随着机载激光扫描(LiDAR)技术推广使用，短时间内可以获取大范围地面离散点的三维坐标。航空影像在地表纹理表达上有着不言而喻的明显优势。航空影像与机载LiDAR数据配准，有利于发挥两种数据的优势，为建模和纹理映射等应用，打下良好的基础。

如何配准激光扫描数据和对应的光学影像，很多学者都做过一些研究。Habbib使用LiDAR和影像数据上人字形房屋顶交线作为配准的基元，将这些直线特征的点坐标代入变换函数，利用最小二乘原理解算出配准参数[1]。吴波利用影像的平面特征和LiDAR数据中的离散点作为配准的基元[2]，配准航空影像和机载LiDAR数据。Mwafag Ghanma在其博士论文中，讨论了基于直线段和面片的航空影像与LiDAR数据的配准[3]。这些配准方法局限于有直线特征或平面特征的区域。

航空摄影测量一般需按航空摄影规范进行航线的设计，然后按预设的航线进行飞行和影像获取。但是在发生地震、滑坡等自然灾害的应急响应中，为了第一时间获取通往灾区的主要道路、桥梁等交通设施的毁坏情况，及时地为救援行动提供决策参考，就必须进行“非常规”的航空摄影，即沿着主要的道路进行飞行[4]。使用机载激光扫描设备和数码成像设备同时进行常规作业时，也可能会因相机像幅不大，视场角相对激光扫描仪的视场角小，而造成影像重叠度达不到53%。这些非常规航空影像无法进行传统的区域网空中三角测量，它们与机载LiDAR数据的配准更加困难。

2 原理和方法

利用摄影测量中的共线方程[5]描述配准后的LiDAR点和影像的对应关系，即配准后LiDAR脚点，影像上对应的像点，以及摄影中心在同一条直线上。此时，配准航空影像与LiDAR数据，即转化为求解影像在LiDAR坐标系下方位元素的问题。首先，航空影像上提取密集特征点，在LiDAR点云和定位定向系统(Position and Orientation System，POS)数据辅助下，利用匹配和前方交会得到匹配点云，然后配准匹配点云与LiDAR点云，最后，筛选良好的配准点解算出影像方位元素，实现影像与LiDAR数据配准，流程如图1所示。

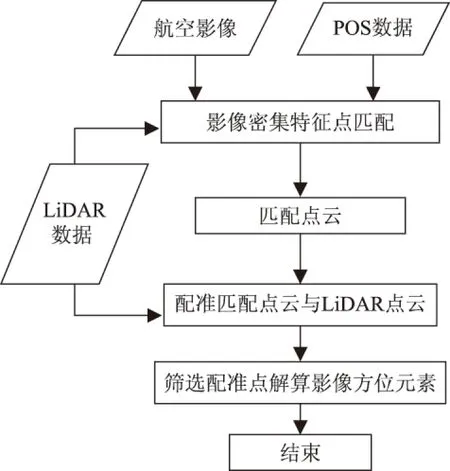
图1 航空影像与LiDAR数据配准流程

航空影像需要有全球定位系统(Global Positioning System，GPS)和IMU测量的POS数据作为影像的初始外方位元素，若没有POS数据，则需要人工选取影像与LiDAR数据的同名点，解算影像初始方位元素。

2.1 影像匹配

采用立体像对密集匹配方式获得影像匹配点云。如图2所示，航摄区域连续影像，前4张标记为Photo1、Photo2、Photo3和Photo4，斜线区域为相邻影像重叠区。

图2 立体像对密集匹配示意图

首先，在每张影像上提取密集Harris特征点。然后，将Photo1与Photo2在LiDAR点云生成的数字表面模型(Digital Surface Model，DSM)和POS数据辅助下进行特征点匹配，得到两张影像匹配点云——“Photo1-Photo2匹配点云”，将Photo2与Photo3进行特征点匹配，得到“Photo2-Photo3匹配点云”，以此类推。

2.2 点云配准

计算机视觉界已经对三维离散点云的拼接做了大量的研究工作，最常用的点云拼接方法是1992年由Besl教授提出的迭代最临近点算法(ICP，Iterative Closest Point)[6]。它是一个寻找两个三维表面点集，最优匹配几何变换的迭代优化过程。目的是确定相邻两个坐标系之间的转换参数F，包括旋转矩阵R和平移向量T，以使得位于坐标系1中的点P与位于坐标系2中的点Q重合，即FP=Q，表达成R和T函数关系式即为RP+T=Q。P与Q不可能完全重合，因此，该问题就转化为寻找参数F，使得|FP-Q|*|FP-Q|的值最小。具体实现是通过迭代的方法找到均方差最小的变换。具体步骤如下：

①k为第k次迭代，旋转参数Rk和平移参数Tk，Pk和Qk分别代表参与计算的两个点集，那么两个点集的函数关系式为RkPk+Tk=Qk，初始化k=0。

②寻找Pk中对应的每个最近点Qk(k为第k次迭代)；

③寻找互换最邻近点Pεk和Qεk(同时互为最近点且距离小于ε时才被标注)；

④解算Pεk和Qεk间的均方距离dk(Pεk和Qεk是第k次迭代中互换的最邻近点)；

⑤解算Pε0和Qεk间最小二乘意义下的三维变换参数Rk、Tk；

⑥执行变换：Qk+1=RkPεk+Tk；

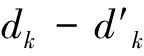
目前，地面激光扫描点云拼接，机载LiDAR数据的拼接和星载LiDAR数据的拼接都应用此算法。本文也将ICP算法应用于密集匹配点云与LiDAR点云的配准。ICP算法中所要求的初值，由影像初始方位元素确定。

2.3 单像空间后方交会

单像空间后方交会是利用控制点及其相应的像点求解航片外方位元素。本文筛选点云配准后距离小于平均LiDAR点间隔的配准点作为控制，采用基于单位四元数的方法进行单像空间后方交会[7]。基本思路为：先求出摄站点与控制点的距离；然后利用单位四元数表示旋转，从而获得旋转矩阵，得到外方位元素；最后再求出摄站点的坐标。这种方法不需要对共线条件方程进行线性化，且无需提供外方位元素初值，计算简便，对于大倾角摄影的航片也能适用。

图2中重叠区域的匹配点云分别与对应的LiDAR数据配准后，筛选良好的配准点，利用单像空间后方交会解算出影像Photo2、Photo3等的方位元素，实现航空影像与LiDAR数据的配准。Photo1影像上仅右边有少部分配准点，必要时也可后方交会解算其方位元素。

3 配准实验一

3.1 实验数据

实验数据为使用Leica ALS50-II获取的某平原区LiDAR数据和随带RCD105数码相机拍摄的航空影像，航高为500m，影像重叠度约为20%。影像像幅为7162×5389像素，像元大小为0.0068mm，影像地面分辨率为0.1m，平均LiDAR点间隔为0.4m。以连续4张影像和对应的LiDAR数据为实验对象。

3.2 人工配准

从影像和对应的LiDAR点云数据中手工选取9个同名点，获得同名点像坐标和物方坐标，经过单像空间后方交会获得影像外方位元素。第二张和第三张影像手工配准过程中，后方交会中误差(Root Mean Square Error，RMSE)如表1所示。

3.3 影像密集匹配

自动配准过程中，相邻两张影像密集匹配获得的匹配点云如图3所示。

表1 手工配准后方交会中误差

图3 影像立体匹配点云

密集匹配点使用影像初始方位元素前方交会出点的物方三维坐标。相邻两张影像重叠度不大，一个像对仅匹配出单张影像上20%左右的密集点云。

3.4 点云配准结果

影像匹配点云与LiDAR点云配准中误差如表2所示。影像匹配点云与LiDAR点云配准后，Photo2和Photo3单像空间后方交会中误差如表3所示。

表2 点云配准中误差

表3 后方交会中误差

3.5 配准后点云投影结果

配准之后，选择LiDAR点云数据中的一些平顶房房顶点云，投影到对应影像上检查配准效果。其中一个房顶点云数据如图4中红色区域所示。

图4 LiDAR点云中的屋顶数据

第2张影像和第3张影像中，配准前后其中一个屋顶数据的投影结果如图5、图6、图7和图8所示。

图5 Photo2影像配准前点云投影结果

图6 Photo2影像配准后点云投影结果

图7 Photo3影像上配准前点云投影结果

图8 Photo3影像上配准后点云投影结果

其中，红色点为LiDAR脚点投影到影像上的位置。从图中可以明显看出，在配准后房屋的错位现象已经消除，航空影像与LiDAR数据已经配准好。

4 配准实验二

4.1 实验数据

如同实验一，只是相邻影像重叠度增大，约为60%。

4.2 密集匹配结果

连续3张影像进行立体像对密集匹配，经过前方交会生成的点云如图9所示。

图9 影像立体匹配点云

4.3 点云配准结果

密集匹配点云与LiDAR点云配准中误差如表4所示。影像匹配点云与LiDAR点云配准后，Photo2影像后方交会中误差为0.005114mm。

表4 点云配准中误差

5 实验分析

从Photo2影像对应的LiDAR数据中选取房屋屋顶数据，按照配准前方位元素、手工配准后方位元素和通过点云配准后的方位元素，投影到影像上，如图10、图11和图12所示。

通过对比可以看出，配准前LiDAR点云投影到影像上有较大错位，人工配准的方式，已经消除了错位现象，LiDAR点投影到影像上后误差在一个LiDAR点间距以内，而通过匹配点云配准后屋顶的LiDAR点投影到影像后误差更小，航空影像与LiDAR数据配准的精度更高。

图10 配准前屋顶LiDAR点投影结果

图11 人工配准后屋顶LiDAR点投影结果

图12 自动配准后屋顶LiDAR点投影结果

通过表1手工配准后方交会中误差和表 3 后方交会中误差(点云配准方式)对比，可以看出，采用手工配准的方式一般情况下可以达到影像的4个像素，也就是一个LiDAR点间隔的精度。而采用影像匹配点云配准的方式即便只有20%的重叠度的情况下也能达到影像4个像素以内，良好情况下达到2个像素的精度，即半个LiDAR点间隔的精度。如果重叠度达到60%，那么点云配准的精度会更高，解算的影像方位元素精度可以到达1个像素以内。

6 结束语

通过影像匹配点云和LiDAR点云配准，然后利用配准点后方交会解算影像方位元素的配准方法，相对于手工配准航空影像和机载LiDAR数据，自动化程度大大提高，并且达到的精度也更高。这种方法对于解决非常规摄影测量的航空影像与LiDAR数据的自动高精度配准非常有效，也适用于重叠度更大的常规航空影像。

参考文献：

[1] HABIB A F，SHIN S，KIM C，et al.Integration of Photogrammetric and LIDAR Data in a Multi-Primitive Triangulation Environment[J].Innovations in 3D Geo Information Systems，2006：29-45.

[2] 吴波.自适应三角形约束下的立体影像可靠匹配方法[D].武汉：武汉大学博士学位论文，2006.

[3] GHANMA M.Integration of photogrammetry and LIDAR[D].Calgary：Universityof Calgary (Canada).Ph.D.dissertation，2006.

[4] 张祖勋，郭大海，柯涛，等.抗震救灾中航空摄影测量的应急响应[J].遥感学报，2008，12(6)：852-857.

[5] 王之卓.摄影测量原理[M].武汉：武汉大学出版社，2007.20-21.

[6] BESL P J，MCKAY N D.A method for registration of 3-D shapes[J]，IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14(2)：239-256.

[7] 官云兰，程效军，周世健，等.基于单位四元数的空间后方交会解算[J].测绘学报，2008，37(1)：30-35.