基于弱交叉克尔非线性的多粒子GHZ态融合

2014-08-01熊标朱晓慧于昌本计新

延边大学学报（自然科学版） 2014年3期

熊标,朱晓慧,于昌本,计新

(延边大学理学院物理系，吉林延吉 133002)

0 引言

量子信息学是利用量子力学基本原理重构数值计算和信息处理方法的一门新学科，在量子信息处理中最核心的物理基础为量子纠缠.目前为止，人们已经从理论上提出了很多不同种类的量子纠缠态，如Bell态、GHZ态、W态和团簇态等，并且已经在许多不同物理系统中实现了纠缠态的制备[1-4].研究发现，GHZ态不仅是量子纠缠交换、量子隐形传送中进行量子密钥分配和秘密共享的重要通道，而且还可以用于验证量子力学与定域实在论的矛盾；因此，很多学者都十分关注GHZ态的制备与应用.1999年，潘建伟和Bouwmeester等人首次在实验上制备了3个粒子的纠缠[5-6]，2000年他们又制备了4粒子的纠缠[7]，但是这些实验方案都是概率性的.此外，虽然对5光子等多粒子纠缠的制备及操作的方案在理论上非常明确，但是由于光子之间难以发生相互作用，且仅由线性光学元件构成的逻辑门的实现概率较低，因此它在实验上非常难以实现.

在实际中，人们往往都会涉及到多粒子信息的处理，因此实现多粒子GHZ态的融合也受到研究者的广泛关注.2005年，Browne等[8]提出了线性光学量子计算的方案，利用几对线性光学元件制备了高偏振光子间的纠缠态,并给出了制备多粒子纠缠态的方法；随后，Bugu等[9]利用Fredkin门，在辅助光子的帮助下有效地提高了多粒子W态融合的成功概率.以上这些方案虽然都能较好地实现多粒子纠缠态的融合，但是研究者在方案中都没能够充分地利用系统的物理资源(部分比特被探测掉)，并且方案的融合成功概率也没能达到1.1985年，Imoto等[10]利用在克尔介质中发生的交叉相位调制提出了光子数的量子非破坏性测量方案；文献[11-12]通过强的相干光来补偿弱的非线性,并结合经典前反馈,提出了在弱交叉克尔效应条件下实验上可行的非破坏性光子数区分探测器.受这些文章的启发，本文在光学系统下利用简单的线性光学元件结合弱交叉克尔非线性介质，辅以适当的探测手段实现了两个多粒子GHZ态的充分融合；此外，利用经典反馈，使方案的成功概率有效地提升至1.

1 多粒子GHZ态融合

为实现两个多粒子GHZ态的融合，首先考虑两个参与者Alice和Bob，他们分别拥有n光子的|GHZA〉n态和m光子的|GHZB〉m态，并且Alice可以精确地操控其拥有的第n个光子，而Bob可以精确地操控其拥有的m个光子.Alice和Bob拥有的纠缠态的具体形式为：

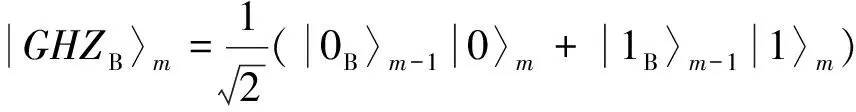
(1)

其中：|iA〉n-1=|i〉1⊗|i〉2⊗…⊗|i〉n-1,i=0,1，表示Alice的前n-1比特都处于量子态|i〉上； |iB〉m-1=|i〉1⊗|i〉2⊗…⊗|i〉m-1，i=0,1，表示Bob的前m-1比特都处于量子态|i〉上.

图1 两量子比特偏振量子非破坏探测器示意图(PBS代表极化分束器)

|0A〉n-1|1B〉m-1|0〉n|1〉m+|1A〉n-1|0B〉m-1|1〉n|0〉m+|1A〉n-1|1B〉m-1|1〉n|1〉m)|αc〉.

(2)

当光子通过PBS2和PBS4后，联合系统的量子态演化为

|0A〉n-1|1B〉m-1|0〉n|1〉m|αcei θ〉+|1A〉n-1|0B〉m-1|1〉n|0〉m|αce-i θ〉=

|0A〉n-1|1B〉m-1|0〉n|1〉m|αcei θ〉+|1A〉n-1|0B〉m-1|1〉n|0〉m|αce-i θ〉.

(3)

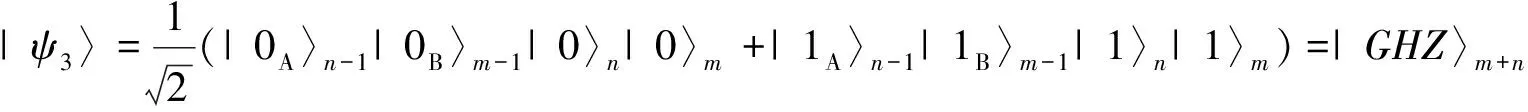
(4)

由此成功地实现两个GHZ态的融合.如果测量结果为|ace±i θ〉，则将获得如下的量子态：

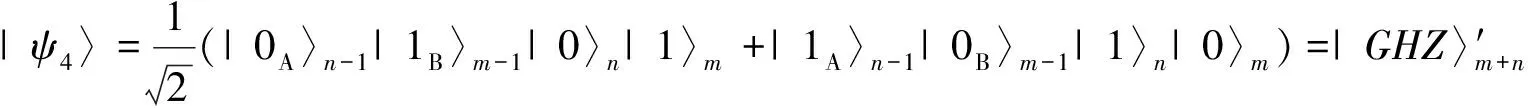
(5)

虽然这个量子态也是GHZ态，但它与常用的编码习惯有差别，因此视之为融合失败.至此，本文的融合方案的整体成功率为0.5.

为提高其融合效率，我们施加经典反馈，如图2所示.该反馈调节机制将|ψ4〉中Bob拥有的m个比特进行φ(X)操作，并且将φ(X)特殊化为比特反转操作，即将|ψB〉j(j=1,2,3，…，m)中的|1〉态变为|0〉态，将|0〉态变为|1〉态.施加经典反馈后系统的末态为

(6)

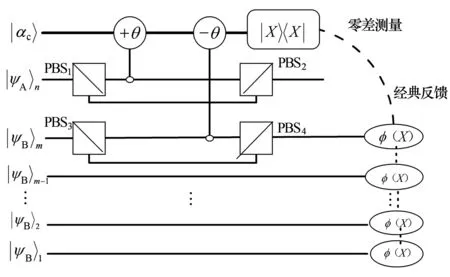
图2 结合经典反馈的CHZ态融合装置图

由此将融合失败的量子态变为本文所要的多粒子GHZ态，融合成功率提高至1.

由于在方案中需要用到X正交分量零差测量[13]，所以有必要考虑该测量的误差率：

(7)

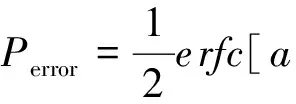
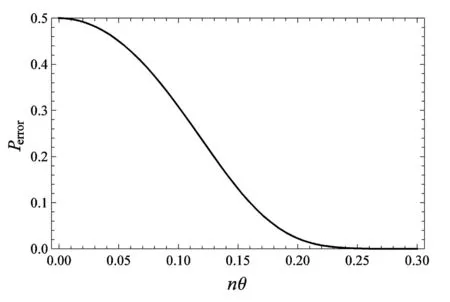
图3 a=100时Perror随nθ的变化趋势图

2 结论

本文利用弱交叉克尔非线性在光学系统中实现了两个GHZ态的多粒子融合.通过结合经典反馈将GHZ态融合的成功率从50%提高到100%.此外，本文的方案也可以在其他物理系统中实现，例如腔量子电动力学系统、离子阱系统等，只需将文中的宇称门进行适当的改变，再辅以适当的探测即可.

参考文献：

[1]Sackett C A,Kielpinski D,King B E,et al. Experimental entanglement of four particles[J]. Nature (London),2000,404:256-259.

[2]Rauschenbeutel A,Nogues G,Osnaghi S,et al. Step-by-step engineered multiparticle entanglement[J]. Science,2000,288:2024-2028.

[3]Pan J W,Daniell M,Gasparoni S,et al. Experimental demonstration of four-photon entanglement and high-fidelity teleportation[J]. Phys Rev Lett,2001,86(20):4435-4438.

[4]Yao X C,Wang T X,Xu P,et al. Observation of eight-photon entanglement[J]. Nature Photonics,2012,6:225-228.

[5]Pan J W,Bouwmeester D,Daniell M,et al. Experimental test of quantum non-locality in three-photon Greenberger-Horne-Zeilinger entanglement[J]. Nature,2000,403:515-519.

[6]Zeilinger A,Horne M A,Weinfurter H,et al. Three-particle entanglements from two entangled pairs[J]. Phys Rev Lett,1997,78:3031-3034.

[7]Sackett C A,Kielpinski D,King B E,et al. Experimental entanglement of four particles[J]. Nature,2000,404:256-259.

[8]Browne D E,Rudolph T. Resource-efficient linear optical quantum computation[J]. Phys Rev Lett,2005,95(1):010501.

[9]Bugu S,Yesilyurt C,Ozaydin F. Enhancing the W-state quantum-network-fusion process with a single Fredkin gate[J]. Phys Rev A,2013,87(3):032331.

[10]Imoto N,Haus H A,Yamamoto Y. Quantum nondemolition measurement of the photon number via the optical Kerr effect[J]. Phys Rev A,1985,32(4):2287-2292.

[11]Munro W J,Nemoto K,Spiller T P,et al. Efficient optical quantum information processing[J]. Journal of Optics B: Quantum and Semiclassical Optics,2005,7(7):S135-S140.

[12]Nemoto K,Munro W J. Nearly deterministic linear optical controlled-NOT gate[J]. Phys Rev Lett,2004,93(25):250502.

[13]Pittman T B,Jacobs B C,Franson J D. Probabilistic quantum logic operations using polarizing beam splitters[J]. Phys Rev A,2001,64(6):062311.