一个二维含有理分式离散混沌映射的分析与控制
2014-08-01彭建奎俞建宁张莉
彭建奎,俞建宁,张莉
(1.兰州文理学院 师范学院,甘肃 兰州 730010; 2.兰州交通大学 数理学院,甘肃 兰州 730070;3.兰州工业学院 基础部,甘肃 兰州 730050)
混沌研究是数学和物理学等学科的研究热点之一,由于混沌系统具有极其复杂性和对初始值的敏感性,因此混沌在通信保密等领域得到了很好的应用[1-3].研究者在对混沌产生机理进行研究时发现,有些混沌运动会对系统本身产生严重危害,甚至会导致灾难性后果[4],因此混沌控制成为混沌研究领域的一个重要研究方向.文献[4-6]提出了许多混沌控制方法,但这些混沌控制方法并没形成较系统的控制理论.
对于实际系统而言,如何设计一种既简单又快速达到混沌控制目的的控制器是研究混沌控制的重要方向.快速衰减性是小波函数的特点之一,文献[7]表明采用小波函数构造的非线性压缩映射具有更有效的控制能力,使混沌系统能够得到快速而有效的控制.含有理分式离散映射比一般离散映射具有更丰富的动力学行为[8],该映射在参数取适当值时处于混沌状态,映射具有3个凹凸区域并含一个峰值.本文作者在分析含有理分式的一维映射动力学[9]时发现,该映射产生混沌道路是倍周期分岔通向混沌的过程.本文在此研究基础上构造了一个二维含有理分式离散系统,并对其动力学行为和控制结果进行了分析和验证.
1 一维含有理分式离散映射模型
一个含有理分式离散映射的数学模型[8]描述为
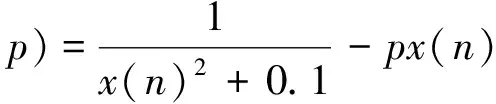
(1)
其中参数p∈[-0.990,0.990],x∈[-10.002 5,10.002 5].当参数p在[-0.999 0,0.999 0]时发生变化,其系统对应的Lyapunov指数谱与分岔图如图1和图2所示,由此可知,当p∈[0.07,0.15]∪[0.25,0.35]∪[0.38,0.51]∪[0.57,0.62]∪[0.64,0.67]时,Lypunov指数λ>0,即离散系统(1)处于混沌状态.
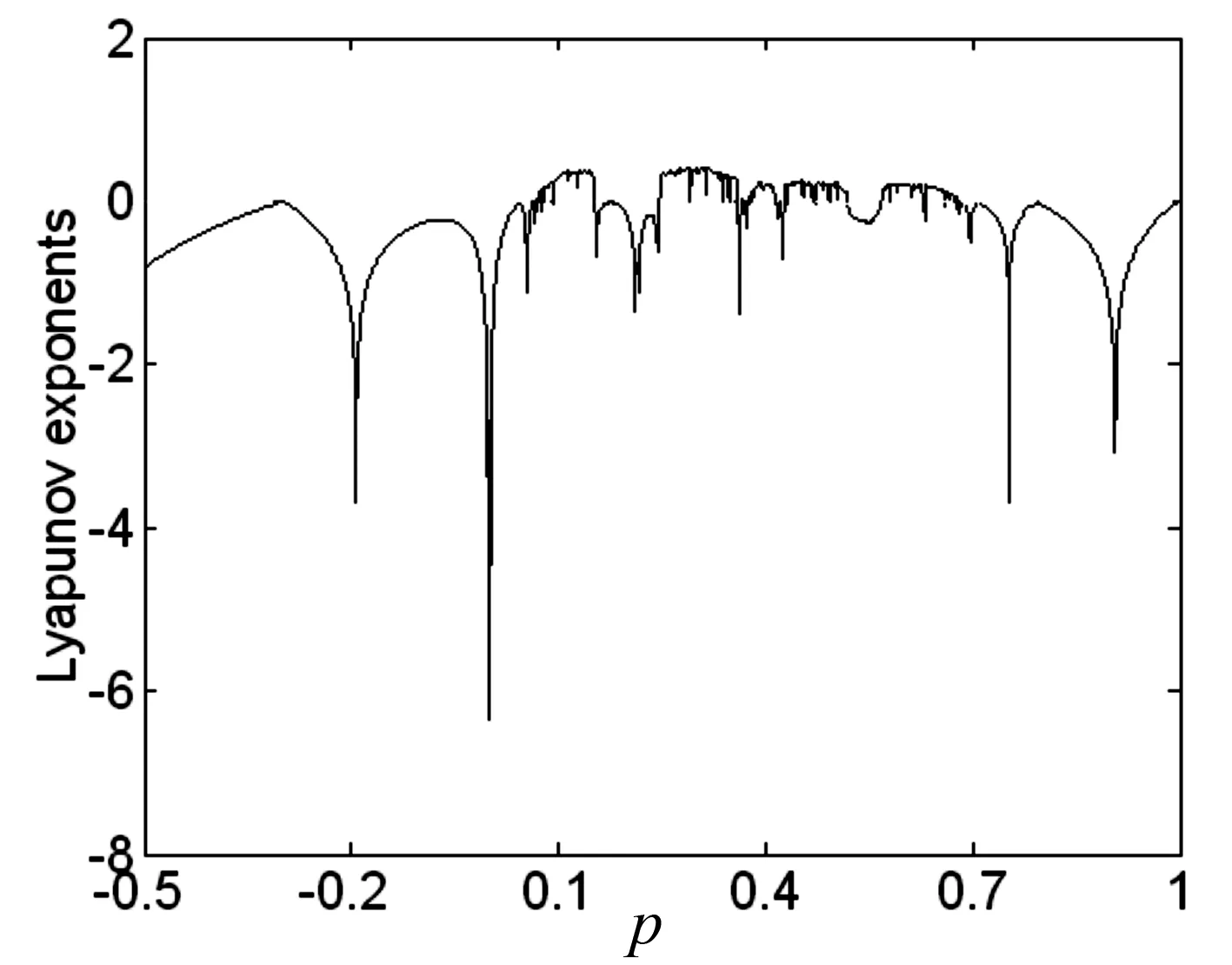
图1 一维离散映射Lyapunov指数谱

图2 一维离散映射全局分岔图
2 二维含有理分式离散系统模型的动力学分析
2.1 基于修正的Marotto定理的混沌分析
2005年,陈关荣[10]指出了Marotto定理中的错误,并给出了Marotto定理的修正定理:
现根据含有理分式的一维离散映射的研究,给出二维含有理分式的离散映射:
(2)
其中g1(xn,yn),g2(xn,yn)为耦合项.选取对称二次耦合项g1(xn,yn)=g2(xn,yn)=rxnyn,即得具有对称二次耦合项的二维有理分式的离散系统模型
(3)
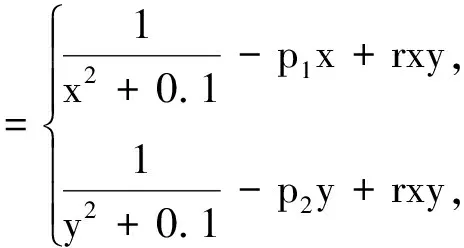
定理2在系统(3)中,选择参数p1=p2=0.5,r=0.11,则系统(3)的不动点是映射f的返回扩张不动点,即系统(3)在Li-Yorke意义下是混沌的.
证明运用Matlab软件容易得到系统(3)的不动点,其中一个不动点为O1(13.632 8,13.632 8),其雅可比矩阵为


根据定理1,若x0∈Bq(O1)使f在x0某领域内连续可微并满足detDf(x0)≠0,detDf(x1)≠0,则不动点O1为f的返回扩张不动点,并且可直接验证detDf(x0)=0.625 2≠0,detDf(x1)=-19.710 3≠0.
通过以上证明可知映射系统(3)在Li-Yorke意义下是混沌的.
2.2 二维含有理分式离散系统混沌道路的数值仿真
Lyapunov指数是衡量系统动力学特性的一个重要定量指标.当p1=p2=0.5,r∈[-0.1,0.15]和r∈[0.3,0.5]时,运用全局分岔图和最大Lyapunov指数谱,研究该二维有理分式离散映射动力学行为演化过程表明,随着r的增大,该二维含有理分式离散映射通过倒倍周期分岔通向混沌道路,并具有比一维含有理分式离散映射更加丰富的动力学行为(图3).
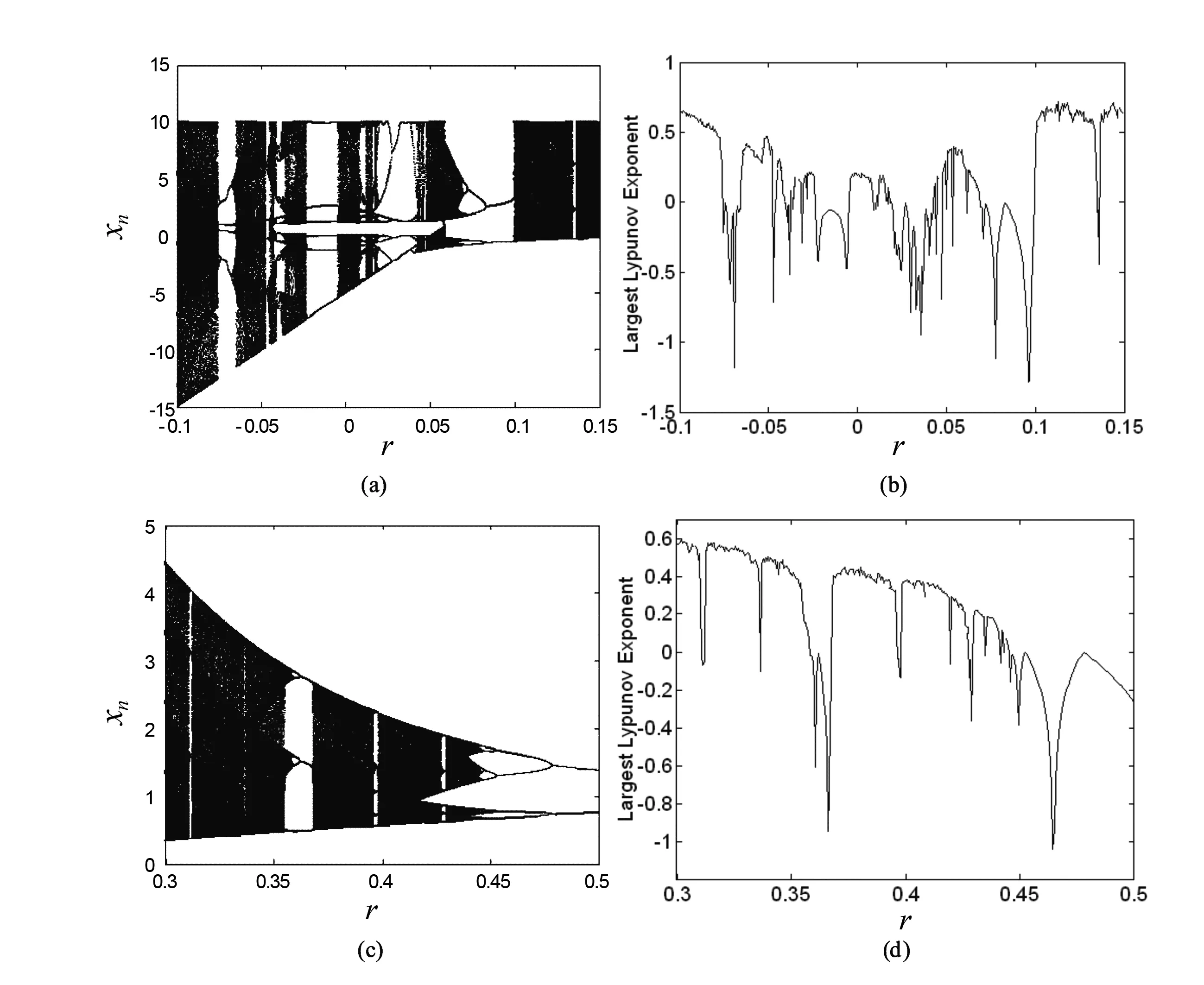
图3 系统映射随参数r变化的全局分岔图和最大Lyapunov指数谱
当r=0.11,p1=p2=p,p∈[-0.5,0.8]时,运用全局分岔图和最大Lyapunov指数谱,研究该二维有理分式离散系统动力学行为演化过程表明,随着p的增大,该二维含有理分式离散映射通过倍周期分岔通向混沌道路(图4).
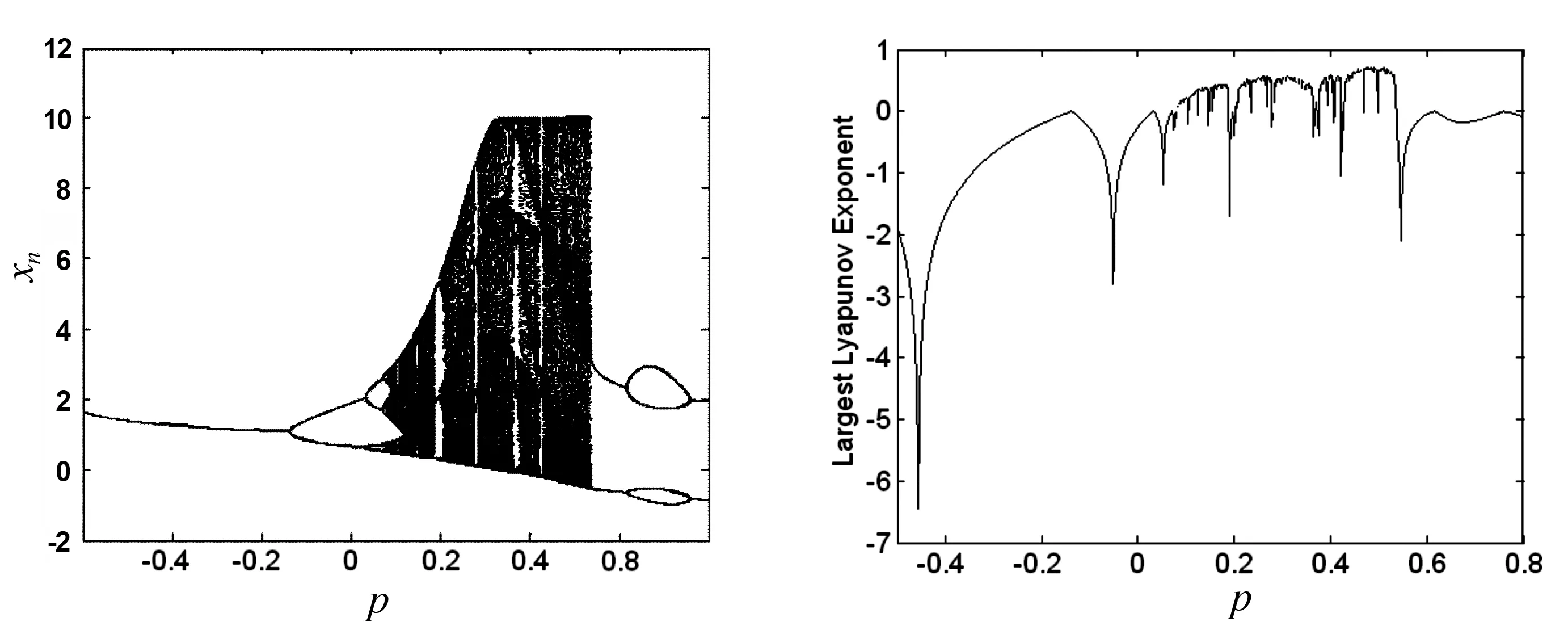
图4 系统映射随参数p变化的全局分岔图和最大Lyapunov指数谱
3 二维含有理分式离散系统的混沌控制
3.1 小波函数变换控制法思想
文献[7]指出小波变换可以控制系统的混沌,小波函数所构造的非线性映射法简单,只需设置一个控制开关,并且该构造方法可对所构造的压缩映射进行改进,将压缩映射施加于多个变量,使混沌系统得到更有效的控制.


(4)
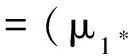
3.2 混沌控制的数值仿真
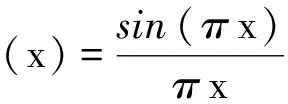
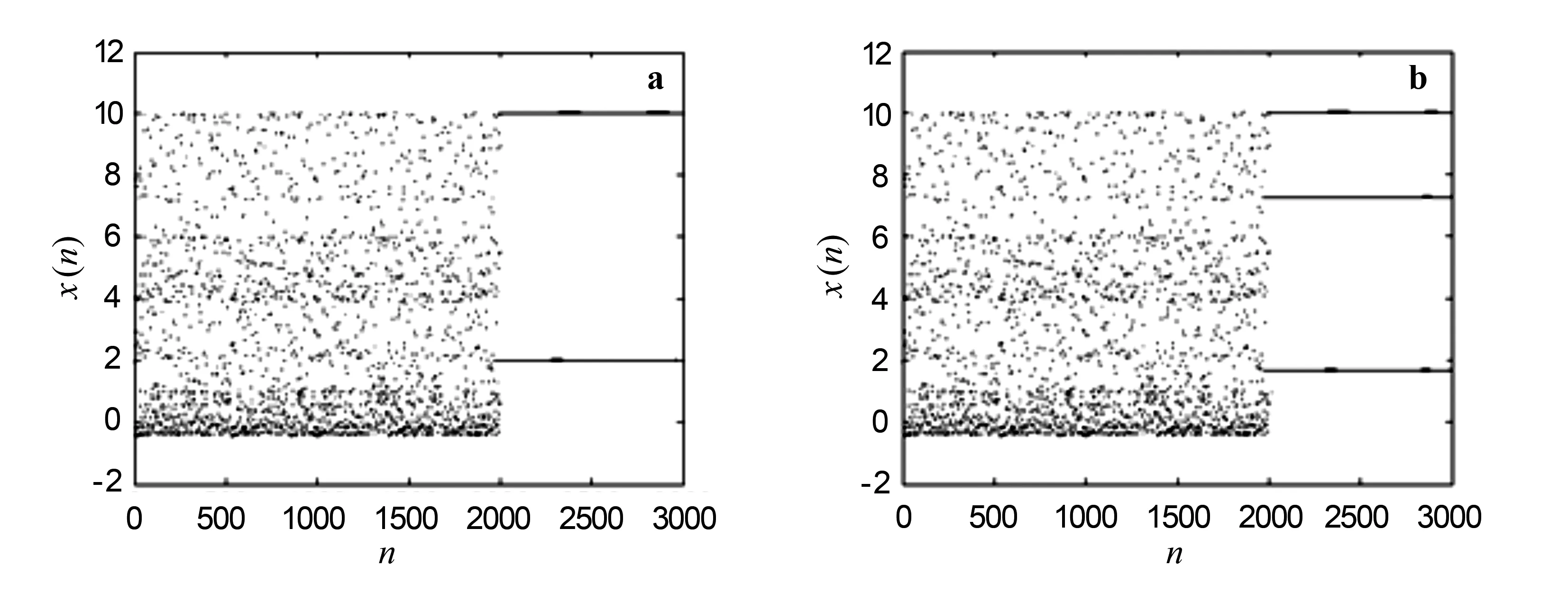
图5 二维离散混沌映射控制结果
4 结论
本文对含有理分式的一维离散映射的动力学行为进行了研究,运用全局分岔图和Lyapunov指数谱工具讨论了该离散映射的运动状态,并得到了该映射混沌态的形成过程.同时,在此基础上构造了二维含有理分式离散映射,运用最大Lyapunov指数谱和全局分岔图研究了该二维有理分式离散映射的非线性耦合参数对该映射的影响,结果显示该离散映射具有更加丰富的动力学行为,最后从理论和数值仿真两个方面实现了小波变换映射压缩法对该混沌映射的有效控制.
参考文献:
[1]Wu Z M,Xie J Y,Fang Y Y. Controlling chaos with periodic parametric perturbations in Lorenz system[J]. Chaos,Solitons and Fractals,2007,32:104-112.
[2]彭建华,刘秉正.非线性动力学[M].北京:高等教育出版社,2004:485-498.
[3]曹书豪,徐红梅.Logistic映射及其混沌序列特性分析[J].延边大学学报:自然科学版,2014,40(2):134-137.
[4]胡岗,萧井华,郑志刚.混沌控制[M].上海:上海科技教育出版社,2000:120-186.
[5]Yagasaki K. Extension of a chaos control method to unstable trajectories on infinite-or finite-time intervals: experimental verification[J]. Phys Lett A,2007,36(8):222-226.
[6]李险峰,张建刚,褚衍东,等.Lozi混沌映射的线性反馈控制[J].河北师范大学学报,2007,31(4):479-483.
[7]张永祥,俞建宁.Jeffcott碰摩转子系统混沌控制研究[J].山东大学学报:工学版,2006,10(5):117-119.
[8]Lu Jun'an,Wu Xiaoqun,Lü Jinhu,et al. A new discrete chaotic system with rational fractionation and its dynamical behaviors[J]. Chaos Solitons and Fractals,2004,22:311-319.
[9]彭战松,俞建宁,彭建奎.一个新离散系统的混沌控制与反控制[J].天津师范大学学报,2008,28(4):54-56.
[10]Shi Y,Chen G. Discrete chaos in Banach spaces[J]. Science in China Series A: Mathematics,2005,48(2):222-238.
