一类三对角矩阵特征对的分段快速算法
2014-07-31唐达
唐 达
(上海电机学院 数理教学部,上海201306)
在许多科学与工程计算中,常需要计算矩阵的特征值。而对于对称矩阵,一般是将其约化为三对角矩阵后再求其特征值;另外,三对角矩阵的特征问题也常作为原始问题出现。因此,三对角矩阵的特征问题长期来为许多学者所关注,如美籍华人数学家顾明关于三对角矩阵分-治算法的研究成果[1]在SIAM第六届应用线性代数会议上获最佳论文。
当今,计算三对角矩阵特征问题的方法很多,有QL或 QR 算法[2]372-373[3-4]、二(多)分法[2]391-397[5-9]、分-治算法[2]391-397[1,7,10-11]、同 伦 法[7,12]以 及 其 他 的一些迭代算法[7,13]。其中,二(多)分法、分-治算法、同伦法等都能用于并行计算。
一般来讲,计算一个n阶三对角矩阵的n个特征对,其计算量总不小于O(n2);而本文利用一类三对角矩阵特征对的局限性质,来计算大型非对称矩阵,其计算量仅为O(n)。本文的算法也非常适合并行计算,其并行效率较高。
1 三对角矩阵t向量的衰减性质
设A为n阶实三对角矩阵,t=(t1,t2,…为n维实向量。若

式(1)中右端向量仅第n个分量w不为零,则称t为A所对应的t向量[14-15]。可以证明,对角占优三对角矩阵(i=2,3,…,n)。也就是说,t向量之分量的绝对值是随i的减小而衰减的。实际上,除对角占优矩阵外,有很大一类三对角矩阵具有这种衰减性质。
考虑元素为正态分布N(0,1)上的随机三对角矩阵A,其t向量的平均增长率为
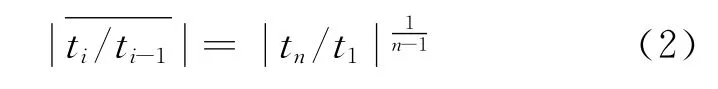
设n=120,进行104次的计算,即样本容量为104,由此绘出的的频率密度直方图[16]如图1所示。由 MATLAB函数 mean及var可算得此时样本的均值为1.69,方差为0平.0均3 11 6/1。.6由9此的可速知率,衰在减这。种情况下将以

图1 频率密度直方图Fig.1 Frequency histogram
若随机矩阵A的元素为(0,1)上均匀分布的随机数,则用与上述相同方法可算得的均值为1.40,方差为0.016 5,故此时t向量旳衰减率比上述要低。
以上所述,t向量是从矩阵A的左上方计算到右下方。若t向量是从矩阵A的右下方计算到左上方,即式(1)右端向量的第1个分量变为w、第n个分量变为零,由于A是随机矩阵,故此时的均值及方差均不变。
2 一类三对角矩阵特征对的局限性质
仍以元素服从N(0,1)分布的随机三对角矩阵A为例,设n=1 000。若任意截取A中一段n1=200阶的子矩阵A1,则称A为主矩阵、A1为子矩阵。图2所示为A1的2个特征向量之分量的绝对值或模(取对数值)随分量下标i变化的曲线。特征向量之分量的绝对值或模也同t向量一样具有相同的衰减率。因此,由图2可见,特征向量曲线在其最大值处向两旁逐渐减小。其中曲线1在子矩阵A1的两端已衰减,接近于零,故曲线1所对应的A1的特征对也可近似地看做主矩阵的特征对,这就是特征对的局限性质。此时,要计算主矩阵A的特征对,可以由计算子矩阵A1的特征对取得;由于截断,曲线2在子段的左端特征向量的分量并不趋于零,故该曲线对应的特征对不能看做主矩阵的特征对。由此可见,子矩阵A1的特征对只有一部分是属于主矩阵A的。数值实验表明,此时A1中约有82%的特征值是属于A的。子矩阵的阶数越大,百分比越大;反之,越小。
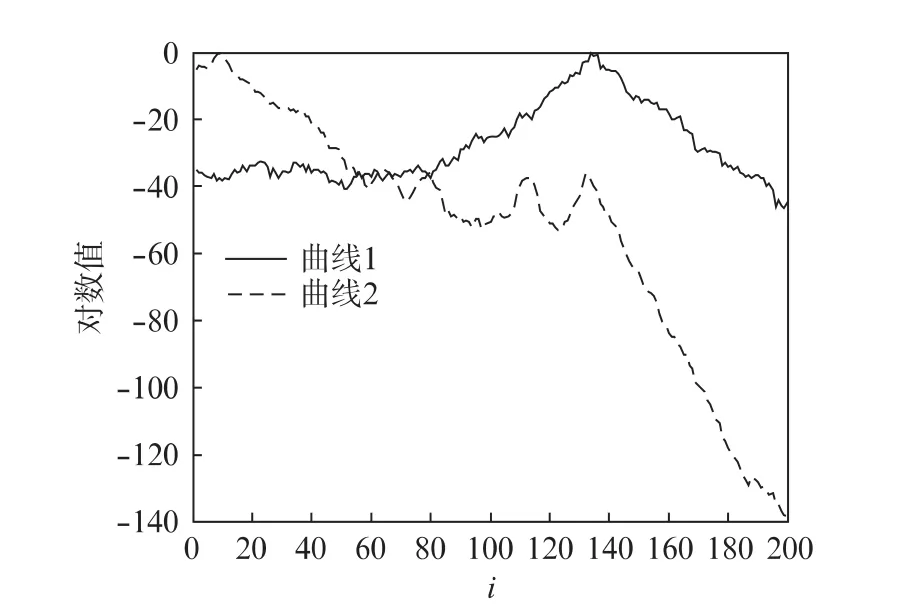
图2 特征向量曲线Fig.2 Curve of eigenvector
除上述呈正态分布的随机矩阵外,服从均匀分布、t分布等的随机三对角矩阵及Wilkinson测试矩阵等其特征对也都具局限性质。在特征对具局限性质的三对角矩阵中,随机矩阵占大多数,而当今随机矩阵无论在理论上还是实用上都具有一定的价值[17-18]。
3 分段算法
本文将特征对具有局限性质的主矩阵A分成互相有重叠的k段,以形成子矩阵A1,A2,…,Ak;再从这些子矩阵的特征对中分离出属于主矩阵A的特征对,由此求得A的全部特征对。
从子矩阵的特征对中分离出n个属于主矩阵的特征对,而其计算量又要小于O(n2),是一件较困难的事。所用的软件功能不同,分离的方法也不尽一样。本文采用Matlab软件进行分离。
在图2中,可以把特征向量之分量绝对值或模最大处的下标i形象地看成其对应的特征值的位置。因此,分离特征值就是把每个子矩阵(子段)两端的特征值剔除,留下中间属于主矩阵的特征值。
假定将主矩阵A分成A1、A2、A33段有互相重叠部分的子矩阵。每段长度(阶数)为1.5m,其中,m为分段长参数,重叠部分为0.5m。再将主矩阵分成有互相重叠部分的B1、B22段,每段长度(阶数)为2.5m。主矩阵的长度(阶数)为3.5m,如图3所示。m的值不能太小,否则,分离出的特征值误差太大。如对于服从N(0,1)分布的随机三对角矩阵,m不应小于120。

图3 矩阵分段Fig.3 Piecewise matrix
先求出子矩阵A1、A2、B1的全部特征值,然后找出B1的特征值与A1、A2中数值最接近的2.5m个特征值,令这些特征值的集合为Ω1。Ω1中属于A1的特征值也应属于主矩阵A,记此集合为Λ1,则Ω1中属于A2的特征值的集合Λ2=Ω1-Λ1。再求出子矩阵A2、A3与B2的全部特征值,找出B2的特征值与A2、A3中数值最接近的2.5m个特征值,记此集合为Ω2。Ω2中属于A3的特征值也应属于主矩阵A,记此集合为Λ4。Ω2中属于A2的特征值的集合Λ3=Ω2-Λ4。再求Λ2与Λ3的交集Ψ1=Λ2∩Λ3。Ψ1中的特征值也应属于主矩阵A。因此,集合Ψ=Λ1+Ψ1+Λ4中的特征值就是主矩阵A中的3.5m个特征值。
Ψ中的特征值所对应的子矩阵的特征向量并不能作为主矩阵A的特征向量,因为特征向量衰减得较慢,若以此作为主矩阵的特征向量将带来较大误差。解决的办法是将每段1.5m的长度再向两端延长一些,在延长的子矩阵中求特征向量,这就可以近似地看作主矩阵的特征向量。
4 分段算法程序
假定将主矩阵A分段成k个子矩阵A1,A2,…,Ak,则有如上文所述特征值的计算层次,如图4所示。
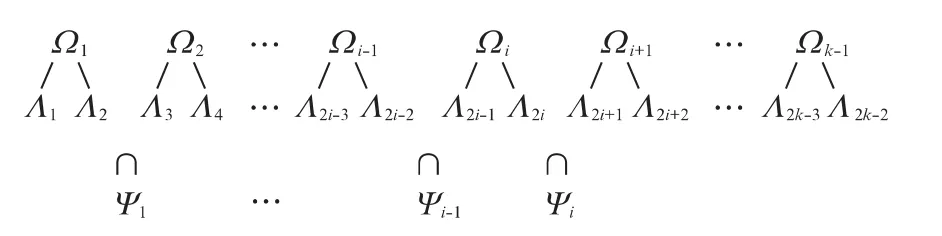
图4 计算层次Fig.4 Computational hierarchy
先计算Ωi,将Ωi中属于2个子矩阵的特征值分成Λ2i-1、Λ2i2个集合,求Λ2i、Λ2i+1的交集
Ψi=Λ2i∩Λ2i+1,i=1,2,…,k-2
最后,集合

中的特征值就是主矩阵A的全部特征值。
算法程序是用MATLAB语言编写的,其中相关的函数参见文献[19] 。程序步骤如下:
(1)输入矩阵A、分段长参数m、分段数k、矩阵A的阶数n=(k+0.5)m以及为了精确计算特征向量而将子段端部延长的数值Δm;
(2)将A以1.5m的长度(阶数)分段成A1、A2、…、Akk个子矩阵,再以2.5m的长度分段成B1、B2、…、Bk-1k-1个子矩阵,各矩阵间的相互位置如图3所示;
(3)计算A1、A2及B1的特征值,利用dsearchn函数求出集合Ω1,利用find函数求出Λ1及Λ2;
(4)将子矩阵A1的右端延长Δm,以集合Λ1中的特征值用逆迭代法求其特征向量;
(5)Fori=2∶k-1;
(6)计算Ai、Ai+1、Bi的特征值,求出集合Ωi、Λ2i-1及Λ2i;
(7)利用intersect函数求出Λ2i-2、Λ2i-1的交集Ψi-1;
(8)将子矩阵Ai的两端延长Δm,以集合Ψi-1中的特征值用逆迭代法求其特征向量;
(9)end
(10)计算集合Λ2k-2;
(11)将子矩阵Ak的左端延长Δm,以集合Λ2k-2中的特征值用逆迭代法求其特征向量;
(12)输出用式(3)计算得到主矩阵A的n个特征值,以上算得的特征向量即为A的全部特征向量。
5 数值算例
本文算例使用的PC机CPU为AMD 2.59GB,内存2GB。用Matlab 7.12.0语言编程计算,共计算3例。
例1 元素服从N(0,1)分布的随机三对角矩阵,为非对称矩阵,其特征对可能是复数。其中,m=120,Δm=0.45m。
例2 元素服从N(0,1)中均匀分布的随机三对角矩阵,为对称矩阵。其中,m=160,Δm=0.45m。
例3 Wilkinson测试矩阵,其非对角元素均为1,对角元素依次为n/2+1-i(i=1,2,…,n)。其中,m=100,Δm=0.45m。
计算结果列于表1中。每个子矩阵的特征值用Matlab eig函数计算,而特征向量则用逆迭代法计算得到。例1与例2每例均重复计算10次,计算时间为10次的平均值;例3只计算1次。表中,ε为本文算法分段算得的特征值与Matlab eig函数算得的特征值之差的绝对值或模;e为本文算法算得的特征向量与Matlab eig函数算得的特征向量其对应的各分量之差的绝对值或模的最大值。
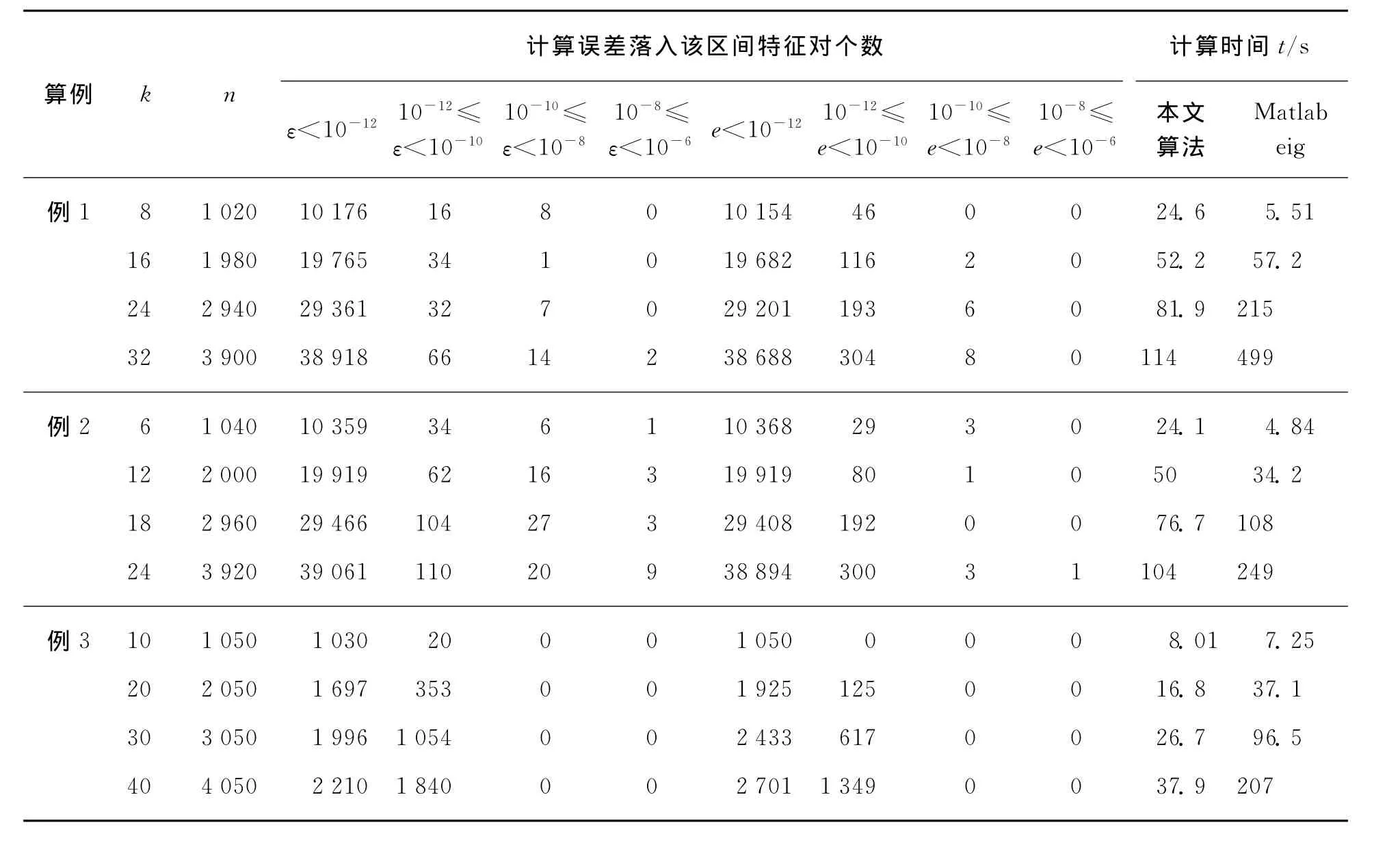
表1 算例的计算精度及计算时间Tab.1 Computation precision and consumed time for the examples
由表可见,计算精度是满意的,而计算时间仅供参考。由于同一个问题用Matlab内部函数计算要比用Matlab语言编程计算的速度约快300%~1 000%。但从表中可见,本文算法的计算用时与矩阵阶数n大致呈线性关系,而Matlab是用满矩阵求特征对的,故计算用时约与n3成比例。一般来讲,用QR迭代法或二分法计算三对角矩阵的特征值,其计算量为O(n2)。
6 结 语
本文所述分段快速算法适合于大型非对称三对角矩阵,对n个特征对的计算复杂性仅为O(n),这是目前文献中不曾见的,只要矩阵的特征向量具局限性质,就能采用本文算法。从理论分析及算例均可见,计算具有较高精度。本文算法也非常适合并行计算。
[1] Gu Ming,Eisenstat S C.A divide-and-conquer algorithm for the symmetric tridiagonal eigenproblem[J] .SIAM Journal on Matrix Analysis and Application,1995,16(1):172-191.
[2] Golub G H,Van Loan C F.矩阵计算[M] .袁亚湘译.3版.北京:人民邮电出版社,2011:372-373,391-397.
[3] 何光渝,高永利.Visual Fortran常用数值算法集[M] .北京:科学出版社,2002:357-363.
[4] 何渝.计算机常用数值算法与程序[M] .北京:人民邮电出版社,2003:137-140.
[5] Wilkinson J H.代数特征值问题[M] .石钟慈,邓健新,译.北京:科学出版社,2001:310-318.
[6] 曹志浩,张玉德,李瑞遐.矩阵计算和方程求根[M] .2版.北京:高等教育出版社,1984:159-177.
[7] 邓健新.解实对称矩阵特征值问题的并行算法[J] .数值计算与计算机应用,1997,18(4):246-258.
[8] 刘艳红,吕全义.Jacobi矩阵特征值的并行算法[J] .纺织高校基础科学学报,2011,24(1):21-25.
[9] Roopamala T D,Katti S K.Eigenvalue of tridiagonal matrix using Strum sequence and Gerschgorin theorem[J] .International Journal on Computer Science and Engineering,2011,3(12):3722-3727.
[10] 罗晓广,李晓梅.求解对称三对角矩阵特征值的一种新的分而治之算法[J] .数值计算与计算机应用,1997,18(1):74-80.
[11] Coakley Ed S,Rokhlin V.A fast divide-and-conquer algorithm for computing the spectra of real symmetric tridiagonal matrices[J] .Applied and Computational Harmonic Analysis,2013,34(3):379-414.
[12] Brockman P,Carson T,Cheng Yun,et al.Homotopy method for the eigenvalues of symmetric tridiagonal matrices[J] .Journal of Computational and Applied Mathematics,2013,237(1):644-653.
[13] Matsekh A M.The Godunov-inverse iteration:A fast and accurate solution to the symmetric tridiagonal eigenvalue problem[J] .Applied Numerical Mathematics,2005,54(2):208-221.
[14] 唐达.三对角矩阵计算[J] .高等学校计算数学学报,1997,19(2):97-104.
[15] 唐达.周期三对角矩阵求逆的快速算法[J] .上海电机学院学报,2013,16(5):300-304.
[16] 何正风.MATLAB概率与数理统计分析[M] .2版.北京:机械工业出版社,2012:87.
[17] 曾杏元.有关随机矩阵领域最新研究动态与进展的综述报告[J] .数学理论与应用,2011,31(3):7-19.
[18] 王磊,郑宝玉,崔景伍.随机矩阵理论与无线通讯[J] .南京邮电大学学报:自然科学版,2010,30(3):90-96.
[19] 徐东艳,孟晓刚.MATLAB函数库查询辞典[M] .北京:中国铁道出版社,2006:161,216,321.
