基于统计聚类与时序分析的风电场短期风速预测模型
2014-09-14陈勤勤陈国初
陈勤勤, 陈国初
(上海电机学院 电气学院, 上海 200240)
基于统计聚类与时序分析的风电场短期风速预测模型
陈勤勤, 陈国初
(上海电机学院 电气学院, 上海 200240)
在时间序列预测法的基础上,运用统计聚类分析的方法对历史风速数据进行预处理,综合考虑了气象因素对风速的影响。根据预测日的平均风速、最大和最小风速、风向及温度等特征参数,按照相似性最大的原则,选择合适的风速数据作为预测建模用的训练样本。与未经预处理的数据所建立的模型相比,预测精度得到了显著提高,并验证了采用统计聚类分析来预处理数据的正确性,为更精确地预测风电功率提供了条件。
风速预测; 时间序列分析; 统计聚类分析; 相似性原则; 预测精度
目前,全球能源危机日益加剧,而常规能源难解燃眉之急,故人们对可再生能源开发、利用的研究越来越重视。风能作为一种新的自然能源,具有蕴量巨大、可再生性和无污染等优点,故风力发电日益受到世界各国的重视。风电场输出的发电功率与其风速有很大关系,具有很强的波动性和随机性。随着我国风力发电机组装机容量的增加,风电接入电网后对电网的稳定性和频率影响不断增大,故准确预测风电场风速,对于电力部门及时调整调度计划、衡量风电场容量的可信度,进而确定合适的风电上网价格,具有重要的现实意义。同时,准确预测风电场的风速及功率,也是缓解电力系统调峰、调频压力,提高风电接纳能力的有效方法之一[1-2]。
目前,风电场风速预测多采用组合预测模型,依赖于单一预测模型的精度和组合的算法,预测精度较高,故单一预测方法依然是风速预测研究的基础和重点。风速预测的单一方法有很多,包括时间序列法[3-4]、卡尔曼滤波法(Kalman-filter)[5-6]、人工神经网络法(Artificial Neural Network, ANN)[7]、小波分析法(Wavelet Analysis)[8-9]、模糊逻辑法(Fuzzy Logic)[10]、支持向量机(Support Vector Machine, SVM)[11],它们预测的相对误差为25%~40%[12]。由于时间序列预测法仅需要风电场单一的风速数据就可以对不平稳的时间序列进行建模,故该方法简单易行,且预测效果显著,在风电场风速和发电功率的预测中应用广泛。
利用时间序列预测法预测风速需要总结与归纳大量的历史数据得出反映其变化规律的数学表达式,进而建立起预测模型来进行预测,故输入的历史数据对预测模型的建立及参数的选取有很大的影响。因此,合理地选择输入样本,可以有效地提高预测模型的精度。
基于上述分析,本文运用统计聚类分析方法,对历史日的风速数据进行分类筛选;利用预测日已有的风速特征数据以及数值天气数据,按照相似性最大的原则,选择与预测日相似性最大的那组数据作为预测建模的训练样本,进而对待测日风速进行预测;并将预测结果与未运用聚类分析筛选的数据、未考虑数值天气因素的预测结果进行比较,最终给出最合适的风速预测方案。
1 风速预测模型
1.1风速数据的聚类分析
统计聚类是聚类分析中较为常用的一种方法。它主要依据样本之间不同程度的相似性将样本划分为不同的类别,其中将相似程度较大的样本聚为一类。
距离判据和相似系数是衡量相似性程度的两种主要方法[11]。对于数值型数据通常使用距离判据,距离越接近零,则相似性越大。
假设每个样本有m个指标特征,则欧式距离可定义为[13]
(1)
式中,xjl和xil分别为第j、i个样本的第l个指标值。
本文将统计聚类分析与时间序列法相结合,通过统计聚类分析对原数据进行筛选,选出与待测日的风速特征因素相类似的历史日的风速数据,将它们作为预测建模用的样本,利用气象部门提供的预测日的平均风速、最大和最小风速、风向以及温度的信息作为预测日的特征参数,利用距离判据(欧氏距离)作为相似性度量来预测风速。
1.2时间序列法建模
时间序列模型可分为自回归(Auto Regressive, AR)模型、滑动平均(Moving Average, MA)模型、自回归滑动平均模型(Auto Regressive Moving Average, ARMA)和累积式自回归滑动平均(Auto-Regressive Intergrated Moving Aver-eage, ARIMA)模型等。其中,AR模型描述的是系统对过去自身状态的记忆;MA模型描述的是系统对过去时刻进入系统的噪声的记忆;而ARMA模型则是系统对过去自身状态以及各时刻进入的噪声的记忆,是AR和MA模型的结合。ARIMA模型主要用来描述非平稳时间序列。而ARMA、AR、MA模型主要用来描述平稳时间序列。对于非平稳ARIMA模型可以通过差分后转化为平稳模型来处理。
由于风速数据是非平稳时间序列,故本文先建立ARIMA模型,然后对其进行平稳化处理后,转化为AR、MR、ARMR模型来处理。
1.2.1 模型描述 时间序列模型简称B-J法[14]。设{y1,y2,…,yt,…}是零均值平稳序列,满足
yt-φ1yt-1-…-φpyt-p=
εt-θ1εt-1-…-θqεt-q
(2)
式中,t为时间;φ1,φ2,…,φp和θ1,θ2,…,θq均为常数;干扰项{εt}为零均值、方差为σ2ε的平稳白噪声序列;{yt}为阶数为p、q的自回归滑动平均序列,记为ARMA(p,q)序列;当q=0时,yt为 AR(p) 序列;当p=0时,yt为MA(q)序列。
令Bmyt=yt-k,Bmεt=εt-m,则式(2)可化为
φ(B)yt=θ(B)εt
(3)
式中,
φ(B)=1-φ1B-φ2B2-…-φpBp
θ(B)=1-θ1B-θ2B2-…-θqBq
B为滞后算子。
对于非平稳时间序列,必须先对其进行平稳化处理,才能运用上述3种模型描述,方法如下:
(1) 有序差分变换。若所研究的时间序列具有随机性,可对其进行有序差分变换。假设用=1-B来表示差分算子,n阶差分后有

(4)
若序列已平稳,则原时间序列为

(5)
即为累积式自回归滑动平均模型ARIMA(p,q)。
(2) 季节性差分变换。若所研究的时间序列具有季节性变化趋势,可对其施行季节性差分变换。引入季节性差分算子s=1-Bs,则季节性ARIMA模型为

(6)
式中,Φ(B)=1-Φ1Bs-Φ2B2s-…-ΦPBPs为季节自回归算子;其中,P为季节自回归阶数,Θ(B)=1-Θ1Bs-Θ2B2s-…-ΘQBQ s为季节移动平均算子,Q为季节移动平均阶数;D为季节差分阶数;s为 季节周期,当时间序列为月度数据时,s=12;当时间序列为季度数据时,s=4。
1.2.2 模型建立 本文采用的Akaike信息准则(Akaike Information Criterion, AIC)由日本统计学家Akaike于1973年提出[15-16]。时间序列ARMA(p,q)中,AIC定阶准则是通过适当地选择p与q,使得
(7)
式中,N为样本容量;方差估计值与p、q有关。当p=,q=时,其中,、为p、q的估计值,则式(7)达到最小值,认为序列ARMA(p,q)为ARMA(,)。
确定模型阶数后,采用最大似然法估计模型中的参数,并进行χ2检验,模型的残差为
εt=Yt-Y-
2 实例研究
2.1样本的选取
实例数据来源于2007年6月(30天)东北某风电场40#机组,每小时记录一组数据,其中包括功率、70m处风速、风向和温度,共720组。本文以预测6月23日的风速为例,样本的选取方式有3种: ① 按距离待预测日最近的前7天的数据作为预测样本;② 仅考虑平均风速,选出与待预测日风速平均值欧式距离最短的7组数据作为预测样本;③ 考虑了风速、风向、温度,经过一系列加权平均,选出与待预测日欧式距离最短的7组数据作为预测样本,即通过统计聚类分析对历史数据进行处理。然后,分别应用时间序列法建模,预测风速,并对得出的预测结果进行比较,选出比较好的预测方法。本文主要介绍第3种方法的样本选取。
2.2数据处理与分析
选取日平均风速、最大风速、最小风速、平均风向、最大风向、最小风向、平均温度、最大温度、最小温度数据作为待预测日的风速特征参数,计算出各历史日与待预测日的风速属性值之间的欧氏距离,然后对数据进行加权平均,选出其中相似性最高(最终加权得到的最短欧式距离)的7个历史日的数据作为预测样本。
(1) 以风速为例,按式(1)计算出各历史日与待预测日之间风速的平均、最大、最小值的欧式距离,并分别用xS、yS、zS表示。同理,计算出各历史日与待预测日之间风向、温度的平均、最大、最小值的欧氏距离,并分别用(xD、yD、zD)、(xT、yT、zT)表示。
(2) 对上述计算出的风速的平均、最大、最小欧式距离进行加权平均,得
(8)
式中,w1、w2、w3分别为各项所占的权重。本文中分别取0.6、0.2、0.2。
同理,将计算出的风向、温度的平均、最大、最小欧式距离进行加权平均,分别用dD、dT表示。
(3) 对dS、dD、dT再进行加权平均,得
(9)
式中,θS、θD、θT为风速、风向、温度所占的权重,考虑到风速是影响风电功率的直接因素,本文中分别取0.7、0.2、0.1。
将上述数据处理过程中选出与等测日相似性最高的7个历史日风速数据(共168个)作为预测样本。建模前,对风速数据序列的平稳性进行检验,计算风速样本值的前20个自相关函数值ρk和偏相关函数值αkk其中,k为数据个数。图1为待预测日前7天(168个)原始风速数据时间序列{Yt},表1为风速数据的自相关与偏相关函数值,图2为{Yt}的自相关函数图。
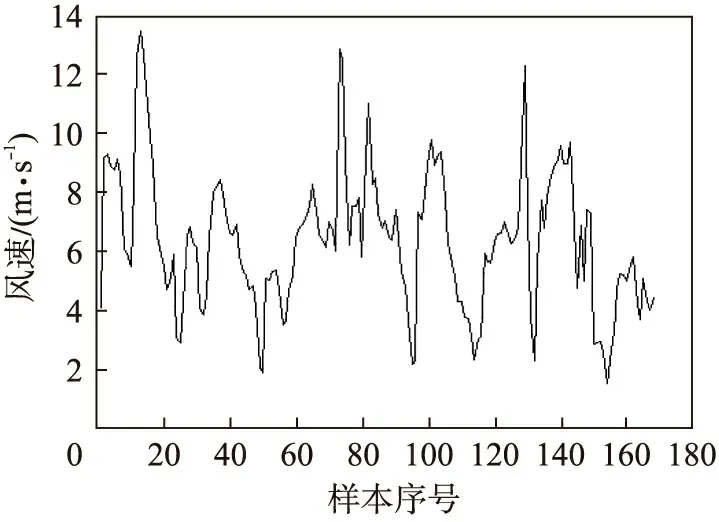
图1 原始风速时间序列图Fig.1 Original wind speed time series
由表1、图2可知,风速数据的自相关系数不能很快地衰减至零,故该时间序列是非平稳的,需要对该风速序列进行平稳化和零均值化处理。

表1 风速数据的自相关与偏相关函数值Tab. 1 Autocorrelation and partial autocorrelation of wind speed data

图2 风速序列差分前的自相关函数值ρk变化趋势Fig.2 Autocorrelation of wind speed sample sequence before difference calculation
通过一阶差分,将非平稳序列转化为平稳序列,图3为对原时间序列进行一阶差分后得到的序列{Y′t},其对应的相关计算结果如表2所示。
由图3和表2看出,序列的自相关系数能较快地落入随机区域内,由此初步判断该序列是平稳的。
2.3模型建立
由表2可知,自相关函数具有“截尾”性,偏相关函数具有“拖尾”性,故可对差分后的时间序列建立ARMA(p,q)模型,再由AIC定阶准则确定p、q的值。经Matlab编程计算,当p=1,q=2时,AIC的值最小,故模型为ARMA(1,2)。

图3 风速序列经一阶差分后的自相关函数值ρk变化趋势图Fig.3 Autocorrelation of wind speed sample sequence after first-order difference
表2经一阶差分后的自相关与偏相关函数值
Tab. 2 Autocorrelation and partial autocorrelation of wind speed data after first-order difference
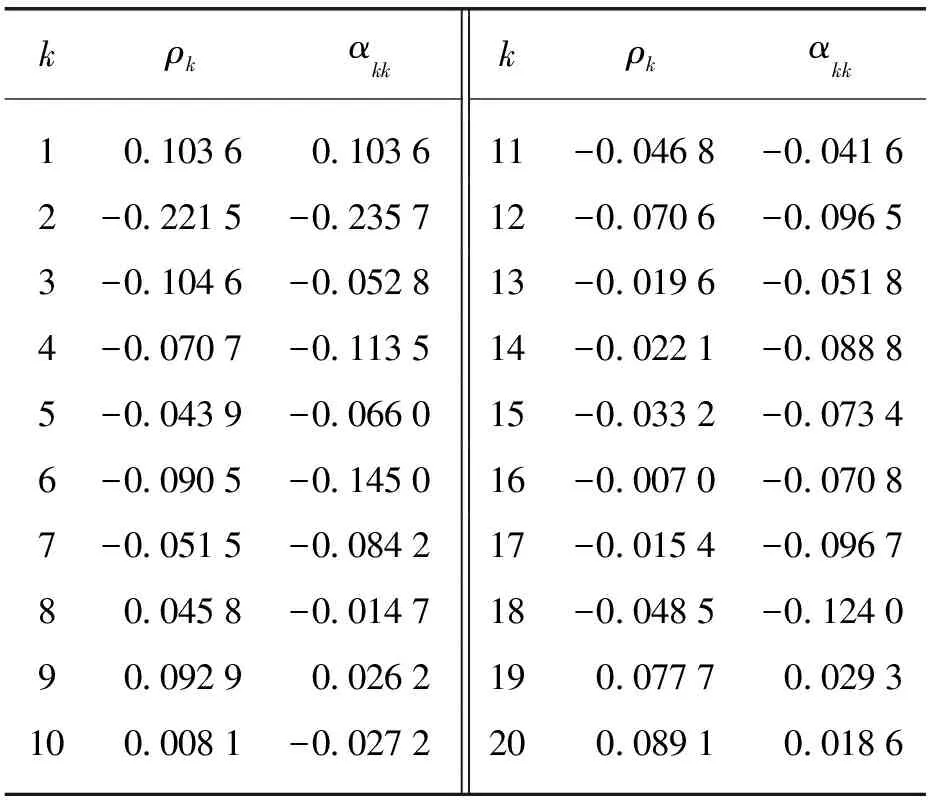
kρkαkkkρkαkk10 10360 103611-0 0468-0 04162-0 2215-0 235712-0 0706-0 09653-0 1046-0 052813-0 0196-0 05184-0 0707-0 113514-0 0221-0 08885-0 0439-0 066015-0 0332-0 07346-0 0905-0 145016-0 0070-0 07087-0 0515-0 084217-0 0154-0 096780 0458-0 014718-0 0485-0 124090 09290 0262190 07770 0293100 0081-0 0272200 08910 0186
模型确定后,用最大似然估计法对其参数进行估计,从而得到残差序列为
εt=
yt-0.056yt-1+0.076εt-1+0.072εt-2
(10)
经检验可知,{εt}为白噪声序列,则模型通过检验,可以用来预测。
2.4衡量预测结果
使用相对误差[18]来衡量预测结果。相对误差为
(11)
式中,x*为预测值;x为真实值。
3 预测结果与分析
本文利用3种方法选取样本,分别建立时间序列模型,并对风速进行预测。表3给出了利用 3种 方法选取样本进行预测,得到的6月23日 0:00~ 23:00的风速预测结果对比。由表3可知,利用3种方法获取样本进行预测,得到的预测值;误差逐步减小。这是由于获取样本时,方法1仅利用按时间顺序排列的历史数据作为预测样本,没有对样本进行选择,故其精确度较差;方法2考虑了相似性,即考虑了与待预测日平均风速最接近的几组数据作为样本,对历史数据进行了选择;方法3不仅考虑了平均风速,还考虑了温度、风向对风速的影响,即在前两种方法的基础上考虑了数值天气的影响。由于风向、温度对风电功率的影响程度较小,故方法3与方法2的平均相对误差很接近。为进一步检验方法3的可靠性、有效性,对其他多处历史时间的风速值分别进行反复建模预测分析。本文给出了使用本文方法预测6月19日和6月30日的风速预测结果,如表4所示。
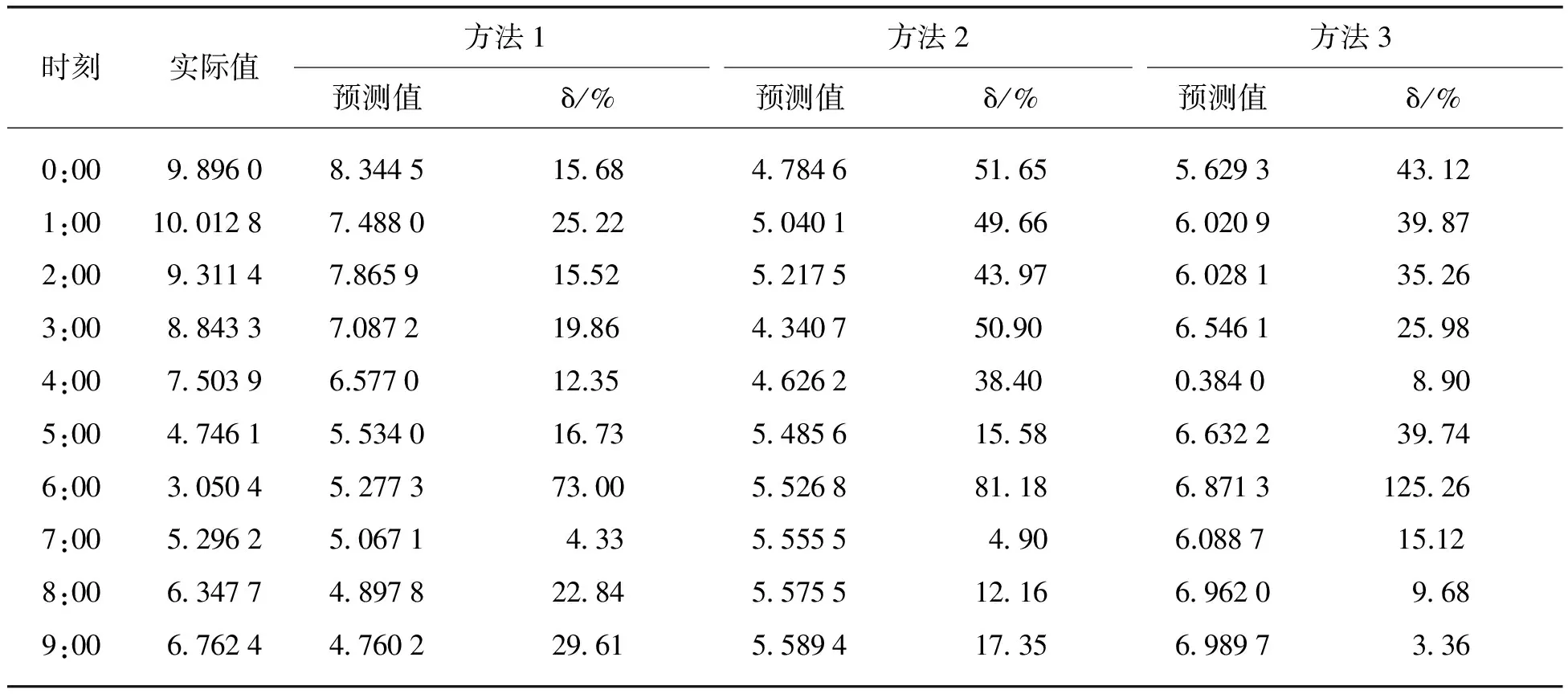
表3 利用3种方法获取样本的对比预测结果Tab. 3 Comparison of predicted wind speed in three different ways

(续表3)
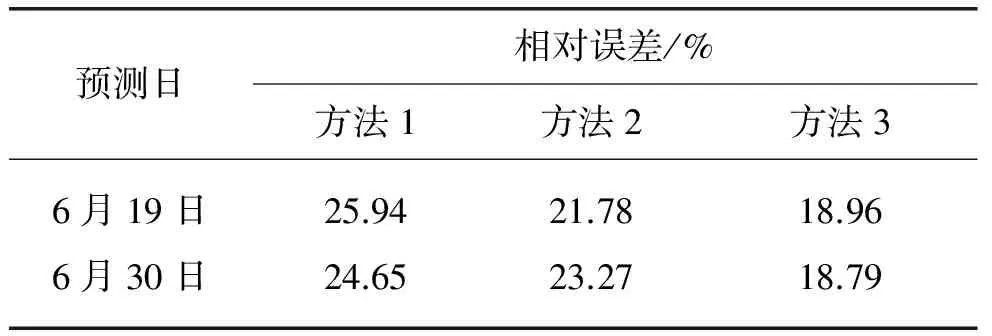
表4 6月19、30日的风速预测结果Tab. 4 Wind speed forecasting results of June 19 and June 30
由表4可见,3种预测模型的日平均误差逐渐减小,其中第3种方法由于考虑了风速、风向、温度等的影响,运用聚类分析处理数据,选出合适的样本,最后在一定程度上提高了预测精度,从而实现了预期的目标。
4 结 语
风电场风速预测问题是一个非常复杂的问题。鉴于风电场风速的变化受到诸多因素的影响,本文提出了将统计聚类分析应用于时间序列法来预测风速。通过对气象部门提供的预测日风速、风向、温度的特征作为聚类分析指标,采用欧式距离作为确定相似日的依据,挑选出新的训练样本,运用ARMA模型进行预测,在一定程度上提高了预测精度。虽然通过对几组数据的预测结果进行分析,利用本文方法进行风速预测的误差还是偏大,尤其是对变化比较剧烈的风速进行预测时误差较大,这可能与运用聚类分析时选用的权值大小有关,今后将对权值的选取等问题作进一步研究。
[1] 范高锋,裴哲义,辛耀中.风电功率预测的发展现状与展望[J].中国电力,2011,44(6): 38-41.
[2] 高阳,陈华宇,欧阳群.风电场发电量预测技术研究综述[J].电网与清洁能源,2010,26(4): 60-63,67.
[3] 李东福,董雷,礼晓飞,等.基于多尺度小波分解和时间序列法的风电场风速预测[J].华北电力大学学报,2012,39(2): 43-48.
[4] 王国峰,王子良,王太勇,等.Matlab在时间序列分析中的应用[J].应用科技,2003,30(5): 36-38.
[5] Louka P, Galanis G, Siebert N, et al. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J]. Journal of Wind Engineering and Industrial Aerodynamics,2008,96(12): 2348-2362.
[6] Che Guan,Luh P B,Wen Cao.Short-term wind generation forecasting and confidence interval estimation based on neural networks trained by extended Kalman particle filter[C]∥2011 9th World Congress on Intelligent Control and Automa-tion(WCICA).Taipei: IEEE,2011: 1173-1179.
[7] Suarez R R,Graff M.Modeling ANNS performance on time series forecasting [C]∥2013 IEEE International Autumn Meeting on Power,Electronics and Computing.Mexico City: IEEE,2013: 1-6.
[8] 王鹏,陈国初,徐余法,俞金寿.改进的EMD及其在风电功率预测中的应用[J].控制工程,2011,18(4): 588-591,599.
[9] 刘辉,田红旗,李燕飞.基于小波分析法与滚动式时间序列法的风电场风速短期预测优化算法[J].中南大学学报: 自然科学版,2010,41(1): 370-375.
[10] 李伯颐.基于模糊聚类处理的风电场短期风速和发电功率预测[D].上海: 上海交通大学,2009: 12-44.
[11] 张广明,袁宇浩,龚松建.基于改进最小二乘支持向量机方法的短期风速预测[J].上海交通大学学报,2011,45(8): 1125-1129,1135.
[12] 方江晓,周晖,黄梅,等. 基于统计聚类分析的短期风电功率预测[J].电力系统保护与控制,2011,39(11): 67-73,78.
[13] 杨纶标,高英仪,凌卫新.模糊数学原理及应用[M].广州: 华南理工大学出版社,2011: 87-91
[14] 易丹辉.时间序列分析方法与应用[M].北京: 中国人民大学出版社,2011: 63-88.
[15] 张文泉,李泓泽.极大似然估计与AIC准则联合建模[J].现代电力,1999,16(2): 78-82.
[16] 陈兴钩.统计模型用AIC准则定阶的相容性问题[J].华侨大学学报: 自然科学版,1989,10(1): 6-10.
[17] 彭晖.风电场风电量短期预测技术研究[D].南京: 东南大学,2009: 23-38.
[18] 李庆扬,王能超,易大义.数值分析[M].5版.北京: 清华大学出版社,2010.9: 4-5.
Short-Term Wind Speed Prediction Model Based onStatistical Clustering and Time Series Analysis
CHENQinqin,CHENGuochu
(School of Electric Engineering, Shanghai Dianji University, Shanghai 200240, China)
This paper is based on auto-regressive integrated moving-average (ARIMA) and uses statistical cluster analysis to preprocess the history wind speed data. Influence of meteorological factors on the wind speed is considered according to average, minimum and maximum wind speeds, wind direction, temperature and other parameters on the prediction day. Appropriate wind speed data are selected using the principle of maximum similarity as training samples for the prediction model. As a result, the prediction accuracy is significantly improved compared with the model without preprocessed data. Validity of using statistical cluster analysis to preprocess the history wind speed data is shown. The paper also gives conditions for more accurate wind power prediction.
wind speed prediction; time series analysis; statistical cluster analysis; principle of similarity; forecast precision
2013 - 10 - 25
上海市自然科学基金项目资助(11ZR1413900);上海市教育委员科研创新项目资助(13YZ140);上海市教育委员会重点学科资助(J51901)
陈勤勤(1988-),女,硕士生,主要研究方向为风电场输出功率预测及不确定性分析, E-mail: 97529944@qq.com
2095 - 0020(2014)02 -0076 - 07
TM 614
A
