水下圆锥双壳结构振声分析及减振优化
2014-07-31徐志亮翁章卓
徐志亮,翁章卓
(中国舰船研究设计中心,湖北 武汉 430064)
水下圆锥双壳结构振声分析及减振优化
徐志亮,翁章卓
(中国舰船研究设计中心,湖北 武汉 430064)
联合使用虚拟质量法和一般流固耦合有限元方法,分析某水下圆锥双壳结构在螺旋桨纵向激励下的振动情况,并用边界元方法进行声学计算。这种分析方法既能有效地计入内外流场对结构振动的影响,又避免了复杂的外场流体建模工作。此外,通过计算验证了液压动力减振器对降低螺旋桨纵振引发的辐射噪声具有良好效果。在理论方案的基础上提出一个简单可行的减振器参数优化方案,经过优化,进一步降低结构的辐射噪声。
流固耦合;虚拟质量法;辐射声功率;液压动力减振器
0 引 言
低频时,船体结构的振动声辐射预报常用有限元和边界元结合的方法来实现。商德江、何祚鏞[1]较早使用Ansys和边界元软件Sysnoise分析了水下双层加肋圆柱壳的模态和声辐射;姚熊亮[2]用同样的方法对一个单层加筋圆柱壳的水下振动声辐射特性进行分析,并结合实验验证该方法的有效性;徐张明[3]对某双壳潜艇整体建立了声固耦合有限元模型,再在边界元软件中进行声学预报;刘晓明[4]用有限元方法考虑内场流体耦合的作用分析了某船的舱内中低频噪声。然而,不论是水上水下,对象是简单的柱壳还是复杂的舰艇,综合考虑内外场流体耦合作用的振动声辐射研究却不多见。
本文研究螺旋桨纵向激励下一个水下圆锥加肋双壳结构的声辐射情况,全面考虑了内外场流体对结构振动的影响。水下振动问题的一个难点在于有限元模型的建立,通常要建立一个包络结构的球域流场,且要求流体与结构单元节点在流固交界面上重合,流域外表面要用吸声单元模拟无限远处的声学边界条件。此外,由于流场巨大,当激励频率较高时计算规模将非常大。本文用虚拟质量法来模拟外场耦合效应,对壳间流体则通过建立流体网格单元来处理。虚拟质量法通过提取结构的附加质量矩阵来模拟声振耦合作用,既可得到良好的模拟效果,又避免了繁琐的建模工作。
螺旋桨纵向激励是船舶振动的一个主要激励源,如何降低轴系纵振引发的辐射噪声一直是各方非常关注的一个课题。
Goodwin[5]提出一种液压动力减振装置,其分析表明该装置能有效吸收轴系纵向振动。本文先通过对比计算,验证这种装置良好的减振降噪效果。随后提出一种简便优化方案,对该装置的几个虚拟参数进行优化,得到了比理论方案更好的减振降噪效果。
1 振动方程
本文全面考虑结构内外场流体的耦合作用,外场耦合用虚拟质量法提取附加质量矩阵来进行模拟;内场耦合则通过建立流固耦合有限元模型来实现。
1.1 虚拟质量法
虚拟质量法假设流体不可压缩、无黏性、低流速。通过在流固边界上布置一系列源点,用Helmholtz方法求解Laplace方程,每一个源点对微分方程产生一个简单解。假设结构已知的运动和由源点激发的运动相同,导出一个线性矩阵方程,求解该方程得到源点强度。由源点值确定作用在结构上的有效压力,进而确定作用在各节点上的力,再由节点力得到结构振动的附加质量矩阵。
设σj是位置rj处流体源点的值,单位是单位面积的体积流量,假设它的作用范围是Aj,ui是其他任一位置ri处的速度矢量,则:
(1)
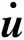
任意点i处的压力Pi为:
(2)
对式(1)和式(2)在单元表面积分结果以矩阵的形式给出:

(3)

(4)
式中{F}为节点力。设[Mf]为虚拟质量矩阵,{F}可以表示成:

(5)
由式(3)和式(4)可得:
[Mf]=[Λ][χ]-1。
(6)
1.2 流固耦合有限元方程
常规的流固耦合有限元矩阵方程可以写作:

(7)

2 求解声辐射的边界元方程
研究表明,边界元法是研究结构声辐射的一种常用方法,用边界元法预报结构低频噪声能获得较好精度。用直接边界元法处理外场声辐射问题需要求解以下方程:
[A(ω)]{p}=[B(ω)]{vn}。
(8)
式中:A(ω)和B(ω)为相关的边界元矩阵,都是非对称的稠密矩阵,且随频率变化;{p}和{vn}分别为耦合面上的压力和法向速度矢量。将有限元计算得到的{vn}代入式(8)得到交界面处的声压{p}。由{p}和{vn}可以求出空间任一场点处的声压、速度和加速度等量。任一场点处的声压可由下式求得:
Pp={a}t{p}+{b}t{vn}。
(9)
式(10)和式(11)分别定义了结构的入射声功率和辐射声功率:
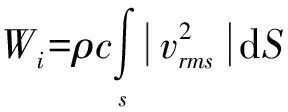
(10)

(11)
式中:ρ和c分别为介质密度和介质中声速;vrms为激励速度均方根;v*为边界外法线方向速度的共轭。
3 液压动力减振器
在螺旋桨对船体脉动激励中纵向激励占了主要成分,如何减小螺旋桨纵向激励诱发的船体振动及声辐射一直是一个备受关注的课题。Goodwin[5]在已有的动力减振装置的基础上设计了一种新型的液压动力减振器,该装置的结构如图1所示。

图1 液压动力减振器Fig.1 Hydraulic pressure dynamic vibration absorber
装置由1个截面积为A0的圆柱油缸,1个体积为V1的球形液压缸和1根截面积为A1的连接管组成。装置设在推力轴承后面,推力轴承作用在减振器活塞上的力通过圆管内液体的惯性力、粘性阻力以及液压缸对液体的压缩力来平衡。经换算可以将该装置简化成一个虚拟的质量、弹簧和阻尼系统。系统的虚拟质量、弹簧和阻尼参数由装置的几何参数和内部液体决定,具体为:

(12)
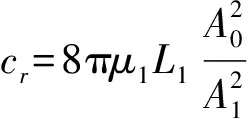
(13)
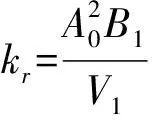
(14)
式中ρ1,μ1和B1分别为液体密度、动力粘性系数和体积模量。Goodwin认为当该装置的自振频率和桨轴系统的纵振固有频率相同时可以获得理想的减振效果。基于此,他提出当液压动力减振器的总质量为mr, 桨轴系统的第一阶纵振频率为fps, 虚拟刚度可取为:

(15)
虚拟阻尼系数可取为:

(16)
式中:

(17)
其中mp为考虑附连水的螺旋桨质量。
4 研究模型
研究一个双层加肋锥形壳钢结构,并假定内外壳间充满水,如图2所示,图中数字的单位均为m。
结构中to=0.016m,ti=0.030m,tr=0.010m,to,ti和tr分别为外壳、内壳和环肋的厚度。钢的材料参数为:弹性模量E=2.1E5MPa,泊松比ν=0.3,密度ρs=7 800kg/m3;水的材料参数为:v=1 450m/s, 密度ρw=1 000kg/m3。
划分有限单元时,板壳用四边形和三角形单元,内场水用六面体单元,且保证流体单元节点和对应结构单元节点空间位置重合。为模拟螺旋桨纵向激振传递过程,模型中还建了一个简单的桨轴系统,包括轴系、螺旋桨和推力轴承。轴线总长19m,环型截面,外径ro=0.225 m,内径ri=0.100 m;螺旋桨质量为Mp=20 000 kg;推力轴承刚度为K=1.50E10 N/m。轴系、螺旋桨和推力轴承分别用梁单元、质量点单元和弹簧单元模拟,有限元模型如图3所示。

图2 模型半纵剖面Fig.2 Half longitudinal section of the model

图3 结构有限元模型Fig.3 FEM model of the structure

图4 系统连接简图Fig.4 Sketch of connections between subsystems
研究分有无减振器2种情况。无减振器时推力轴承一端与推进轴连接,另一端通过多点约束与主结构连接;有减振器时,推力轴承后连减振器,减振器另一端通过多点约束和主结构连接,减振器用弹簧振子模拟。实际中可通过合理设计将减振器整合到推力轴承中,使推力块与机构中的活塞相连以实现减振目的。具体的连接关系如图4所示。根据Goodwin的方法来确定液压减振器的3个虚拟参数,首先要得到桨轴系统的一阶纵振频率。桨轴系统的固有频率是基于图4(b)模型计算的。通过有限元计算,得到轴系系统的前两阶纵振频率分别为21.4 Hz和97.7 Hz。若mr=1 000 kg,则由式(15)和式(16)可得到kr=1.81E7 N/m,cr=2.12E6 kg/s。引入减振器后轴系系统的前两阶纵振频率分别为3.3 Hz和85.9 Hz。
5 计算分析
对有无减振器2种情况进行谐相应振动分析。计算激励是幅值为4 000 N的纵向正弦力,作用在螺旋桨质心位置,计算频域为1~200 Hz,步长1 Hz。用虚拟质量法计入外场水对振动的耦合影响,具体的做法见文献[8]。计算采用模态叠加法,结构模态阻尼取0.03,忽略流体阻尼,提取结构和流体300 Hz以内的所有模态进行计算。为模拟潜艇自由浮在水中的状态,对艇体不施加任何约束。
图5和图6是圆锥壳的前两阶整体模态的振型,表1中列出了几种不同计算模型对应这两阶模态的固有频率。

图5 整体一阶模态Fig.5 First mode of the whole structure

图6 整体二阶模态Fig.6 First mode of the whole structure
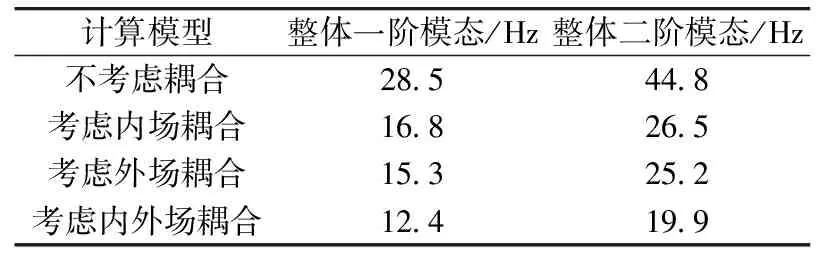
计算模型整体一阶模态/Hz整体二阶模态/Hz不考虑耦合285448考虑内场耦合168265考虑外场耦合153252考虑内外场耦合124199
从表中可知考虑了流固耦合作用后结构的固有频率大大降低,内外场流体对结构的影响都很大,任何一种耦合作用的缺失都将使振动特性和响应分析的结果失实。
振动响应计算完成后,提取表面振动响应作为边界元计算输入,在Sysnoise中计算结构的辐射声功率,图7是相应的辐射声功率级曲线。从图上看,引入减振器后结构的辐射声功率几乎在整个频段内都有不同程度的降低。从结果来看,在非共振频率处普遍有5~10 dB收益,在原模型一阶共振频点20 Hz附近声功率降幅更是在15~43 dB之间,二阶共振点97附近也有10~19 dB的下降。从趋势上看,引入减振器后结构响应的变化规律基本是不变的,减振器并不能改变结构声辐射的规律特性,只是由于减振器的存在使得轴系系统的固有频率有所降低,响应峰值有些向前迁移。由此可见,液压减振器对降低轴系纵振引起的声辐射非常有效。

图7 有无减振器模型声功率级曲线Fig.7 SPL curves of the models with and without vibration absorber
6 动力减振器参数优化
Goodwin的减振器设计方法物理意义明确,计算也显示效果明显。然而,该方法也有其问题。首先,它是对理想模型分析得到的,考虑到实际结构的复杂性不一定能获得最佳的减振效果;其次,该方法可能导致实际装置几何尺寸过大或过小,从而无法实现。本节将对液压动力减振器的3个虚拟参数进行优化,在可行域内寻找更好的参数组合。
从振动传递路径上看,螺旋桨激励是通过减振器传递给艇体的,这里取计算频域内减振器与艇体连接节点的平均加速度作为目标函数,变量为3个虚拟参数,优化目标是使目标函数值最小。

图8 优化模型示意图Fig.8 Sketch of the optimization model
由于壳体的流固耦合对轴系振动影响不大以及计算时间成本问题,优化时计算模型不考虑壳体的流固耦合作用。优化方案的数学表达式为:
Min[Avr(Acc)], 1 (18) 式中:Acc为考察节点处的加速度响应;Avr(Acc)为计算频段的平均加速度。 考虑到方案的可行性,根据文献[6]的经验,将3个参数的取值范围约束在: (19) 优化在Isight优化平台上进行,采用的是多岛遗传法。表2是优化后得到虚拟参数选取方案。 表2 动力减振器优化参数方案 由以上参数,根据式(14)~式(16)可以计算减振装置的具体几何尺寸。根据一般液压油的物理性质,假定液压油密度ρ1=900 kg/m3,动力粘性系数μ1=0.4 Pas,体积模量B1=1.8e9 Pa,若设计连管长L1=1 m,则可以算出圆柱油缸半径r0=104.9 mm,连管半径r1=18.5 mm,球形液压缸半径r=266.0 mm。这样的结构尺度在实际中可以做到。 图9是几种模型的激励传递点处的加速度级响应曲线。显然,引入Goodwin减振器后激励传递点在共振频点处的响应值大幅减小,但其他频率处降低并不明显。值得注意的是,由于此时减振器的阻尼系数很高一阶共振被遏制,所以图中没有明显的一阶共振峰。优化后,响应值除在一阶共振点处较其他模型略有升高外,其他频段均有很大幅度的下降。图10显示了优化前后结构辐射声功率级曲线。总体上看,结构响应变化趋势基本一致,除个点外优化后结构的辐射声功率较Goodwin方案又有了进一步的降低,降幅普遍都在20~30 dB之间,优化效果非常明显。可见,本文提出的优化方案不仅可行而且十分有效。 图9 优化前后的加速度响应Fig.9 Acceleration responses before and after optimization 图10 优化后的声功率级Fig.10 SPL before and after optimization 由以上分析可以得出以下结论: 1)联合使用虚拟质量法和常规的有限元方法模拟水下内外场耦合振动可行,忽略任何一种耦合作用的振动特性和响应分析结果都会与实际产生较大偏差。 2)基于Goodwin理论的液压动力减振器能有效地降低轴系纵振引起的船体表面辐射声功率。 3)用本文提出的优化方法对减振器参数进行优化,能够获得较Goodwin方案更好的减振降噪效果。 [1] 商德江,何祚镛.加肋双层圆柱壳振动声辐射数值计算分析[J]. 声学学报,2001,26(3):193-201. SHANG De-jiang,HE Za-yong.The numerical analysis of sound and vibration from a ring-stiffened cylindrical double-shell by FEM and BEM[J].Acta Acvstica,2001,26(3):193-201. [2] 姚熊亮,刘庆杰,翁强,等.水下加筋圆柱壳体的振动与近场声辐射研究[J].中国舰船研究,2006,1(2):13-19. YAO Xiong-liang,LIU Qing-jie,WENG Qiang,et al.Research on the vibration and near field acoustic radiation of underwater ribbed cylindrical shell[J].Chinese Journal of Ship Research,2006,1(2):13-19. [3] 徐张明,汪玉,华宏星,等.船舶结构的建模及水下振动和辐射噪声的FEM/ BEM计算[J].船舶力学,2002,6(4):89-95. XU Zhang-ming,WANG Yu,HUA Hong-xing,et al.Modeling of the ship and numerical simulation of coupled vibro-acoustic behavior by FEM/BEM[J].Journal of Ship Mechanics,2002,6(4):89-95. [4] 刘晓明,王晓宇,陈慈慧.流固耦合船舶舱室中低频噪声数值分析,船舶力学,2008,12(5):812-818. LIU Xiao-ming,WANG Xiao-yu,CHEN Ci-hui.Numerical analysis of low and middle frequency noise in ship cabin using fluid-structure coupling[J].Journal of ship Mechanics,2008,12(5):812-818. [5] GOODWIN A J H.The design of a resonance changer to overcome excessive axial vibration of propeller shafting,Institute of Marine Engineers-Transactions,1960,72:37-63. [6] DYLEJKO P G.Optimum resonance changer for submerged vessel signature reduction,PhD Thesis,The University of New South Wales,Sydney,Australia,2008. [7] MSC.Nastran Version 70,Advanced Dynamic Analysis User′s Guide. [8] Fluid-structure analysis using MSC/Nastran. Vibration and acoustic analysis of a submerged conical double shell structure and vibration optimization XU Zhi-liang,WENG Zhang-zhuo (China Ship Design and Research Center,Wuhan 430064,China) Research on the vibration response a submerged conical double shell structure subjected to a sinusoidal longitudinal force from the propeller is made, with the combination of fluid-solid coupling FEM and virtual mass method, and using the BEM its sound radiation characteristics is got This method, union of the FEM and virtual method ,is very effective to analysis the problems concerning inner and outer filed coupling. This method avoided complex model construction of the fluid out of structure. Through calculation, the effectiveness of the so-called resonance changer, a hydraulic dynamic vibration absorber, in reducing sound radiation was proved. Further more , based on the theory method, a easy and feasible parameters optimization scheme of the absorber was proposed, through the optimization sound radiation power of the structure lowered more. fluid-solid coupling;virtual mass method;sound radiation power;hydraulic dynamic vibration absorber 2013-04-22; 2013-05-31 徐志亮(1986-),男,助理工程师,研究方向为结构振动噪声控制。 U661.44 A 1672-7649(2014)03-0019-05 10.3404/j.issn.1672-7649.2014.03.004


7 结 语
