An Approximate Method for the Surge Response of the Tension Leg Platform
2014-07-30RahimShoghiandMohammadRezaTabeshpour
Rahim Shoghi and Mohammad Reza Tabeshpour
1. Faculty of Civil Engineering, Tabriz University, Tabriz, Iran
2. Center of Excellence in Hydrodynamics and Dynamics of Marine Vehicles, Mechanical Engineering Department,Sharif University of Technology, Tehran, Iran
1 Introduction1
The solution of the Duffing equation in a nonlinear vibration problem is studied in this paper. With the rapid development of nonlinear science, there has appeared an ever increasing interest from scientists and engineers in the analytical techniques for nonlinear problems. The widely applied techniques are perturbation methods. But, like other nonlinear analytical techniques, perturbation methods have their own limitations. The governing equation for the problem was formulated by Nayfehet al. (1978) and Nayfeh(1981). In the case of the perturb parameter being small, the equation is solved using the Lindstedt–Poincare technique,the method of multiple scales, and the method of averaging that was presented by Nayfehet al. (1978) and Nayfeh (1981).Almost all the perturbation methods are based on small parameters so that the approximate solutions can be expressed in a series of small parameters. The limitation of the perturbation method was pointed out by He (1998) and(2000). Clearly, in the case of the perturb parameter being a larger value, the traditional perturbation method is no longer valid but the Homotopy perturbation method (HPM) is usually applicable as presented by He (1999).
An elementary introduction to some new asymptotic methods for the search for the solitary solutions of nonlinear differential equations,nonlinear differential-difference equations, and nonlinear fractional differential equations is presented by He (2012). He(2012) suggests an alternative approach to the construction of the homotopy equation with an auxiliary term. Surveys of some recent developments in asymptotic techniques which are valid not only for weakly nonlinear equations, but also for strong ones are presented by He (2006). Many studies have been carried out to understand the structural behavior of moored structures to determine the effects of several parameters on the dynamic response and average life time of the structure. Dynamic analysis of a triangular model tension leg platform (TLP) to a regular wave, considering the coupling between a surge, sway, heave, roll, pitch and yaw degrees-of-freedom is presented by Chandrasekaran(2002). The dynamic motion responses of an offshore semi-submersible platform in regular sea waves obtained by applying numerical time domain dynamic integration using the Morison equation in the first case and diffraction theory in the second case was presented by Kurianet al. (2010). Perturbation solutions for axial vibrations of tension leg platforms were presented in order to study the higher order effects on heave response.
The dynamic response of the tether of a Tension Leg Platform, subjected to an axial load at the top of the leg, was presented by Golafshaniet al. (2007). The effects of the added mass fluctuation on the vertical vibrations of the tension leg platforms in the case of vibrations in still water for both free and forced vibrations subjected to an axial load at the top of the leg was presented by Tabeshpour et al.(2006). They used the perturbation method to formulate and solve the problem. Firstand second-order perturbations are used to solve the free and forced vibrations, respectively.Conceptual discussions on the free vibration analysis of TLP has been presented by Tabeshpour (2013) giving an in-depth andpractical view of the structural dynamic responses for both analysis and design purposes. Comparing the dynamic motion responses of a TLP in regular sea waves obtained by applying three methods in time domain using MATLAB software has been investigated by Tabeshpour and Shoghi(2012). The results were obtained as responses represent good accordance between results of the close form(analytical) method and the numerical method.
HPM is used to solve weak and strong nonlinear differential equations for finding the perturbed frequency of response. Calculated responses by approximate method are compared with responses obtained from the Numerical method for time history of the response and phase plane.The Numerical method of the modified Euler method (MEM)is used to solve the Duffing equation, which is acceptable for solving nonlinear differential equations. Some of the differences between a linear system and a nonlinear system are presented by Kelly (1996) :
(1) The behavior of a nonlinear system is governed by a nonlinear differential equation. Exact solutions do not exist for many nonlinear differential equations.
(2) A nonlinear system may have more than one equilibrium point. An equilibrium point may be stable or unstable.
(3) Steady·state behavior, if it exists for a nonlinear system, is dependent upon initial conditions.
(4) The period of free vibrations of a nonlinear system is dependent upon initial conditions. This implies that the frequency of free vibrations is dependent upon the free vibration amplitude.
(5) A nonlinear system exhibits resonance at excitation frequencies different from the system's linear natural frequency. A superharmonic resonance exists in a system with a cubic nonlinearity when the excitation frequency is one·third of the system's linear natural frequency. A subharmonic resonance exists when the excitation
frequency is nearly three times the system's linear natural frequency.
(6) The principle of linear superposition cannot be used to analyze a nonlinear system subject to a multifrequency excitation. A combination resonance can exist for appropriate combinations of excitation frequencies.
(7) Internal resonances can exist in multi-degree-of-freedom and continuous systems for appropriate combinations of natural frequencies.
(8) A periodic excitation may lead to a nonperiodic response in a nonlinear system. Such chaotic motion occurs in many nonlinear systems for certain parameter values.
2 Governing equation
Fig. 1 represents a TLP and its structural components.
Because the buoyancy of the TLP exceeds its weight, the vertical equilibrium of the platform requires taut moorings connecting the upper structure to the seabed. The extra buoyancy over the platform weight ensures that the tendons are always kept in tension. Fig. 2 represents a surge displacement of the TLP under wave force.
Springs have stiffness equal tok1andk3x2as linear and nonlinear respectively. That structural damping is assumed to be equal to zero. By giving an arbitrary displacement in thexdirection, the forces in each term of the spring take the form represented below. For linear and nonlinear force are as follows, respectively:

The amount of elastic force for a given displacement is expressed as follows:

k3is a very small quantity rather thank1, while nonlinear force due to nonlinear stiffness,, is remarkable in comparison to linear force,for a large value ofx.The potential energy function due to the presence of4xis not a parabolic shape. Different forms of power and potentials in the Fig. 3, for systems with large displacement(worked in nonlinear) are shown.
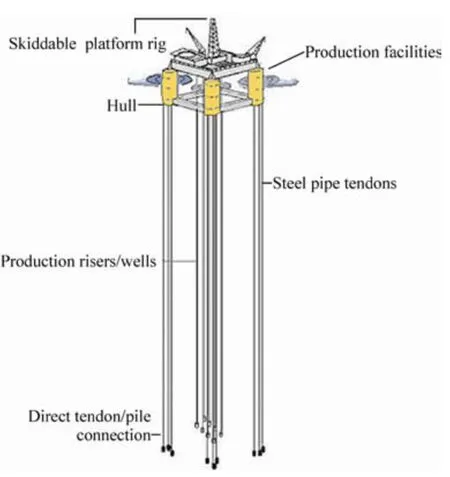
Fig. 1 Structural modeling of TLP (internet)

Fig. 2 Arbitrary TLP displacement via wave force

Fig. 3 Mechanical model of the SDOF TLP in the surge direction
Considering the equilibrium equation of motion, the equation of motion inxdirection under the initial boundary condition takes the form of:

Rewrite Eq. (6) as follows:
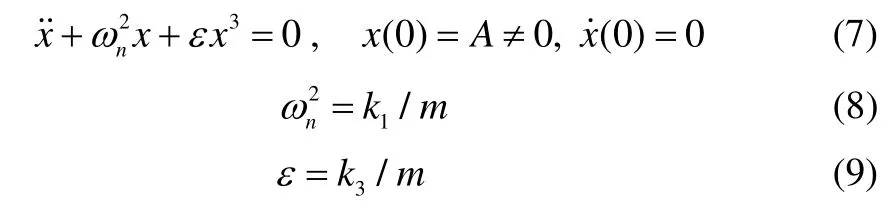
whereωnis the circular frequency, andεis a constant which may not be a small value.

Fig. 4 Power and potential function for systems with a nonlinear spring
2 Homotopy perturbation method
The HPM divides the equation into two parts, whereL(x) is linear, whileN(x) is the nonlinear part of it and therefore, can be rewritten as follows:

A solution in the form of an infinite series of the perturbation parameterpis assumed as follows:
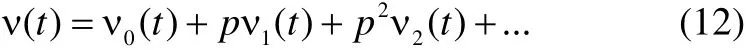
Finally, with the following limit approximate response of Eq.(7) is obtained:
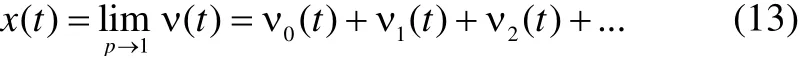
Eq.(13) indicates a better accordance response of HPM and MEM in the case of considering more terms as the final response in Eq.(9). Writing the Homotopy Perturbation function:
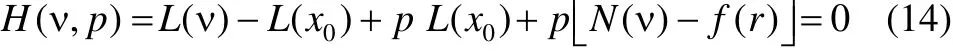
wheref(r) is a known analytic function that is equal to zero in the free vibration.x0is an initial approximation of Eq.(7),which satisfies the boundary conditions. Assuming initial approximation of Eq.(7) gives the following:

The perturb frequencyα(ε) is an unknown constant achieved from HPM under the conditionα(0)=ωn. The Acting Homotopy function for nonlinear systems as how accuracy is required, one obtaines the multi linear equation.Obtained equations are related as a chain. The response of each obtained equation is applied to the input of the next equations. Substituting Eqs.(12) and (15) into Eq.(14), the coefficients of the various powers ofpmust be equated to zero, then one obtains:
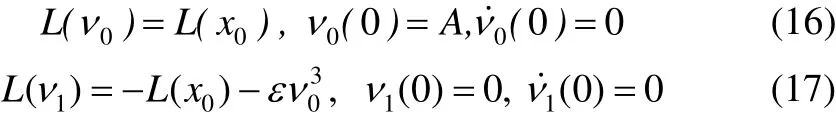
The solution of Eq.(16), subjected to the initial conditionsν0(0) = A and ν>gt;0 (0) =0, is:
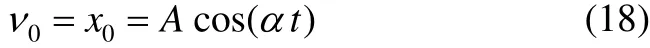
Eq.(17) is obtained from the Homotopy function.Substituting Eq.(18) as the input to the right hand side of Eq.(17), one obtains:
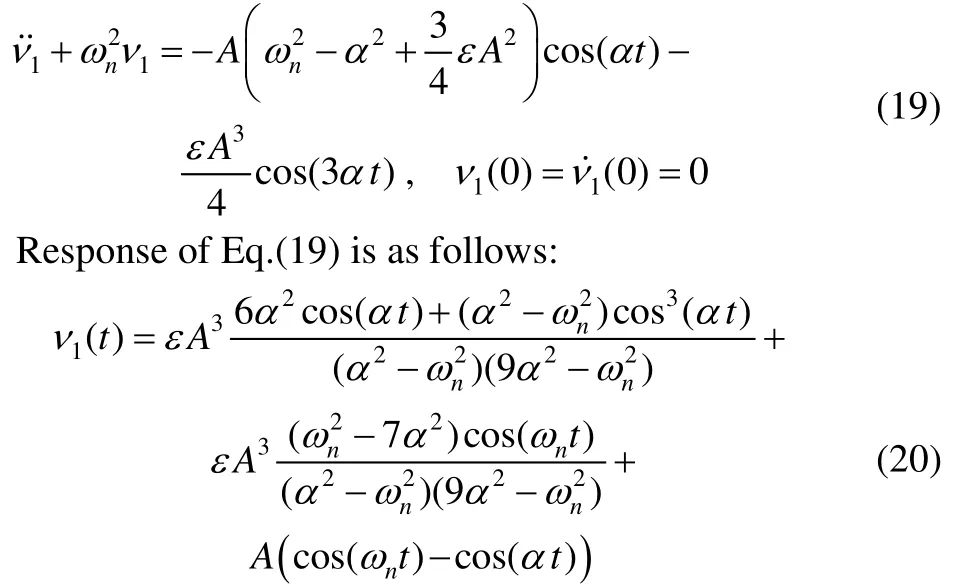
In order to eliminate the secular term which may occur in the next iteration, set the coefficient of cos( ωnt) in Eq.(20)to equal zero as follows:

αis obtained from Eq.(21-a) as follows:
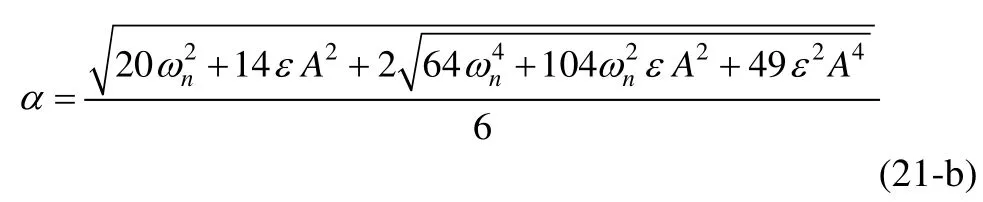
It is observed that in nonlinear systems, the amount of response frequency depends on the initial conditions and the perturbation parameter. Also assumingε=0 in Eq.(21-b),α=ωnis obtained.
3 Approximate method
The response of the linear part of Eq.(7) as the initial approximation of the Duffing equation which satisfies the boundary conditions is as follows:
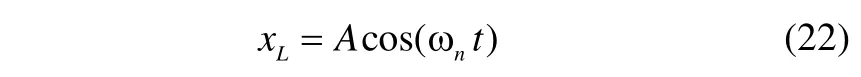
The rising in amplitude of the vibrations causes an increase in the force of the springs as shown in Eq.(3). The variable stiffness of the Duffing leads to changes in the frequency of the response. Considering the perturb frequency as follows, one obtaines:
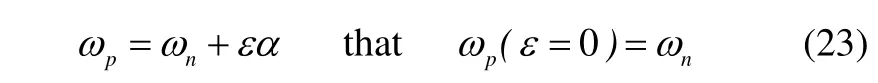
where α is the unknown constant. Considering Eq.(23) the initial approximation of the Duffing is as follows:

whereis an approximation of the Duffing equation response, which satisfies the following conditions in the time line.

Replacing Eq.(24) into the Error condition, one can obtain:
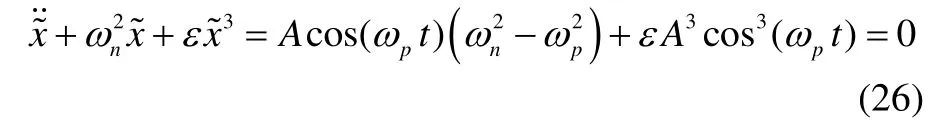
Using:
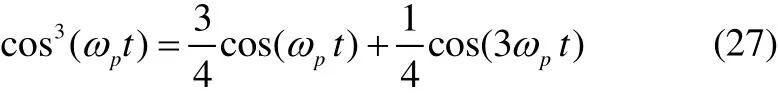
Fig. 5 represents the component of Eq.(27) forT=1s.
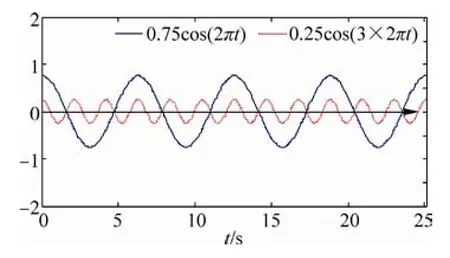
Fig. 5 Component of Eq. (27) for T=1s
Considering the above figure, cos(3ωp t) is ignored in the contrast cos(ωp t). Rewriting Eq.(26) in the form:
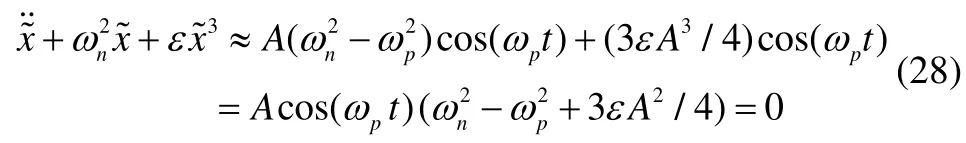
Substitutingω p=ω n+εαinto Eq. (28),αis achieved:
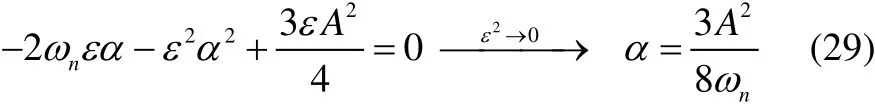
Substituting α in Eq.(23), perturb frequency is achieved as follows:
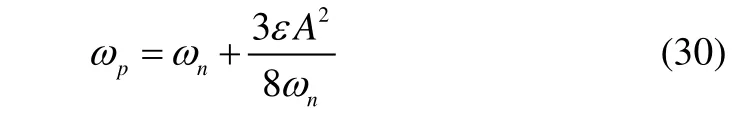
The nonlinear term of the Duffing approximate solution of Eq.(24) is achieves as follows:
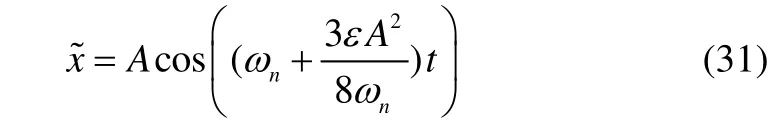
A numerical study has been carried out to compare the obtained frequencies. It is supposed thatωn=1,m=1,perturbation parameterε= 0.01, 0.05 and 0.1 for different initial conditions. Verification of the obtained perturb frequency and responses are carried out by HPM and the numerical method respectively.
Table 1 represents good accordance between the frequencies from the approximate method and HPM.
The Figs 6-8 represent acceptable accordance between the achieved results of the approximate method and numerical method in amplitude and frequency content.

Table 1 Perturbed frequencies for ω n=1
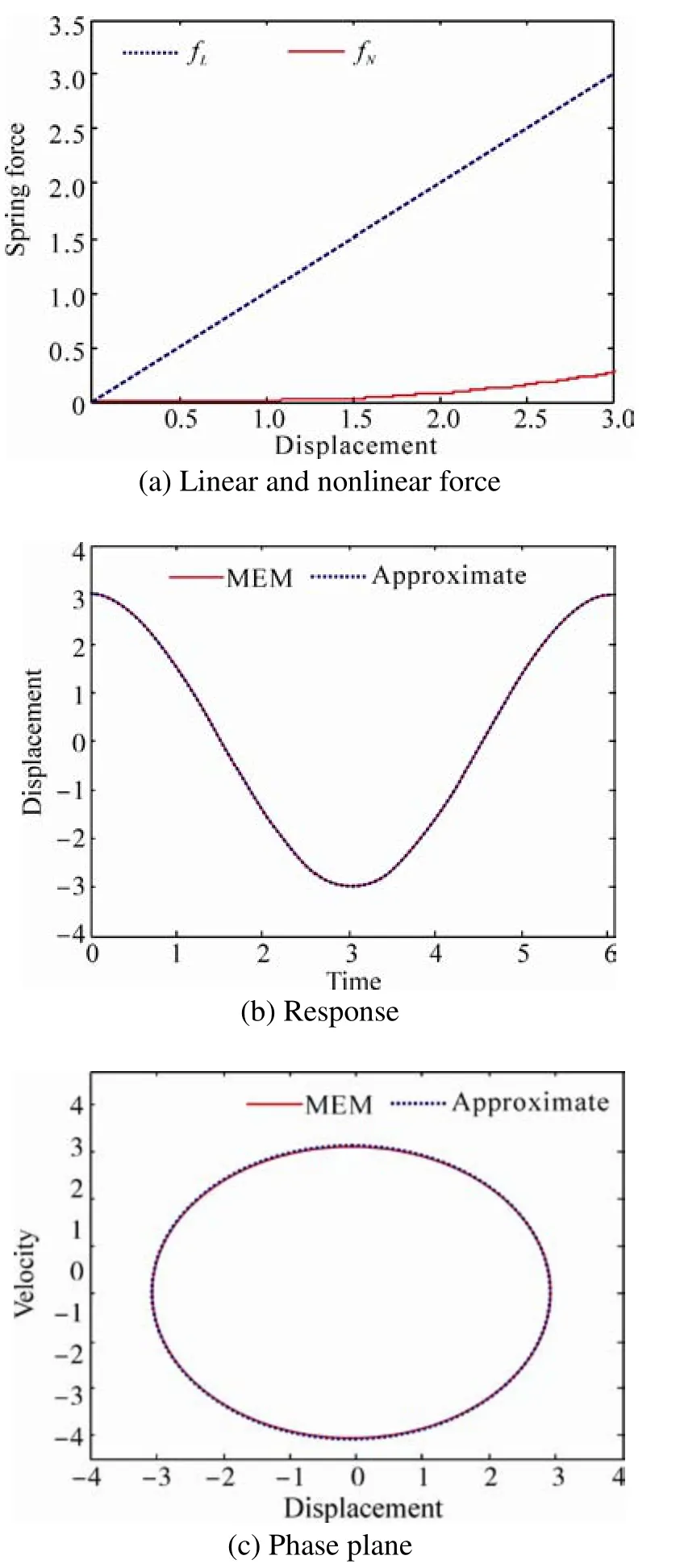
Fig.6 comparing exact and approximate method for: ωn=1,ε=0.01, A=3
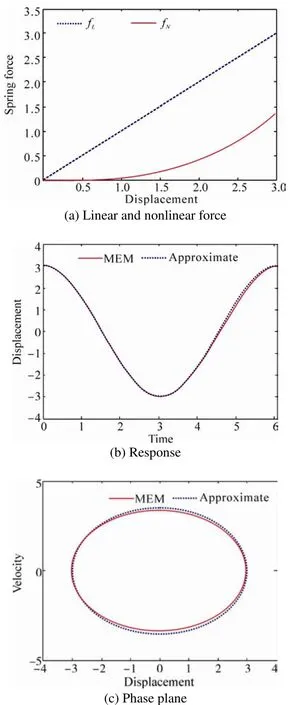
Fig. 7 comparing exact and approximate method for: ωn=1,ε=0.05, A=3
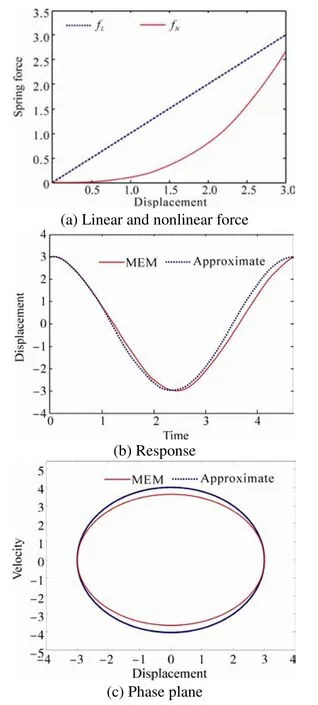
Fig. 8 comparing exact and approximate method for: ωn=1,ε=0.05, A=3
4 Conclusion
From the above analysis, it is observed that none of the mentioned properties (response, frequency, spring forces,velocity) of motion are independent, and they are derived from the mentioned equation and initial condition. The aim of this study is to derive an approximate motion such that:
The trajectory in the approximate motion on the phase plane is very close to the one defined by MEM.
The approximate response satisfies the boundary conditions exactly.
The approximate motion may not satisfy governing Eq.(25) exactly.
It is observed that the circular frequencyωpin the approximate motion is close to the obtained circular frequency via HPM of the Duffing equation.
Chandrasekaran S, Jain AK (2002). Dynamic behaviour of square and triangular offshore tension leg platforms under regular wave loads.Ocean Engineering, 29(3), 279–313.
Golafshani AA, Tabeshpour MR, Seif MS (2007). First order perturbation solution for axial vibration of tension leg platforms.Scientia Iranica, 14(5), 414-423.
He JH (1998). Approximate solution of nonlinear differential equations with convolution product nonlinearities.Computer Methods in Applied Mechanics and Engineering, 167(1),69-73.
He JH (1999). Homotopy perturbation technique.Computer methods in applied Mechanics and Engineering, 178(3),257-262.
He JH (2000). A coupling method of a homotopy technique and a perturbation technique for nonlinear problems.International Journal of Nonlinear Mechanics, 35(2000), 37–43.
He JH (2006). Some asymptotic methods for strongly nonlinear equations.International Journal of Modern Physics B,
20(2006),1141-1199.
He JH (2012). Asymptotic methods for solitary solutions and compactons.Abstract and Applied Analysis, 2012(2012),Article ID 916793.
He JH (2012). Homotopy Perturbation Method with an Auxiliary Term.Abstract and Applied Analysis, 2012(2012), Article ID 857612.
http://www.offshore-technology.com/projects/glider/glider1.html.
Kelli SG (1996).Theory and Problems of Mechanical Vibrations,McGraw-Hill, New York.
Kurian VJ, Ng CY, Yassir MA (2010). Response of semi-submersible platform by Morison equation and diffraction theory.World Engineering Congress, Perak, Malaysia.
Nayfeh AH, Mook DT (1978).Non-linear Oscillations.Wiley,New York.
Nayfeh AH (1981).Introduction to Perturbation Techniques.Wiley, New York.
Tabeshpour MR, Golafshani AA, Seif MS (2006). Second-order perturbation added mass fluctuation on vertical vibration of tension leg platforms. Marine Structures, 19(4), 271-283.
Tabeshpour MR, Shoghi R (2012). Comparison between linear and non-linear models for surge motion of TLP.International Journal of Marine Science and Engineering, 3, 153-162.
Tabeshpour MR (2013). Conceptual discussion on free vibration analysis of tension leg platforms.Development and Applications of Oceanic Engineering (DAOE), 2(2), 45-53.
杂志排行
Journal of Marine Science and Application的其它文章
- Hard Foulers Induced Crevice Corrosion of HSLA Steel in the Coastal Waters of the Gulf of Mannar (Bay of Bengal), India
- CFD Simulation of the Vertical Motion Characteristics of the Moonpool Fluid for the Truss Spar
- Dynamic Coupled Analysis of the Floating Platform Using the Asynchronous Coupling Algorithm
- Numerical Investigation of Mooring Line Damping and the Drag Coefficients of Studless Chain Links
- Floating Production Platforms and their Applications in the Development of Oil and Gas Fields in the South China Sea
- Bucket Group Effect of the Composite Multi-bucket Structure
