Strength Reliability Analysis of Stiffened Cylindrical Shells Considering Failure Correlation

Xu Bai, Liping Sun, Wei Qin and Yongkun Lv

1. School of Naval Architecture >amp; Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China

2. Deepwater Engineering Research Center, Harbin Engineering University, Harbin 150001, China

3. Technical Institute, COSCO (Dalian) Shipyard Co., Ltd., Dalian 116113, China

1 Introduction1

Stiffened cylindrical shells are widely used in the pressure hulls of submarines and submersibles, platform legs and hold-up vessels, etc. The design problems of these kinds of structures have been a subject of interest over the last several decades and still extensively researched nowadays. Despite the higher technological requirements under construction, the structural failure risk of the stiffened cylindrical shells still exists because of the complex of structural size and material property, reliability of calculation model and uncertainty of machining errors (Bhattacharyaet al., 2001). Generally, the deterministic approaches decrease the uncertain factors by using the “safety coefficient” and the method of reliability is more accurate and trustworthy by considering the uncertain factors quantitatively.

Some research on the reliability of the stiffened cylinder has been conducted. The system reliability of the submarine pressure stiffened cylindrical shells with immediate integration was analyzed and calculated in the paper written by Yuet al. (2012) and by Gaytonet al. (2003). An adaptive radial-based importance sampling method for structural reliability was presented in the paper written by Grooteman(2008). The research on the neural network and response surface for structural reliability analysis was presented by Herbertet al. (2004). Reliability-based structural optimization using the neural network and Monte Carlo simulation was reported by Papadrakakis and Lagaros (2002) ; Deng and Gu(2005). Zoul and Mahadevan (2006) provided a direct decoupling approach for efficient reliability-based design optimization. A large amount of valuable discussion was conducted for the construction of the structure failure modes and the selection of the calculation methods to analyze the data and determine the sensitivity factors, specific to the system reliability of the ring-stiffened cylinder. Correlation between failure modes was not discussed in the above literatures.

There are many failure modes in stiffened cylinder shells and each failure mode correlates to another. The correlation between failure modes has a certain impact on the reliability index and failure probability of the structural system.Correlations between failure modes will work when identical random variables appear in different performance functions.Certainly, the correlation coefficients among different failure modes are different, which leads to the difference of effect of correlation on system reliability. The understanding of the correlation on stiffened cylindrical shells is necessary to quantitatively research the influence on the correlation regarding system reliability. In order to simplify the problem,the correlations between the random variables are ignored.

The impact of each factor on structural reliability is an important part in researching structural integrity. If some factors greatly affect reliability, it is required to provide relatively accurate data; otherwise the factors can be treated as a constant to improve the calculation efficiency. Therefore,this paper analyzes the correlation between static strength failure modes of stiffened cylinders with a generalized reliability index. The calculation of the reliability of the system static strength is discussed and an approximate analysis method of the system reliability of stiffened cylinders under hydrostatic pressure has been gained.

2 Static strength reliability mode of stiffened cylindrical shells

According to the load-strength interference theory, it is the load beyond its strength that leads to the damage of the structural unit. Structural reliability is the effect of two contradictory reactions between unit performance and the environment load in the probability measure space. The safety margin equation of structural static strength is:

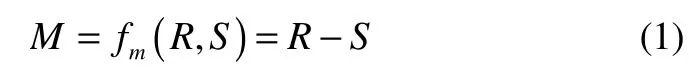
The mean and standard deviation in the form:

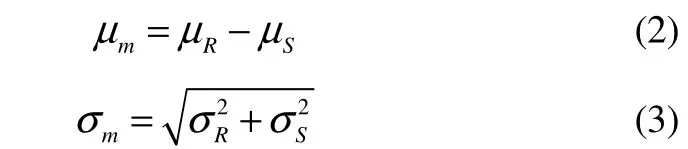
whereRis the strength and is representative of the steel lowest yielding point;Sthe stress and is representative of the real internal force of the structure.

Then, the reliability index can be expressed as:

The limit state equation is nonlinear when the structural resistance and load do not follow the normal distribution;therefore, it is needed to linearize the equation before calculating the reliability index.

There are three kinds of strength failure modes with stiffened cylindrical shells under hydrostatic pressure. The reliability mode of the stiffened cylindrical shells can be established due to the relationship within the above reliability index.

The first kind of failure mode is the shell failure between ribs of stiffened cylindrical shells. The mean and standard deviation of the shell’s mid-plane stress in the middle of the ribs can be expressed as:

Refer to the study of Ma (2009), it is safe while, so the limit state equation of the failure modes is:

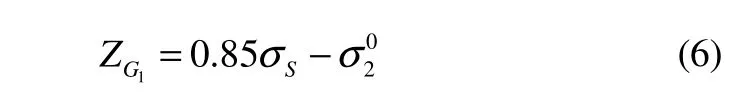
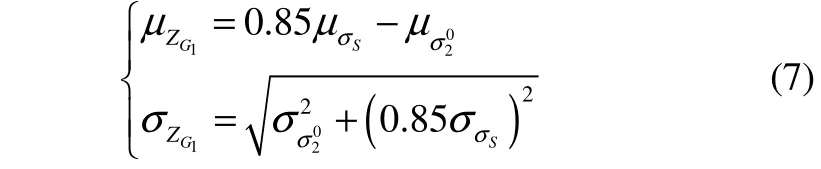
where,σσSis the standard deviation of the material yield strength is;σμSthe mean deviation.

So:

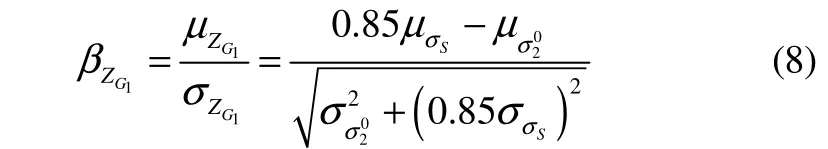
The second kind of failure mode is shell failure which is in the position of the ribs of the stiffened cylindrical shells. The mean and standard deviation of the shell longitudinal stress near the end ribs can be expressed as:

where,1σμis the mean of the mid plane gravitation;1σσthe standard deviation of the mid place gravitation;1Kthe safety factor.

It is safe whileσ1≤ 1.15σS,so the limit state equation of the failure modes is:

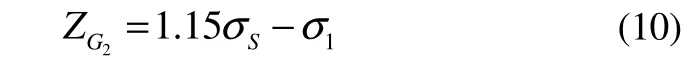
where,σS,1σandZ2Gare the normal distribution, then:

So:

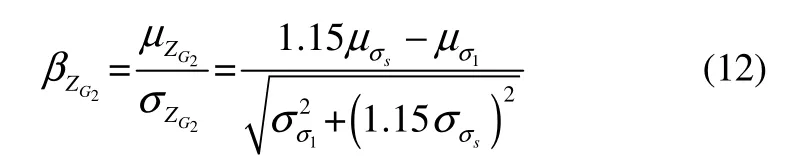
The third kind of failure mode is the rib failure of stiffened cylindrical shells. The mean and standard deviation of frame stress on the ring-stiffened cylinder can be expressed as:

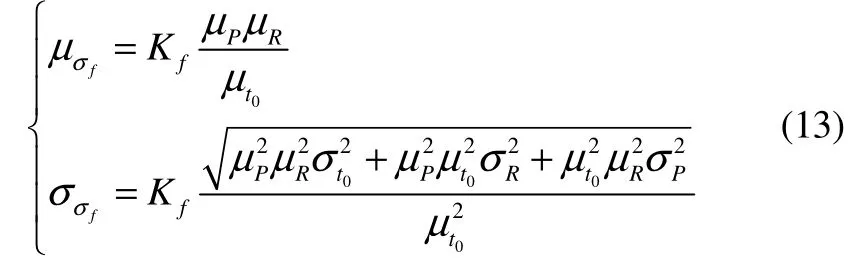
where,μGfandμ1Gare the means of the mid plane gravitation;σσfand1σσthe standard deviations of the mid plane gravitation;Kfthe safety factor.

It is safe whileσf≤0.6σS, so the limit state equation of the failure modes is:

where,σS,σ fandZ3Gare the normal distributions, then:

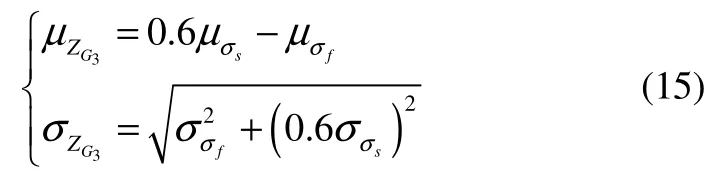
So:

3 Analyses on the correlation between failure modes

While the structural performance function is nonlinear,assume that all the random variables are a normal distribution and statistically independent. So, calculate the correlation coefficient by the first-order of the Taylor series expansion atX*:

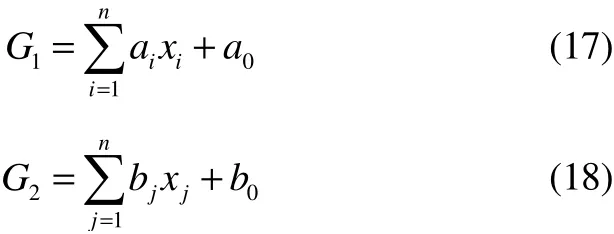
where,ai,bi(i=0,1,…,n) are constants andXi(i=1,2,..,n) are a set of independent random variables and the mean isμXi, the variance isσXi. It is easy to get the mean and standard deviation of the two failure modes, denoted asμ1GandμG2,the correlation coefficient is:

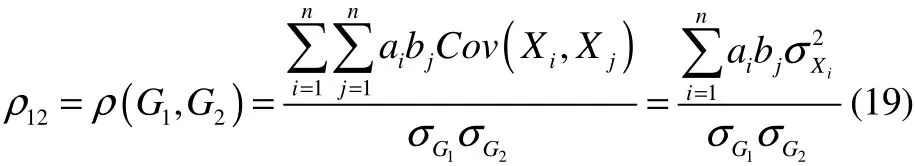
The reliability index vector ofG1andG2are:

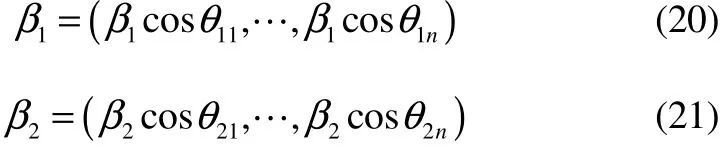
Obviously:

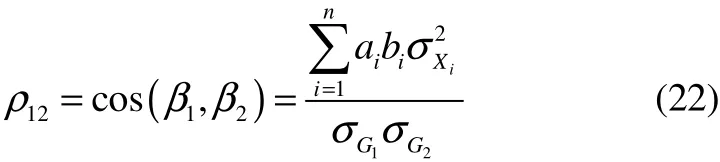
For multiple failure modes, the written reliability index of every failure mode as1β, the correlation coefficients of failure modes are:

4 Structural system reliability of stiffened cylindrical shells

The whole structural system of the stiffened cylinder is in a failure state no matter if any failure mode occurs. So the stochastic structural system used in analyzing the reliability of the stiffened cylindrical shell can be regarded as a tandem system, as it is shown in Fig. 1.

Fig. 1 Reliability model of the tandem structure system

Therefore, the failure probability of the structural system of the stiffened cylinder is:

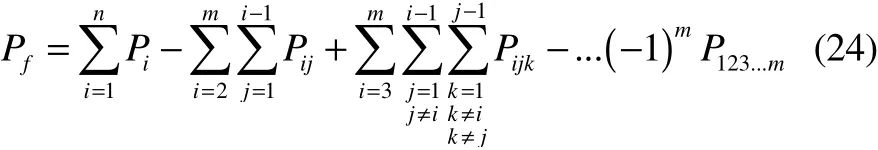
where,iPis the failure probability of failure modeiin the tandem system;ijPthe joint failure probability between the failure modesiandj;P123...mthe joint failure probability among failure modesi,jandm.

Eq.(23) represents the accurate value of the failure probability in the tandem system with failure modes numbern. The more failure modes considered in the calculation, the higher order of the joint failure probability will be applied,and the more accurate the calculation results of the structural failure probability will be. At the same time, the amount of computation is larger too. Generally, only the second order can be used for the purpose of simplifying the complexity,and the formula can be expressed as:

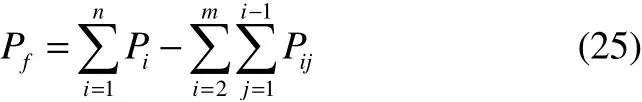
The joint probability density function of the two-dimensional normal distribution is:

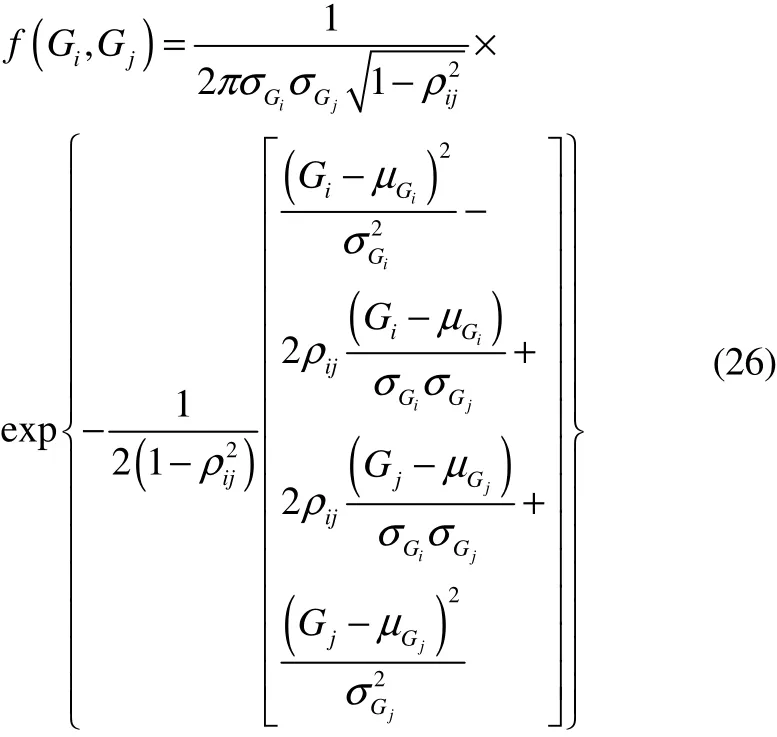
Therefore the second order joint failure probability is:

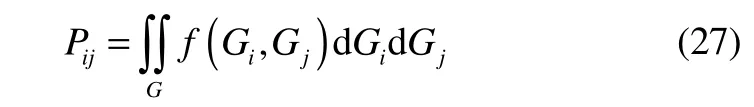
whereGis the integral area, as shown in Fig. 2.

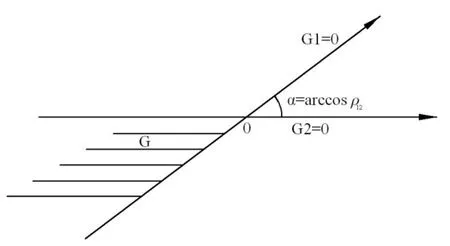
Fig. 2 Integral area of 2D joint failure mode

In Fig. 2, the 2D joint failure probabilities are trending to zero in the area far away from the origin coordinates. Su(2012) and Cheng (2004) presented a simplified calculation method for solving the two-dimensional integral. SoGis equivalent to the shaded areain figure 3.In that paper,was expressed as:

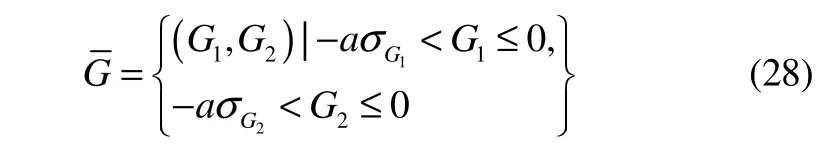
Divide the shaded area along the sides−aσG1and−aσG2intobparts respectively, and the area will be divided intob2parts. So,P12can be expressed as the sum of each small area multiplying its joint probability density:

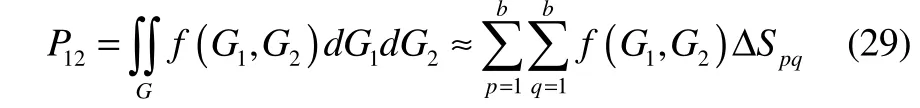
where, ΔSpqis the area of each segment;f(G1,G2) the joint probability density in the middle of each segment, and:

Fig. 3 The main integral area

5 Reliability analysis considering correlation

There are a lot of factors that affect the structural strength of the stiffened cylinder, such as material property, structural dimensions, etc. This paper analyzes the strength reliability of the stiffened cylindrical shell structural system, and takes geometric size and material yield strength as random variables, and other variables as determinate variables. The structural parameters and statistical characteristics are determined after referring to a large number of literature, as shown in Table 1.

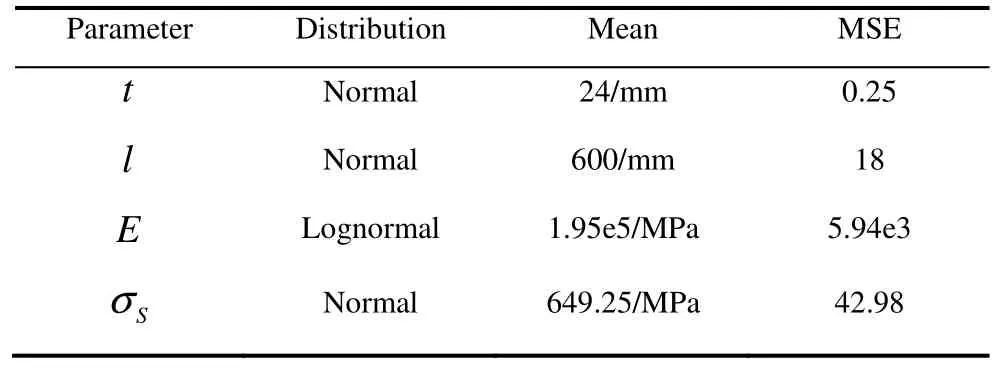
Table 1 Structure parameters and its statistical characteristics of stiffened cylindrical shells

In this section, the failure modes of shell failure between the ribs of stiffened cylindrical shells, shell failure which is in the position of the ribs of the stiffened cylindrical shells and rib failure of the stiffened cylindrical shells are respectively defined asG1,G2andG3. The MATLAB software is used to write programs through formulas in section 1 and for making calculations. The reliability indexes of three failure modes are gotten, and the values are shown in Table 2.

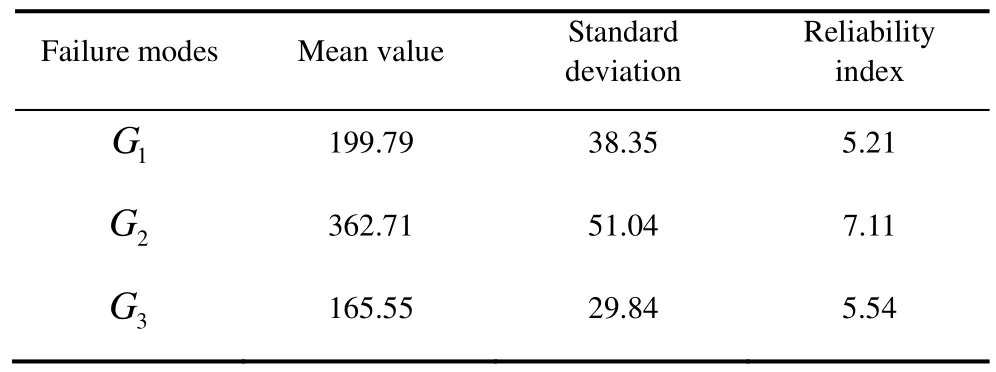
Table 2 Reliability index of failure modes of stiffened cylindrical shells

According to the calculation method for determining correlations between failure modes in Section 2, Table 3 shows the correlation coefficients among the failure modes.

Table 3 Correlation coefficients of the failure modes with static strength

And then the joint failure probability ofG1,G2andG3are gotten from the values in Table 3 and the calculation method in section 3. The results are shown in Table 4.

Table 4 The joint probability related to failure modes

In Table 4, the joint failure probabilities among failure modes trending to zero were received through comparison with the failure probability of the mode. Therefore, the failure probability of the whole stiffened cylinder structural system is the sum of each failure probability of every failure mode. Meanwhile, this conclusion is quite consistent with the results in the thesis of Ma (2009). Then, the Monte Carlo Simulation was used to verify the calculation results.

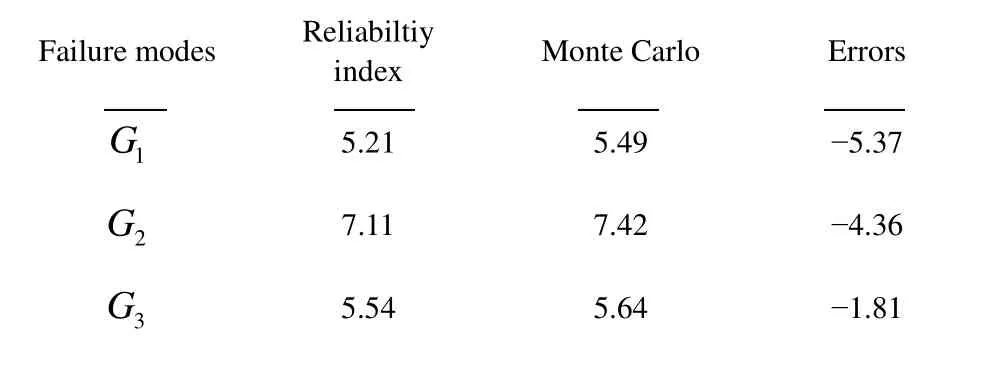
Table 5 The comparison of simulation and calculation results

In Table 5, the method of this paper is demonstrated to be able tosatisfy the precision of the strength reliability calculations of the structural system and the joint failure probability of the failure mode can be expressed directly. It is advantageous to the structural design based on reliability.

6 Conclusion

This paper presents an approach to analyze the structural reliability of cylindrical shells considering the correlation between failure modes.

The strength reliability modes was established through the load-strength interference theory. The calculation formula for the correlation between failure modes was derived. In additon, the joint failure probabilities of the 2D failure modes based on correlations among failure modes were obtained. The accuracy of the system reliability calculation was verified through use of the Monte Carlo simulation.According to the results of the research data analysis, the failure probability of stiffened cylindrical shells can be gotten through adding the failure proability of each mode.

The results can serve as a valuable reference for optimum designers of cylindrical shells. In our future work, the effect of the correlations between different failure modes will be systematically and comprehesively discussed.

Acknowledgements

The authors would like to thank Professor Xiaotian Wang of Harbin Engineering University for his help throughout the course of this study and express their gratitude and sincere appreciation to the anonymous reviewers for constructive suggestions on how to improve the quality and readability of this paper.

Bhattacharya B, Basu R, Ma KT (2001). Developing target reliability for novel structures: the case of the Mobile Offshore Base. Marine Structures, 14, 37-58.

Cheng YS, Au FTK, Tham LG, Zeng GW (2004). Optimal and robust design of docking blocks with uncertainty.Engineering Structure, 26, 499-510.

Deng Jian, Gu Desheng (2005). Structural reliability analysis for implicit performance functions using artificial neural network.

Structure Safety, 27, 25-48.

Gayton N, Bourinet JM, Lemaire M (2003). CQ2RS: a new statistical approach to the response surface methods for reliability analysis.Structure Safety, 25, 99-121.

Grooteman F (2008). Adaptive radial-based importance sampling method for structural reliability.Structural Safety, 30, 533-542.Herbert MG, Armando MA (2004). Comparison of response surface and neural network with other methods of structural reliability analysis.Structure Safety, 26, 49-67.

Ma Yongliang (2009). Reliability assessment of submarine structure considering corrosion. Master thesis, Harbin Engineering University, 30-38.

Papadrakakis M, Lagaros ND (2002). Reliability-based structural optimization using neural networks and Monte Carlo simulation.

Computer Methods in Applied Mechanics and Engineering,

192(32), 3491-3507.

Su Changqing, Zhang Yimin, Du Jinsong (2012). Frequency reliability analysis of rotor system with correlation failure modes.Journal of Mechanical Engineering, 48(6), 175-179.

Yu Yingxia, Liu Fengjun, Zhang Wei, Liang Bin (2012).Improving of RSM-FORM and application to reliability calculation of ring-stiffened cylindrical shell.Journal of Ship Mechanics, 16(3), 271-276.

Zoul T, Mahadevan S (2006). A direct decoupling approach for efficient reliability-based design optimization.Structural and Multidisciplinary Optimization, 31(3), 190-200.