Modeling of Fully Nonlinear Wave Radiation by Submerged Moving Structures Using the Higher Order Boundary Element Method

M.A. Hannan, W. Bai and K.K. Ang

Department of Civil and Environmental Engineering, National University of Singapore, Kent Ridge, Singapore 117576, Singapore

1 Introduction1

The interaction between submerged bodies and regular surface waves has been studied analytically, experimentally and numerically by many authors and for many years.However, in recent years the renewed interest in using ocean renewable energy and, in particular, wave energy demands more comprehensive studies of the interaction between submerged structures and water waves. Because for many offshore engineering applications, namely submerged breakwaters, wave energy devices, offshore installation and submerged damping devices for floating structures; the structure can be located quite close to the free surface and hence may undergo large/irregular amplitude motion. In these situations, numerical models based on assuming small amplitude motions, nonlinearity of either of the free surface or of the body dynamics, may not accurately represent the realistic dynamics of the coupled system. Based on this idea,the present study presents a fully nonlinear three dimensional model which can deal with near surface fully submerged structures.

In fact, the study of the submerged bodies in water waves was first started by Dean (1948) when he analyzed the interaction between gravity monochromatic waves and a fixed submerged horizontal circular cylinder using a linearized potential theory and the conformal mapping technique. In that study Dean showed that, to the first order there is no reflection of incident waves by the circular cylinder, and that transmitted waves only undergo a phase shift when passing the obstacle. Later, Ursell (1950)obtained the complete linear solution and reproduced Dean’s conclusions. Ogilvie (1963) and Mehlum (1980) had also confirmed and extended the work done by Dean (1948) on the diffraction problem. The work of Ursell (1950) and Ogilvie (1963) also investigated the wave radiation problem for a circular cylinder in forced oscillations and showed that it is possible to absorb all the power in a sinusoidal wave, by forcing a cylinder to move in a circular path.

Chaplin (1984) experimentally studied the influence of the Keulegan-Carpenter number on the nonlinear wave force applied to a fixed submerged cylinder. Since then, analysis of the hydrodynamic performances of submerged bodies has become increasingly important with the growing interest in offshore activities. Among those studies, more recently, Wu(1993) formulated a mathematical model to calculate the forces exerted on a submerged cylinder undergoing large-amplitude motions. Wu (1993) satisfied the no-flow boundary condition on the submerged body on its instantaneous position, while the free surface condition was linearized. Then Chaplin (2001), Schnberg and Chaplin(2003) performed more detailed experimental and numerical studies of the nonlinear wave interactions with a submerged horizontal cylinder. Following that, Kooet al.(2004)developed a two-dimensional fully nonlinear numerical wave flume based on the potential theory, MEL time marching scheme and boundary element method. This model was applied to determine wave characteristics and wave loads on submerged single and dual cylinders.

Among more recent studies, Condeet al. (2009)performed another experimental study in conjunction with the numerical analysis to study the fully nonlinear behavior of a two-dimensional horizontal cylinder in waves. After that, Guerberet al.(2012) extended a two-dimensional fully nonlinear potential wave model to include a submerged horizontal cylinder of the arbitrary cross-section. Other numerical tools for example, based on the Finite Element Method (FEM) were used to solve the Navier–Stokes equations by Tavassoli and Kim (2000, 2001) to analyze the interaction between nonlinear waves and a circular cylinder in a viscous two-dimensional numerical wave tank, and Baiet al. (2010) has studied the two-dimensional submerged dikes interaction with viscous free surface waves using the Cartesian cut cell approach.

The present study focuses on obtaining good insight into this classical problem by using a 3D fully nonlinear potential flow model based on the Boundary Element Method (BEM), which is an extension of the program developed by Bai and Eatock Taylor (2006, 2007, 2009) for simulating the wave radiation, wave generation, propagation and interaction with structures. The original code was modified to make it capable of considering fully submerged bodies either fixed or subjected to forced motions under wave actions. The overall approach is as follows. First the brief mathematical formulation is presented in Section 2,followed by its numerical implementation in Section 3. After that, Section 4 provides an analysis of the present numerical model’s accuracy based on the comparison with the published numerical results. In Section 5 the numerical results are given for a fully submerged vertical cylinder subjected to various forced sinusoidal motions and finally some concluding remarks are made in Section 6.

2 Mathematical formulation

To demonstrate the three-dimensional wave radiation problem, two right handed Cartesian coordinate systems are defined (Fig. 1). One is a space fixed coordinate system Oxyzhaving the Oxyplane on the mean free surface and the origin O usually at the center of the numerical tank. In this case thezaxis is positive upwards. The other is a body fixed coordinate system O′x′y′z′ with its origin O′ placed at the center of the mass of the body. When the body is at an upright position, these two sets of coordinate systems are parallel and the center of mass is located atXg= (xg,yg,zg)in the space fixed coordinate system. In Fig. 1,nis the normal unit vector pointing out of the fluid domain,SF,SDandSBrepresent the free surface, horizontal bottom and body surface, respectively.

Fig. 1 Sketch of the problem definition

2.1 Governing equations and boundary conditions

Based on the potential flow theory, the wave-body interaction problem can be formulated in terms of a velocity potentialφ(x,y,z,t), which satisfies Laplace’s equation within the fluid domainΩ,

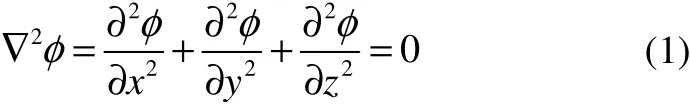
and is also subject to various boundary conditions on all surfaces of the fluid domain.

On the instantaneous free water surface, the following kinematic and dynamic conditions need to be satisfied,which are nonlinear, for the source of the difficulties associated with the water wave problem.

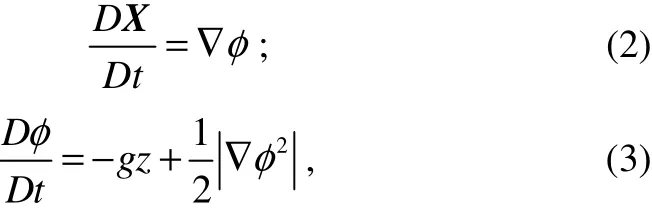
Here,D/Dtis the usual material derivative,Xdenotes the position of the points on the free surface, andgis the acceleration due to gravity.

The kinematic condition on the instantaneous wetted body surfaceSBis:

where,Vnis the velocity of the body in the normal direction.If small angular motions are assumed, the motions of a three-dimensional rigid body about its centre of mass can be described in terms of six components,

whereξ= (ξx, ξy, ξz) is a translatory vector denoting the displacements of surge, sway and heave andα= (αx, αy, αz)is a rotational vector indicating the angles of the roll, pitch and yaw respectively, about the Oxyzand measured in the counterclockwise direction. However, if a rigid body is considered, the boundary condition on the body surfaceSBwill become the same as that on the side wallSwand the horizontal seabedSD, which is known as the impermeability condition:

Here the body starts from rest in calm water, therefore the velocity potential and wave elevation can be used as the initial conditions and can be set to:

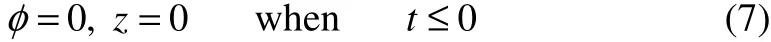
2.2 Higher order boundary element formulation

In this paper, the higher-order boundary element method is used to solve the mixed boundary value problem at each time step. In this numerical approach, the surface over which the integral is performed is discretised by quadratic isoparametric elements. For cases in which the body and the simulated flow are symmetric about thex–zplane, and the seabed is horizontal, the simple Rankine source and its images with respect to the symmetry plane and the seabed can be chosen as the Green’s function. Thus, the integral only needs to be evaluated over half of the computational boundaries, and the seabed is excluded. After assembling the equation for each node on the whole integral surface, a set of linear algebraic equations are obtained (for details see Bai and Eatock Taylor, 2006). Now, at a certain time step, either the potential or its normal derivative on each part of the boundary is known from the corresponding boundary conditions. Thus, the resulting set of linear algebraic equations can be solved to get the solution to the mixed boundary value problem (i.e. to find the remaining unknowns) at that certain time step.

2.3 Hydrodynamic forces

Once the potential has been found by solving the mixed boundary value problem at each time step, the pressure on the body is expressible using the Bernoulli equation. The hydrodynamic forcesF= {f1,f2,f3} and momentsM= {f4,f5,f6} on the body can consequently be obtained by integrating the pressure over the wetted body surface,

In the above equation, the main difficulty is the evaluation of the time derivative of the potential,φt. Estimating this quantity by a simple backward difference scheme is inaccurate and prone to instabilities in cases when a surface piercing body is free to move. For the fully submerged body considered here, such problems may not appear as the meshes on the body surface are unchanged. However, the present study will be extended to include the fully submerged and surface piercing bodies together, hence for calculating the hydrodynamic force with an effective method applicable for both fully submerged and surface piercing bodies is applied here, with the purpose of solving a separate boundary value problem, as used by Wuet al. (2003).

In Wuet al. (2003), a general equation of force for the wave-structure interaction problem was developed. For the wave radiation problem considered in the present study, the general equation is further modified by removing the force components caused by the wave maker. The final simplified equation to calculate the hydrodynamic force can be expressed as:

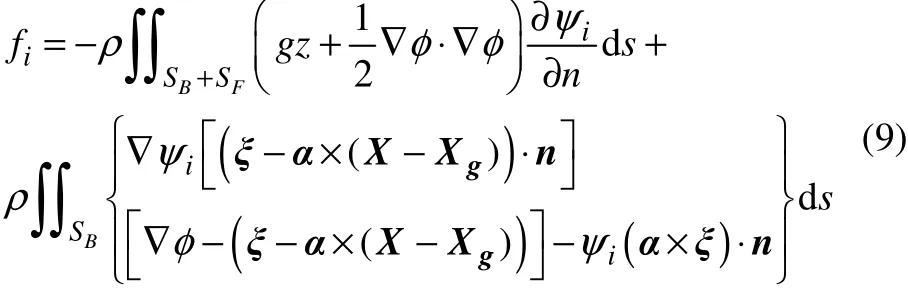
whereψis the auxiliary functions obtained by solving another boundary value problem.

3 Numerical implementation

The precision of the numerical simulation is dependent on the quality of the discretization used. Therefore, in the application of the numerical method to simulate nonlinear wave structure problems, a number of aspects related to the detailed performance have to be considered. For example,mesh generation on boundary surfaces, the time stepping integration technique to update the variables, algebraic equation solver to solve the matrix of the boundary value problem and the mesh refinement process to avoid instability represent the few important aspects of a numerical process which have a direct bearing on the success or failure of the calculations. The details of these methods can be found in Bai and Eatock Taylor (2006), only a brief summery is presented below.

In the present method, structured quadrilateral meshes are distributed on the vertical wall surfaces and the side surface of the body. On the free surface, the top and bottom of the truncated body, unstructured triangular meshes are generated by using the Delaunay triangulation method, which is well suited to fitting the complex computational domain. A double or triple node is employed for the intersections between the free surface and solid surfaces or the side surface and the top and bottom of the truncated body.

A circular numerical tank is simulated for the current study and in order to avoid the reflection of scattered waves from the tank boundary and to simulate a sufficiently long duration in a reasonably sized domain, an artificial damping layer on the free surface is adopted throughout the circular perimeter of the tank to absorb the scattered wave energy.Fig. 2 provides an illustrative outlook of the computational domain in order to create a visual impression of the tank.Fig. 2(a) depicts the sketch of the entire 3-D numerical wave tank with the vertical test cylinder inside the domain,whereas Fig. 2(b) shows the snapshot of the numerical grid used in the calculation for half of the computational domain(free surface and cylinder only) at a certain time step.

Fig. 2 Illustrative outlook of the computational domain

4 Fully submerged sphere in the heave motion

In this section, the wave radiation from a submerged heaving sphere in a circular cylindrical tank is simulated to test the ability of the present numerical model in simulating the nonlinear wave patterns and provide the resulting wave forces and other hydrodynamic parameters as well. Ferrant(1991) also studied this case, using a coupled time and frequency domain approach.

In his study, Ferrant used a submerged sphere with a mean depth of submergence equal to the sphere diameter and starting from the rest, the body was given a purely harmonic motion. Fig. 3 shows the comparison results for two different wave amplitudesa3/r= 0.5 and 0.7 associated with two values of the fundamental wave number (k1=ω2r/g)0.1 and 2.0. Here,a3, randωrepresent the sphere motion amplitude in the vertical direction, radius of the sphere and oscillation frequency respectively.

Fig. 3 Comparison of vertical forces in time for various combinations of k1 and a/r ratios

As can be seen, all four time plots agree quite well with the present results except for the initial differences, that have actually happened due to the application of a ramp function in the present analysis. Moreover, it is also noticeable that with the increase of the sphere radius or wave number, the wave forces found in the current study tend to increases as well. This phenomenon can be better visualized in Fig. 4. It seems that the increases happen due to the nonlinear effect of the free surface boundary conditions. With the increase of motion amplitudes and wave numbers, the nonlinearity is expected to become more prominent. However, in the analysis done by Ferrant, the body boundary conditions are applied at the actual time depending on the body surface and the free surface conditions being linearized. In contrast, the present analysis is fully nonlinear and seems to capture the higher harmonics quite well. Due to this reason, the findings of both studies are reasonably consistent for lower ranges of wave frequency and cylinder radius and deviate noticeably after that. The ability of the present numerical model in simulating nonlinear wave interactions with submerged structures near to the free surface is thus evident by this validation.

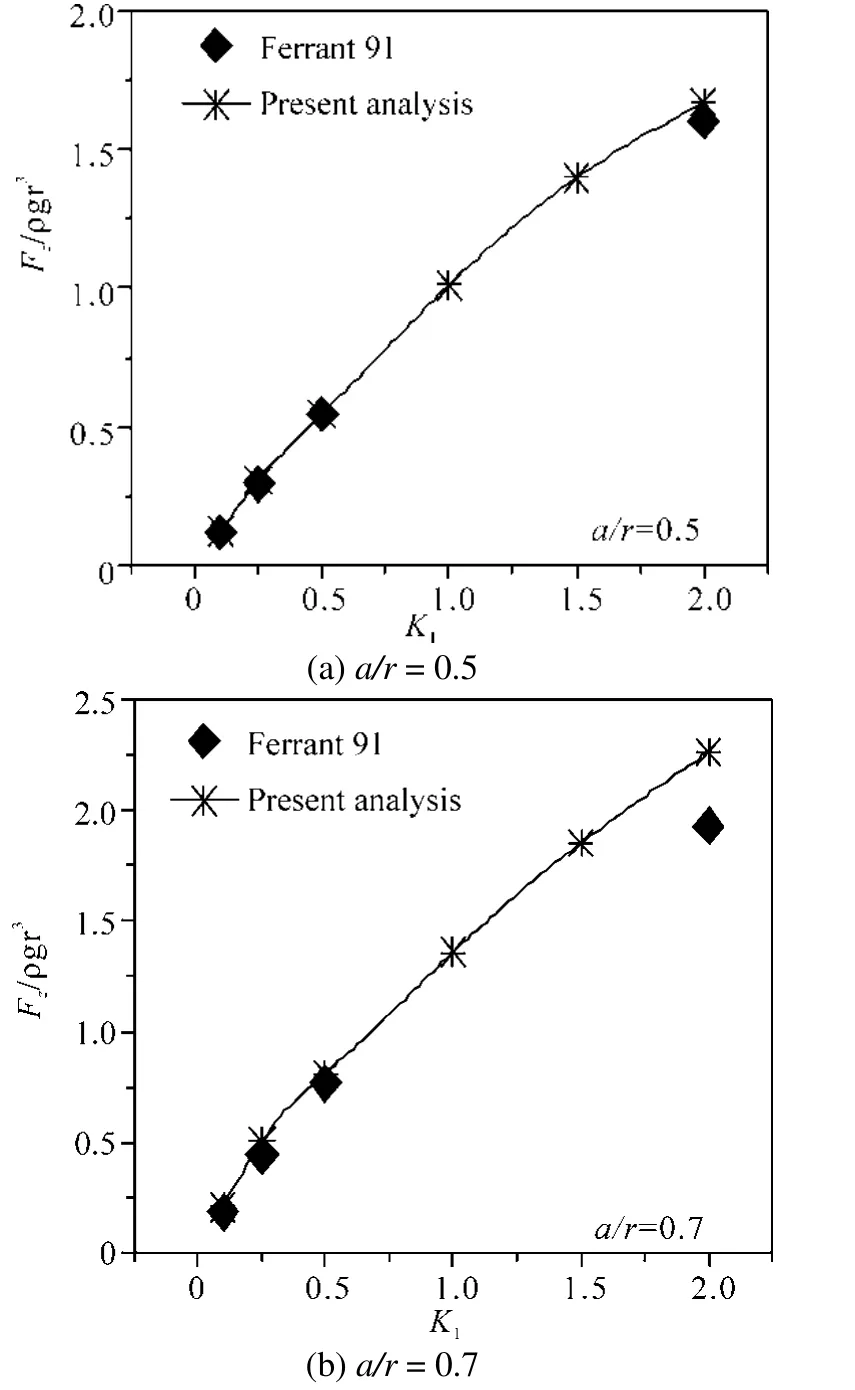
Fig. 4 Variation of heave forces with wave numbers:comparison of present results with Ferrant’s results for various a/r ratios

5 Wave radiation from a fully submerged vertical cylinder undergoing forced motion

In this section, nonlinear wave radiation from a fully submerged vertical cylinder undergoing several forced oscillatory motions is considered with various motion amplitudes and frequencies. It is important to note that the water depthd, gravitational accelerationgand fluid densityρare taken to be unified in all cases discussed onwards (unless otherwise specified), yielding results and time in the non-dimensional form. Other lengths are non-dimensionalised by the water depth. It should also be noted that the vertical hydrodynamic force presented in this paper is the total force obtained from Eq. (9) minus the mean hydrostatic force.

Throughout the parametric study of this section, a vertical cylinder with a lengthl =0.2dand with a radiusr =0.1d, is placed below the still water surface and set to sinusoidal motion about the centre point of the cylinder body. The cylinder is allowed to oscillate in a circular cylindrical tank having a radius given asR =2.5d, which is sufficiently large,as the focus here is to analyze the wave profile/elevation and the hydrodynamic force on the moving cylinder. In order to prevent reflection, a damping layer is implemented throughout the perimeter of the cylindrical tank. Moreover,due to the symmetry of the computational domain, only half of it is considered in the computation. The cylinder starts oscillating from its rest position, and the displacement and velocity of its motion are respectively given as:

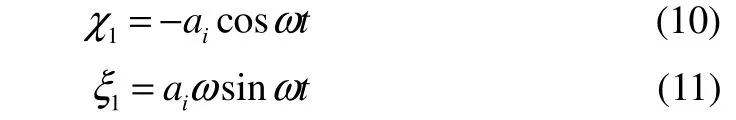
whereωis the oscillation frequency andaidefines the amplitude of the body motion. Also, throughout the study ‘t’represents the real time and ‘T’represents the wave period.

5.1 A fully submerged vertical cylinder with different motion amplitudes

This subsection provides an analysis of the effects of changes in motion amplitudes in cylinder responses for example, wave elevation, wave profiles and hydrodynamic forces. In order to carry out this study, a submerged cylinder is placed atD= 0.1dbelow the free surface and set to surge,heave and a combined surge-heave motion respectively at a constant oscillation frequency of ω = 2.0 with several motion amplitudes (a). The rest of the parameter is kept unchanged as mentioned at the beginning of section 5. It is important to indicate that during the combined motion the equal amplitude is used for both the surge and heave motions throughout the study of this paper (unless otherwise specified).

Among the three types of motion investigated; here Fig. 5 shows the wave profiles generated by the cylinder under various heave motion amplitudes, Fig. 6 represents the time history of wave elevation at certain points in different amplitudes of combined motion and Fig. 7 shows the time history of vertical dynamic forces due to the change of heave amplitudes.

Fig. 5 Wave profile at t = 9T for different heave motion amplitudes

Fig. 6 Changes in wave elevation at x = −0.1 for various combined motion amplitudes

Fig. 7 Variation in vertical dynamic wave forces due to changes in the heave motion amplitudes

These figures clearly reveal that the numerical results are very stable during the whole simulation period. As can be seen, no strong nonlinearity is noticed in the hydrodynamic forces, except for some slight fluctuation near the crests which appear with the increase of amplitudes. However, the changes in wave profiles and wave elevations are quite noticeable especially at higher amplitudes. The wave profile becomes very complex as the amplitude rises and the high harmonics occur which clearly indicate the presence of high nonlinearity.

Fig. 8 Changes in the maximum forces and elevation due to the variation of cylinder motion amplitudes

In Fig. 8, a summary of the influences of various motion amplitudes over hydrodynamic forces and wave elevation for surge, heave and combined motion are presented. Here the maximum values of wave forces and wave elevations(obtained after the steady state is reached) are plotted against the normalized amplitudes. The horizontal dynamic force of the combined motion are plotted with a pure surge motion output and the vertical dynamic force of the combined motion are plotted with a pure heave motion output for better comparison purposes. As noticed in Fig.8(a), nonlinearity in horizontal dynamic force for pure surge motion is not very strong, whereas in case of combined motion it is quite visible and seems to appear due to heave component of motion. Although based on linear theory,heave motion not supposed to contribute towards the horizontal force components. However, influence of heave here is quite significant which might be occurring either because of the nonlinearity present in heave motion or because of the nonlinear interactions between surge and heave during combined motion. Rest of the two plots, Fig.8(b-c) show the variation in maximum vertical dynamic force and wave elevation respectively, with the increase of motion amplitude. As observed, the nonlinear influence of heave and combined motion is quite prominent in these responses and both the parameters seem to vary rather similarly with the change of amplitude for heave and combined motion. That means during combined motion heave seems to dominate over the surge part. In fact, from all three plots of Fig. 8 it appears that only the heave and combined motions generate strong nonlinearity and the nonlinearity in combined motion is mostly controlled by the heave portion.

5.2 A fully submerged vertical cylinder with different oscillation frequencies

Having considered the variation of the motion amplitudes,the impact of change of the oscillation frequencies on the surge, heave and combined motions of the submerged cylinder is now studied in this subsection. For all the analysis presented here, the motion amplitude of the cylinder is kept constant at 0.02 and the cylinder is placed atD= 0.1dbelow the free surface.

At first, the effects of the frequency changes on the heave motion of the cylinder is investigated and Figs. 9, 10 and 11 show the results as the time histories of the wave elevation,wave profiles and hydrodynamic forces respectively; for three different oscillation frequencies.

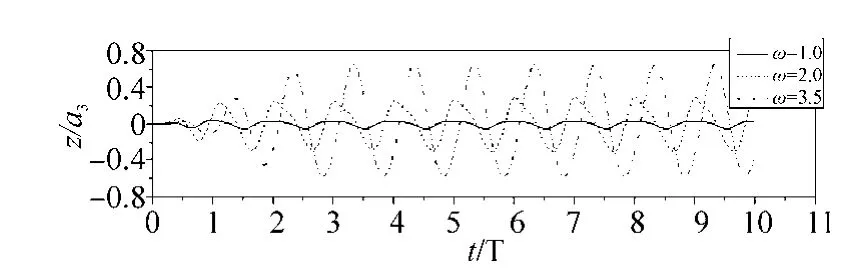
Fig. 9 Wave elevation histories at x ≈−0.1 for various frequencies in the heave motion, a3=0.02

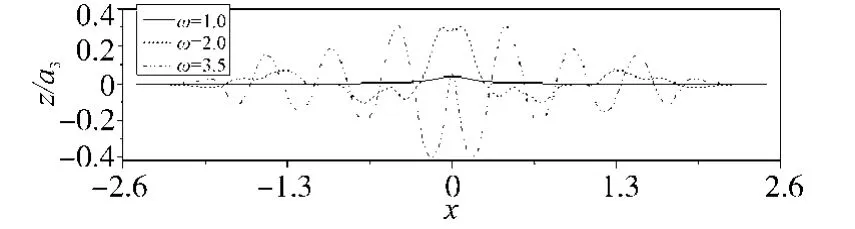
Fig. 10 Wave profiles at t= 9.0T for the oscillating cylinder with different frequencies, heave motion a3=0.02

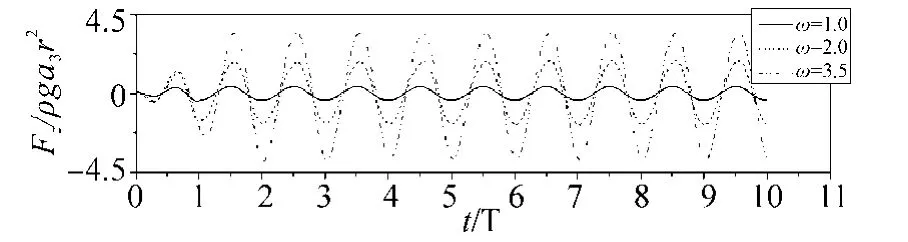
Fig. 11 Vertical hydrodynamic forces on the cylinder due to changes of frequency, heave motion a3=0.02

As observed from these figures, the phase of wave elevation and wave forces gradually shift from the phase of cylinder motion with the increase of the oscillating frequencies, although the shifting of wave forces is less pronounced. It is also noticed that the normalized amplitude of the wave elevations and wave forces increase abruptly with the increase of frequencies, which in turn reveals the effects of nonlinearities.

Similar investigations as above have been carried out for surge and combined heave-surge motions of the submerged cylinder as well. However, in Figs. 12-14, only a FFT (Fast Fourier Transform) analysis of the hydrodynamic forces and wave elevation (at a certain point) is presented in order to realise the overall impact of frequency changes in surge,heave and combined motions of the cylinder. The components of the dynamic horizontal force and vertical force on the cylinder are plotted in Fig. 12 and Fig. 13,respectively. Whereas, the FFT analysis of wave elevation is depicted in Fig. 14.

As expected and as can be seen from Fig. 12(a) and Fig.13(a), both the 1stharmonic of the horizontal and vertical forces increase significantly with the increase of frequency.However, it is interesting to observe that the combined motion does not produce any noticeable change in the 1stharmonic. Though, its contribution to nonlinear components is quite visible, particularly in the case of the horizontal force. Comparing Fig. 12(b-c), it is evident that the 2ndand 3rdorder components from the combined motion are significantly higher than that from the surge motion. On the other hand, Fig. 13(b-c) shows that the 2ndorder contributions are quite similar for both the heave and combined motions. And although the 3rdand 4thorder seems to have a similar pattern, the components from the combined motion tends to be a bit larger compared to the pure heave motion. In short, it can be concluded that, although it looks like the combined motions do not produce any significant effects (as long as the linear aspects are considered), this combined surge-heave motion produce remarkable contributions toward the nonlinear responses which might be of interest in some practical cases.

Fig. 12 Change in maximum horizontal dynamic wave forces with frequency: (a) 1st harmonic for surge and combined motion;(b) 2nd and 3rd harmonics for surge motion; (c) 2nd, 3rd and 4th harmonics for combined motions

Fig. 13 Change in maximum vertical dynamic wave forces with frequency: (a) 1st harmonic for heave and combined motions;(b) 2nd and 3rd harmonics for heave motion; (c) 2nd, 3rd and 4th harmonics for combined motions

Fig. 14 provides the FFT analysis of wave elevations at a certain point (x= −0.1) up to the 3rdharmonic. As can be seen, the first harmonic of the combined motion is dominated by the surge response. However in the case of the 2ndharmonic it appears that all three types of motion create similar responses at lower and higher frequencies, whereas they are dispersed significantly at midrange frequencies. At the higher harmonic (3rd) it seems that the heave response dominates the output of the combined motion and the components of the surge show a somewhat steady pattern regardless of the changes of frequency. This seems reasonable as the heave is supposed to produce greater nonlinearity as compared to the surge motion.

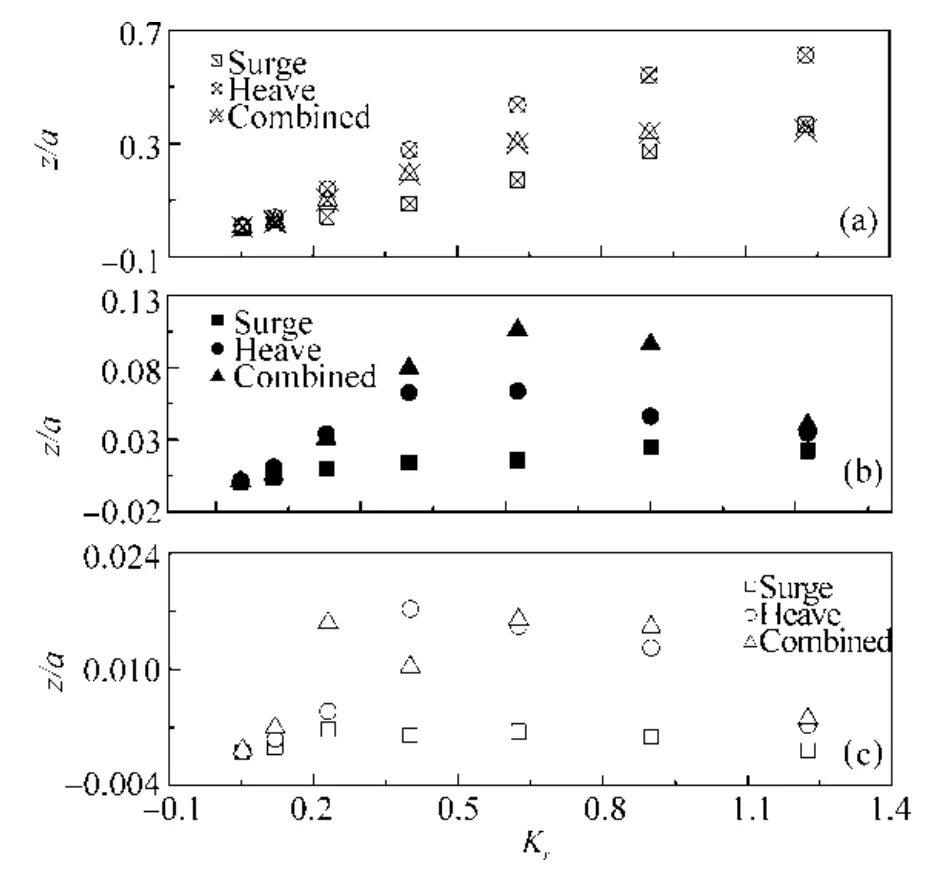
Fig. 14 Change of maximum wave elevation with frequencyat x=−0.1: (a) 1st harmonic; (b) 2nd harmonic; (c) 3rd harmonic

5.3 A fully submerged vertical cylinder subjected to combined heave and pitch motions

This final subsection analyzes the combined effects of the heave and pitch motions on hydrodynamic forces and wave responses created by the cylinder. In order to do so, few cases are designed to have a combined heave and pitch motion of the cylinder. However, the main objective here is to investigate the importance of the pitch motion in terms of producing nonlinear effects. Hence, in all of the cases the heave motion amplitude is kept constant (a3= 0.01) and the pitch motion angle (a5) is varied over a range of ‘0’ to π/20.It should be noted that for the analysis of this subsection the submerged cylinder is placed atD= 0.15dbelow the free surface and is allowed to have a forced sinusoidal pitch motion about a point 0.3dabove the free surface. Also the wave frequency is kept constant atω= 2.0 for all cases.

Fig. 15 and Fig. 16 show the resultant time history of the vertical and horizontal dynamic force respectively on the cylinder for four pitch angles. It is evident from Fig. 15 that the vertical dynamic force starts to gain a non-zero positive mean with increasing pitching amplitudes and the level of nonlinearity also becomes stronger at the same time. In contrast the horizontal force depicted in Fig. 16, although near to zero without the pitch motion, seems to increase consistently with the rise of the pitch angle. The complexities of wave profiles also seem to increase as more ripples appear at higher amplitudes (Fig. 17). These ripples indicate that some higher-order nonlinear components induced by the larger pitch amplitude are superimposed on the basic linear solution obtained at the smaller pitch amplitude. The time history of the wave elevation (Fig. 18)also confirms the presence of a considerable amount of nonlinearities. The elevation history starts to gain a strong negative mean value with the increase of the angular motion and thus creates a comparatively sharper trough. In brief, it can be concluded that compared to the linear combined motion, the rise of the angular pitch motion amplitude introduces significant nonlinear behaviour in the hydrodynamic responses produced by the submerged structure especially in the vertical hydrodynamic force,wave profile and wave elevation.

Fig. 15 Comparison of vertical dynamic forces for various pitch motion amplitudes (ω=2.0, heave amplitude, a3=0.01)

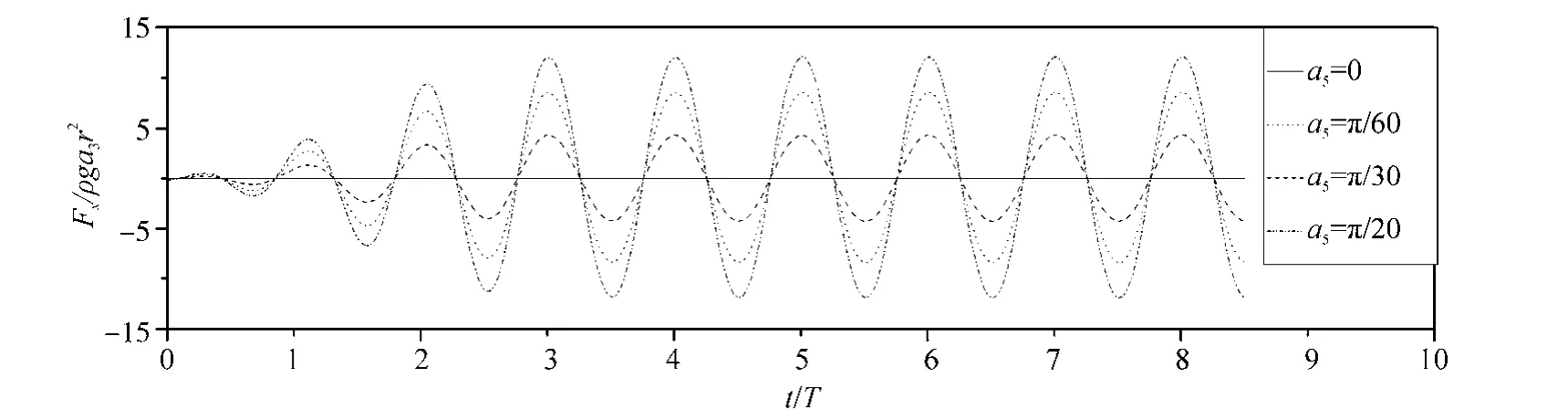
Fig. 16 Comparison of horizontal dynamic forces for various pitch motion amplitudes (ω=2.0, heave amplitude, a3=0.01)

Fig. 17 Wave profile behavior at t=9T with several pitch motions (ω=2.0, heave amplitude, a3=0.01)

Fig. 18 Variation of wave elevation at x= −0.1 for different pitch amplitudes (ω=2.0, heave amplitude, a3=0.01)

6 Conclusion

A three-dimensional fully nonlinear numerical wave model is presented to simulate the wave interaction with fully submerged structures subjected to forced sinusoidal motions. For the purpose of validation, at first, wave radiation from a fully submerged sphere is simulated using the present numerical model and comparisons are made with other numerical results. Strong agreement between the two findings demonstrates the capability of the present model for solving highly nonlinear, near surface problems.

After this is completed, the wave radiation from a fully submerged vertical truncated cylinder undergoing forced heave, surge and combined heave-surge motions is analysed and a brief parametric study is performed to determine the effects of the motion amplitudes and frequencies over the hydrodynamic parameters of interest. With the increase of the amplitudes, the combined motion significantly affects both the vertical and horizontal hydrodynamic forces.However, the wave elevation seems to be dominated by the heave motions as the combined elevations are almost similar to that of the pure heave elevation. The combined motion also creates noticeable nonlinearities with the increase of the motion frequency. Finally, the influence of the pitch motion on creating nonlinear behaviour was investigated and it was found that the increase of the angular amplitude can cause significant nonlinear effects toward the global response of the cylinder during a combined motion.

Bai W, Mingham CG, Causon DM, Qian L (2010). Finite volume simulation of viscous free surface waves using the Cartesian cut cell approach.International Journal for Numerical Methods in Fluids, 63(1), 69-95.

Bai W, Eatock Taylor R (2006). Higher-order boundary element simulation of fully nonlinear wave radiation by oscillating vertical cylinders.Applied Ocean Research, 28(4), 247-265.

Bai W, Eatock Taylor R (2007). Numerical simulation of fully nonlinear regular and focused wave diffraction around a vertical cylinder using domain decomposition.Applied Ocean Research,29(1-2), 55-71.

Bai W, Eatock Taylor R (2009). Fully nonlinear simulation of wave interaction with fixed and floating flared structures.Ocean Engineering, 36(3-4), 223-236.

Chaplin JR (1984). Nonlinear forces on a horizontal cylinder beneath waves.Journal of Fluid Mechanics, 147, 449-64.

Chaplin JR (2001). Nonlinear wave interactions with a submerged horizontal cylinder.11th International Offshore and Polar Engineering Conference, Stavanger, 272-279.

Conde JMP, Didier E, Lope MFP, Gato LMC (2009). Nonlinear wave diffraction by submerged horizontal circular cylinder.

International Journal of Offshore and Polar Engineering, 19,198-205.

Dean WR (1948). On the reflection of surface waves from a submerged, circular cylinder.Proc. Cambridge Phil. Soc.,483-491.

Ferrant P (1991). A coupled time and frequency approach for nonlinear wave radiation.Eighteenth Symposium on Naval Hydrodynamics, 67-83.

Guerber E, Benoit M, Grilli ST, Buvat C (2012). A fully nonlinear implicit model for wave interactions with submergedstructures in forced or free motion.EngineeringAnalysis with Boundary Elements, 36, 1151-1163.

Koo W, Kim MH, Tavassoli A (2004). Fully nonlinear wave-body interactions with fully submerged dual cylinders.International Journal of Offshore and Polar Engineering, 14, 210-217.

Mehlum E (1980). A circular cylinder in water waves.Applied Ocean Research, 2, 71-177.

Ogilvie TF (1963). First- and second-order forces on a cylinder submerged under a free surface.Journal of Fluid Mechanics, 16,451-472.

Schnberg T, Chaplin JR (2003). Computation of nonlinear wave reflections and transmissions from submerged horizontal cylinder.International Journal of Offshore and Polar Engineering, 13,29-37.

Tavassoli A, Kim MH (2000). Two-dimensional viscous-flow simulations for a circular cylinder in motion.10th International Offshore and Polar Engineering Conference, Seattle, 478-485.

Tavassoli A, Kim MH (2001). Interactions of fully nonlinear waves with submerged bodies by a 2D viscous NWT.11th International Offshore and Polar Engineering Conference, Stavanger, 348-354.

Ursell F (1950). Surface waves on deep water in the presence of a submerged circular cylinder.Proc. Cambridge Phil. Soc.,141-158.

Wu GX (1993). Hydrodynamic forces on a submerged circular cylinder undergoing large-amplitude motion.Journal of Fluid Mechanics, 254, 41-58.

Wu GX, Eatock Taylor R (2003). The coupled finite element and boundary element analysis of nonlinear interactions between waves and bodies.Ocean Engineering, 30, 387-400.