长大山岭隧道涌水量的BP神经网络时间序列预测模型
2014-07-30漆泰岳滕振楠
雷 波,漆泰岳,王 睿,李 延,滕振楠
(西南交通大学交通隧道工程教育部重点实验室,四川成都 610031)
我国西部长大山岭隧道工程穿越各种特殊、复杂的地层,处于不同应力场、渗流场和温度场环境中,面临各种各样的地质灾害[1]。其中隧道突涌水是长大山岭隧道施工过程中较为常见也是危害性很大的灾害,甚至会不同程度地影响隧道建成后的正常运营,引起地下水位下降、植被破坏以及地表沉降等生态环境问题,产生不良的社会影响。
国内外许多隧道施工中发生过涌水甚至突泥灾害,如法国仙尼斯峰隧道、日本青函隧道、前苏联北穆隧道、我国的衡广复线大瑶山隧道、大秦线军都山隧道、渝怀铁路圆梁山隧道和宜万铁路马鹿箐隧道、野山关隧道及大支坪隧道等,引起巨大工程损失和人员伤亡。因此在长大山岭隧道施工过程中,如何有效预测隧道涌水量一直是隧道防灾技术研究的重点问题而备受工程界关注。
1 隧道涌水量预测
目前常用的隧道涌水量预测计算方法有水均衡法、水文地质比拟法、解析法、数值法等。然而山岭地区的地下水的赋存条件复杂、运移方式多样,同时大气降水具有时空变异性,地表径流水量与地下水补给关系不确定,因此涌水量影响因素间的关系错综复杂,各因素对隧道涌水的影响具有模糊性。此外,地下水运动理论还不成熟、现有的勘探方法还不足以准确查明隧道涌水水源和通道分布、已有涌水量计算模型还不能真实地反映隧道涌水的复杂运动特征。这些因素使得上述传统方法存在局限性。其中理论公式经过严格的数学推导得出,其适用条件苛刻,在实际工程中应用性不广;数值计算方法应用比较广泛,适用性强,但对试验条件要求较高,计算成本大。
鉴于隧道涌水的高度非线性以及影响因素的不确定性,采用先前的公式法预测涌水量这种定量评价方法精度差,无法满足工程实际的需求。而采用BP神经网络时间序列模型,不需要考虑上述涌水量预测的影响因素的复杂性,可以实现一定精度的长大山岭隧道涌水量预测。
2 BP神经网络时间序列预测模型
近年来,BP神经网络时间序列模型发展成为数据预测的有效方法,具有较高的精度和稳定性。其研究与应用十分活跃。刘莉等[2]应用时间序列典型分解法提取原降水量序列中的趋势成分,建立降水量的BP神经网络时间序列预测模型,并在宿迁市进行了具体的应用。宋宇辰等[3]运用BP神经网络法和时间序列法,对包头市的二氧化硫、二氧化氮和可吸入颗粒物的年份浓度值和月份浓度值进行了预测。王卓等[4]对1980—1998年的铁路客运量进行归一化处理,建立铁路客运量时间序列神经网络预测模型,设计网络参数,进行网络学习与训练的仿真试验。
2.1 时间序列
时间序列分析(time series analysis)是根据动态数据揭示系统动态结构和规律的统计方法。其基本思想是根据系统有限长度的运行记录,建立能够比较精确地反映时间序列中所包含的动态依存关系的数学模型,对系统的未来行为进行预测[5]。
2.2 BP神经网络理论
BP算法中的学习过程由信号的正向传播计算误差与误差的反向传播修正两个过程来实现。这种信号正向传播与误差反向传播的权值调整过程就是学习训练的过程。该过程周而复始进行,一直延续到误差达到要求精度或者预先设定的学习次数为止[6]。
BP神经网络时间序列模型绝大多数采用了三层结构:输入层、一个隐层和输出层。Robert Hecht-Nielson(1989)证明了对于任意闭合区间连续函数都可以用含有一个隐层的BP网络来逼近[7]。因而用三层的BP网络来预测长大山岭隧道涌水量可以满足网络的精度要求。三层BP神经网络时间序列预测模型结构如图1所示。

图1 三层BP神经网络时间序列预测模型
2.3 BP算法的改进
虽然BP算法有着良好的数学基础,无论是其网络理论还是网络性能方面都趋于成熟,并且其强大的非线性映射能力得到了广泛的应用,但是仍然存在着学习收敛速度慢、易出现局部最小而达不到全局最优以及训练时新旧样本不连续等缺点。因此国内外为改进其性能进行了大量研究,并提出了许多方法,其中有代表性的是增加动量项和自适应调节学习率两种方法,有关具体内容参见文献[8]。
3 应用实例
3.1 工程概况
位于我国西南地区的某隧道全长2 335 m,最大埋深约为280 m。隧道穿越区域为云贵高原中山区溶蚀峰丛与洼地相间地带。当地气候潮湿多雨,年平均降雨量约为1 200~1 500 mm。隧道进口段及中部地段岩溶发育强烈,地表溶沟、溶槽、溶洞、竖井、漏斗、溶蚀洼地及地下暗河通道等岩溶形态沿岩层走向呈串珠状展布。地下水以岩溶水和基岩裂隙水为主,主要接受大气降水及地表径流补给,水量充沛。隧道洞身段位于岩溶水季节变化带内。其中部下穿3个溶蚀洼地,有利于大气降水汇集并渗入补给地下水。地下水的流动形成了与地表3个溶蚀洼地相对应的3个地下富水区,地下水量丰富。隧道施工过程中多次发生突涌水灾害,严重影响隧道施工。
3.2 BP神经网络时间序列涌水量预测模型
本文利用1999年6月—2000年6月该隧道正洞涌水量时间序列资料,采用BP神经网络模型确定非线性时间序列数据之间的相关关系,从而进行隧道涌水量的预测。
3.2.1 隧道涌水量时间序列数据及数值处理
由于BP神经网络采用Sigmoid类转移函数,为了避免因净输入绝对值过大而出现神经元输出饱和,继而影响收敛速度,对隧道正洞涌水量时间序列Q=(Q1,Q2,…,Qt)作尺度变换,进行归一化处理。设序列中最大、最小涌水量分别为Qmax,Qmin,则归一化后序列的第i个量xi为
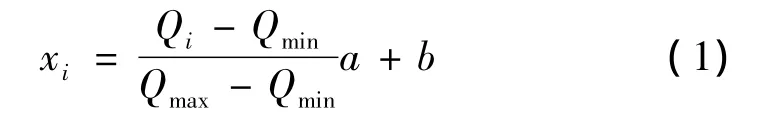
式中:a,b分别为参数,设 a=0.9,b=(1 -a)/2。
表1为该隧道正洞实测涌水量时间序列及其归一化处理结果。
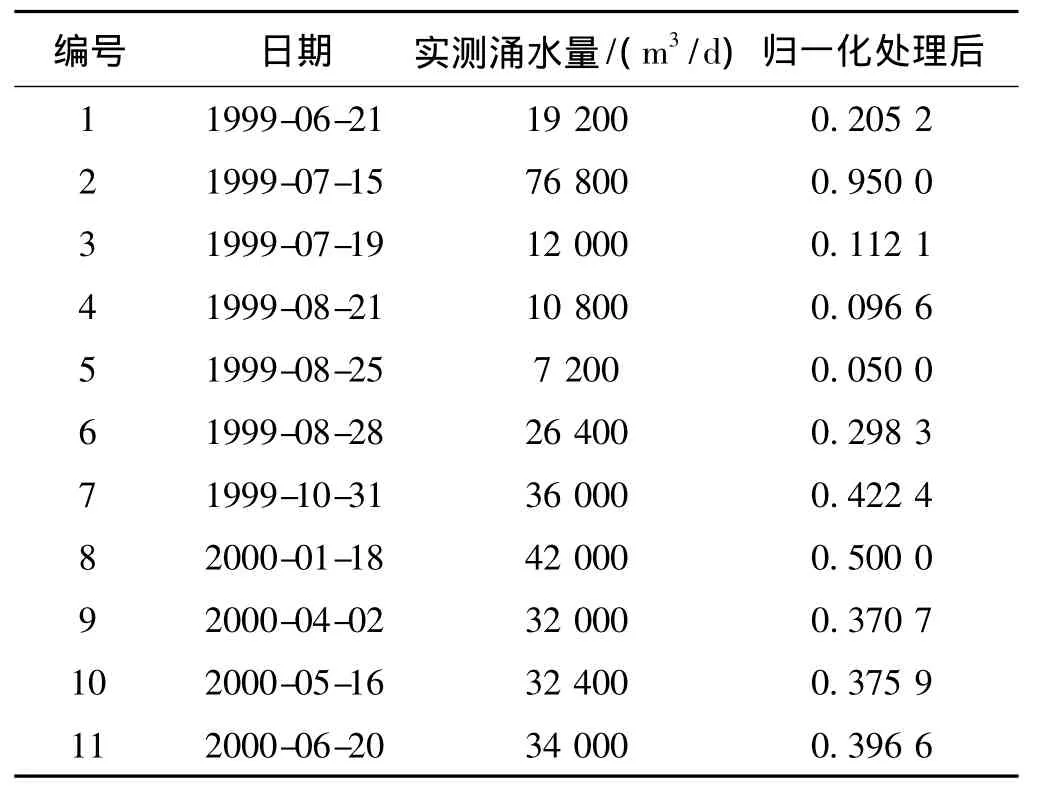
表1 隧道涌水量时间序列
3.2.2 BP网络结构参数设计及训练样本生成
采用3层神经网络以建立隧道涌水量预测模型,其中输入层节点数n=4,输出层节点数l=2,隐层节点数是神经网络模型至关重要的设计参数,极大地影响着模型预测性能。隐层节点数过少不足以体现训练样本的规律而忽略掉样本的重要信息;隐层节点数过多则容易将不具有规律性的噪声扩大化而出现“过度吻合”问题,从而降低模型泛化能力和收敛速度。确定最佳隐层节点数常用的一个方法为试凑法。隐层节点数初值先通过式(2)计算,然后逐渐增加隐层节点
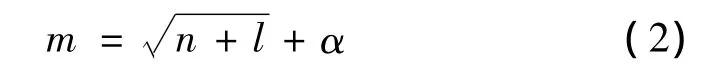
式中,α为1~10的常数。
计算时先取m=3,然后逐渐增加直到m=14并经过网络训练,根据试验结果可得本模型的隐层节点数m=12时,模型总误差最小,预测结果较好。数据经处理后的输入输出样本如表2所示。隐层神经元转移函数选用双曲正切S型传递函数,输出层神经元转移函数选用对数 Sigmoid函数,取允许最大误差为0.001,通过采用式(3)所示的自适应调整学习率的算法对BP神经网络进行算法改进。数,根据同一样本集训练的误差结果,选择最小误差对应的隐层节点数作为该模型的隐层节点数。

式中:η(t+1),η(t)表示前后两次迭代自适应调整学习率;E(t+1),E(t)为前后两次迭代误差。
3.3 预测结果及说明
应用MATLAB进行计算,经过127次训练后达到训练精度,隐层权重、输出层权重分别见表3、表4。将所要预测的样本 P8={0.500 0,0.370 7,0.375 9,0.396 6}输入网络中进行仿真计算,得到下一次预测结果为T预测=0.396 7,则隧道在施工过程中接下来要发生的一次涌水量预测值可由式(4)计算
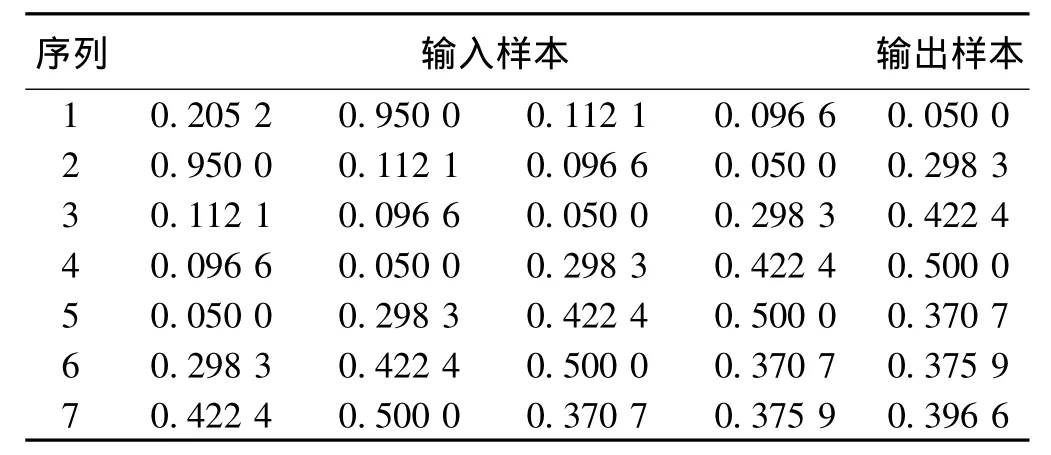
表2 神经网络训练样本
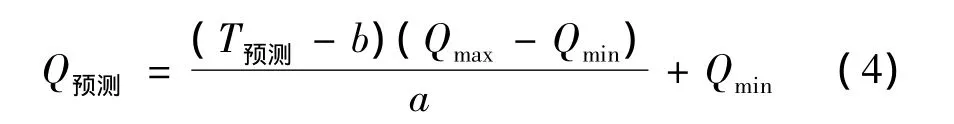
经计算得Q预测=33 934 m3/d。实际情况是,在随后紧接着的2000年6月26日发生大涌水,其中出口段正洞内3处涌水,实际总涌水量实测值 Q实际≈36 000 m3/d,可知BP神经网络模型预测误差约为5.74%,满足精度要求。

表3 隐层权重

表4 输出层权重
4 结论
1)长大山岭隧道高程远低于地下水位,水源充足,涌水量大,隧道穿越地区工程地质条件和水文地质条件变异性明显,涌水量影响因素多且各因素之间关系复杂,因此传统的涌水量预测方法存在局限性。应用BP神经网络时间序列预测模型的非线性特性,不必考虑隧道涌水量的影响因素及其间的关系,实例计算结果表明,该方法可以实现一定精度的涌水量预测。
2)BP神经网络时间序列隧道涌水量预测模型,其输入输出变量是依据隧道涌水量历史数据。在隧道施工期间由于缺乏初始涌水量数据,采用该方法预测较困难,必须应用超前地质预报方法进行探测。
[1]马士伟,梅志荣,张军伟.长大隧道突发性地质灾害预警信息系统研究[J].中国安全科学学报,2009,19(5):103-108.
[2]刘莉,叶文.基于BP神经网络时间序列模型的降水量预测[J].水资源与水工程学报,2010,21(5):156-159.
[3]宋宇辰,甄莎.BP神经网络和时间序列模型在包头市空气质量预测中的应用[J].干旱区资源与环境,2013,27(7):65-70.
[4]王卓,王艳辉,贾利民,等.改进的BP神经网络在铁路客运量时间序列预测中的应用[J].中国铁道科学,2005,26(2):127-131.
[5]王振龙.时间序列分析[M].北京:中国统计出版社,2000.
[6]韩立群.人工神经网络教程[M].北京:北京邮电大学出版社,2006.
[7]HSU K,GUPTA H V,SOROOSHIAN S.Artificial neural network modeling of the rainfall runoff process[J].Water Resources Research,1995,31(10):2517-2530.
[8]施彦,韩力群,廉小亲.神经网络设计方法与实例分析[M].北京:北京邮电大学出版社,2009.
