简支板桥在车辆荷载谱作用下的动力学分析

杨雅勋，赵殿英，黄 华

(1.长安大学 公路学院，陕西 西安 710064;2.河北兴诚交通科技有限公司，河北石家庄 050091;3.长安大学建筑工程学院，陕西西安 710064)

随着国民经济的不断发展，客运与货运的交通量显著增长，公路桥梁上行驶的车辆轴重不断加大，车辆密度逐渐提高，桥梁在车辆动荷载作用下的动态响应成为研究人员十分关心的问题。多年来，从古典的弹簧质点体系到现代车桥相互作用理论，人们对桥梁动力响应问题进行了大量研究[1-4]。然而这些工作大都局限于少量车辆通过桥梁时的情况，无法体现各型车辆随机出现时对桥梁的动力作用。本文基于结构动力学理论，利用自编程序VLS(Vehicle Load Spectrum)产生随机车辆荷载谱，通过有限元方法进行了简支空心板钢筋混凝土桥梁的动态响应分析。

1 随机车辆荷载谱

将设计基准期内桥梁构件所经历的实际运营荷载(或运营荷载与标准活荷载的比值)，按其大小及出现次数全面开列出来即为荷载谱，又称活荷载频值谱。由于桥梁通行的车流是一随机过程，车型、车重、车间距都随时间的变化而变化，国内外的统计数据表明[5]:车重、轴重、一般运行状态车间距、密集运行状态车间距服从对数正态分布;一般运行状态时间间隔、密集运行状态时间间隔服从伽马分布，车辆荷载概率分布类型及其参数见表1。

表1 车辆荷载概率分布类型及其参数

根据文献[5-6]，自编程序 VLS(Vehicle Load Spectrum)产生随机车辆荷载谱，其基本流程如图1。

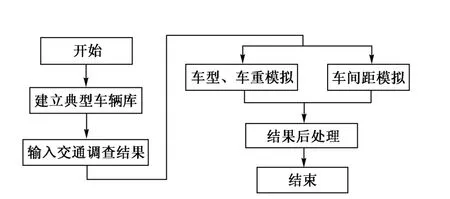
图1 随机车辆荷载谱模拟流程

程序以文献[6]提供的模型车辆为基础，建立了模型车辆库。依据文献[5]的统计数据，利用MATLAB程序的统计工具箱抽取随机数列，建立与交通调查结果的对应关系，实现随机车辆荷载谱模拟。依据文献[6]的交通调查结果，模拟上海市内环线中山路3号桥梁密集运行状态下的车辆荷载谱，如图2。

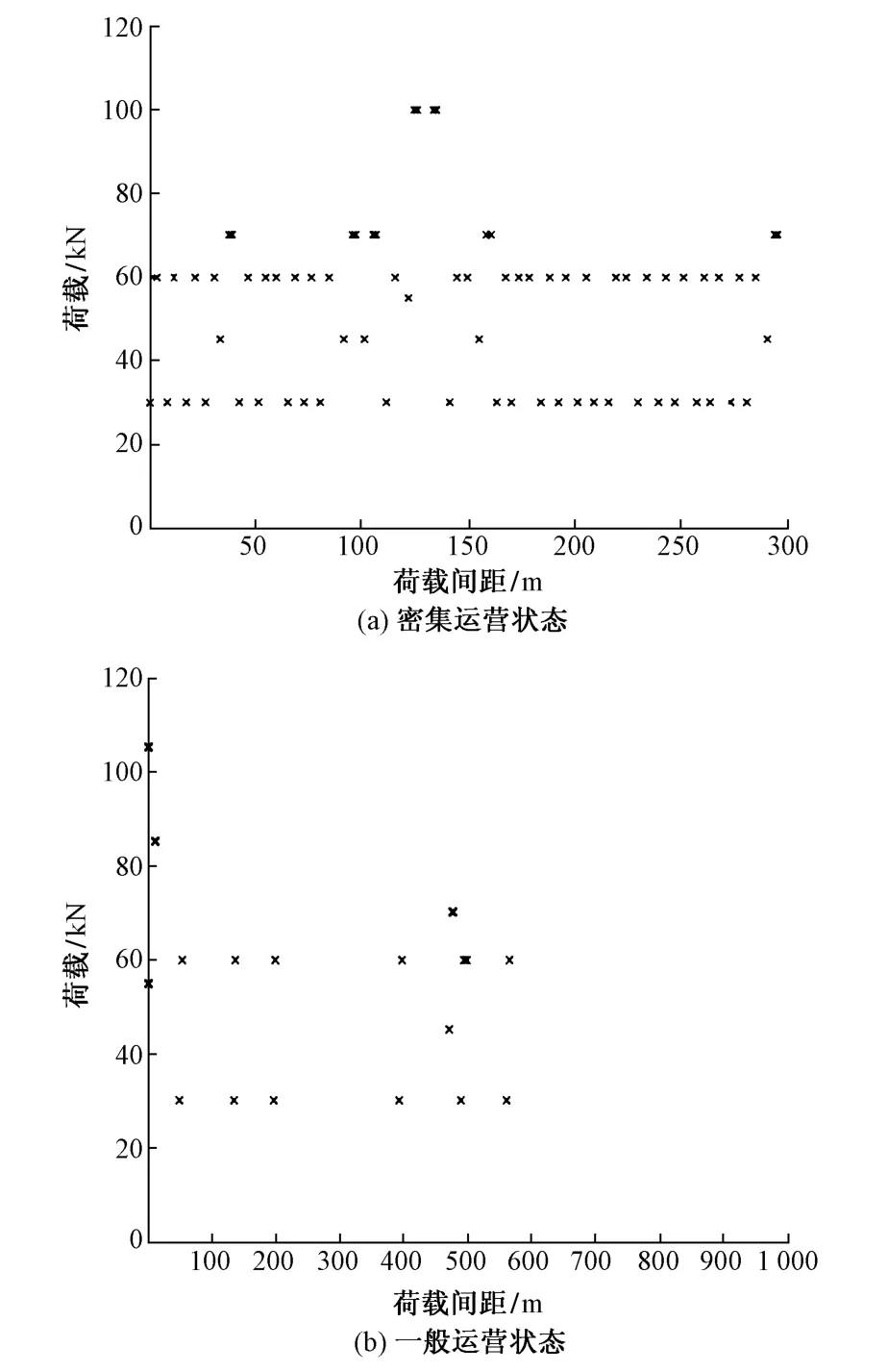
图2 桥梁车辆荷载谱模拟

2 有限元分析的动力学理论[7-8]

用有限元法分析结构振动以及动态响应问题与用有限元法分析结构静力学问题一样，把物体离散为有限个数的单元体，在考虑单元特性时，物体所受到的荷载还要考虑单元的惯性力和阻尼力等因素。

阻尼系数v与频率有关，通常采用雷利阻尼，令阻尼矩阵Ce=αMe+βKe，由单元刚度矩阵Ke，质量刚度矩阵Me及阻尼矩阵Ce组装成整体刚度矩阵K，质量刚度矩阵M及阻尼矩阵C，在不考虑体积力的情况下，整个结构系统的动力学方程为

当p(t)=0，C=0时得自由振动时的无阻尼动力学方程

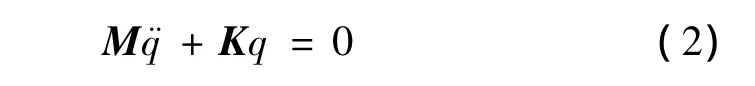
结构系统的动力响应，主要是解系统的动力方程式(1)，以求得系统产生的位移、速度、加速度的值。

3 简支板桥有限元动力学分析

3.1 有限元模型

简支空心板桥跨径15 m，桥面净宽5 m，人行道2×1 m，全跨由7块预应力空心板组成，具体尺寸如图3。桥面铺装荷载13.9 kN/m，人行道杆荷载单侧为8 kN/m，板与板之间通过铰缝连接，只传递剪力不传递弯矩。将桥面铺装、人行道杆、铰缝等重量分摊给7块板，得空心板的质量密度为3 541.4 kg/m3。由于只考虑桥梁在车辆荷载下的动力响应，而不分析其极限承载力、开裂、裂缝等情况，有限元模型采用solid45。网格划分采用六面体单元，共划分为48 807个单元、66 490个节点，如图4。

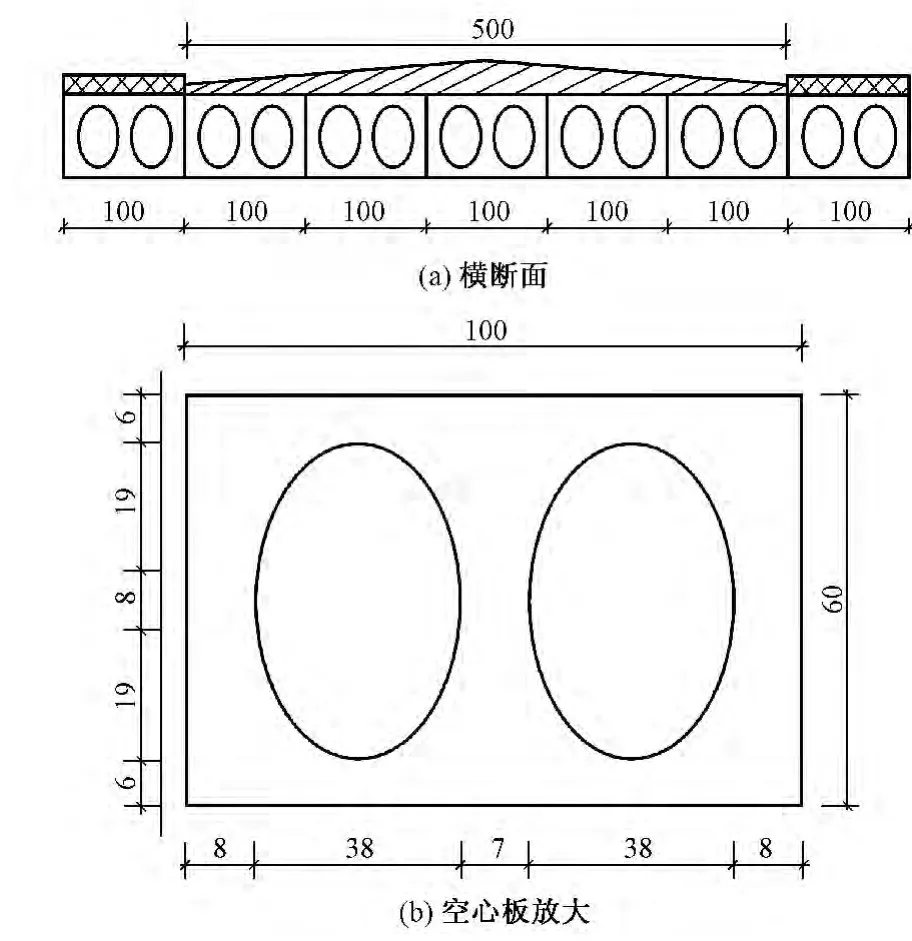
图3 简支空心板桥简图(单位:cm)

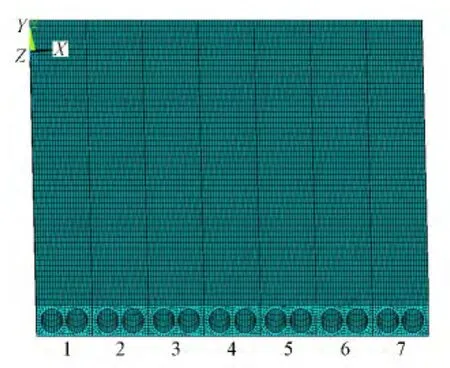
图4 空心板桥有限元模型

3.2 动力分析

有限元程序瞬态动力学分析有3种计算方法:完全法、模态叠加法和简化法。完全法采用完全的系统矩阵进行计算，不考虑选择自由度和模态形状，允许包含所有的非线性，求解精度高，故分析过程采用完全法。

计算荷载采用图2(a)所示密集运行状态下的随机车辆荷载谱，以10 m/s的速度通过桥梁，加载位置为沿图4的2，4号板面中轴线。人群荷载(3.5 kN/m2)作为恒载施加于1，7号板，且考虑重力荷载作用，计算得2号板底中轴线1/4跨、跨中、3/4跨(节点167，168，169)的位移时间历程曲线如图5，4号板底中轴线1/4跨、跨中、3/4 跨(节点 339，340，341)的位移时间历程曲线如图6，各板底中轴线跨中节点的位移时间历程曲线如图7。

图5 167，168，169节点位移时间历程曲线

由图5可见，车辆荷载作用下，桥梁最大位移不一定出现在节点168处。换言之，桥梁的最不利位置不一定出现在跨中节点处。这是由于车辆荷载作用位置、车辆间距的不确定性造成的。

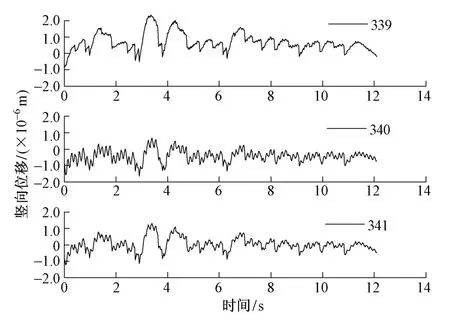
图6 339，340，341节点位移时间历程曲线

由图6可见:4号板在车辆荷载作用下出现了正向位移，且最大值出现在1/4跨节点339处，负向位移最大值出现在跨中节点340处，且在特定时刻节点339，340，341分别处于正负向位移状态。这反映了桥梁结构整体振型的复杂性。

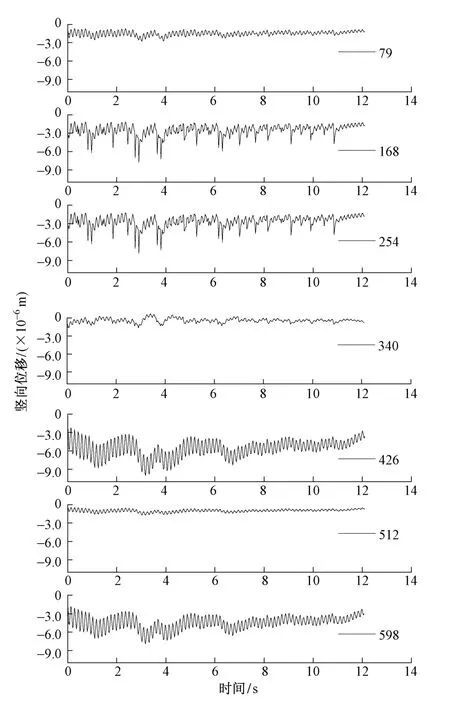
图7 各板底跨中节点的位移时间历程曲线

图7反映了1～7号板的跨中节点的振动情况。分析表明横桥向同样存在多种振型。

由图5至图7可见，车辆偏载情况严重，曲线形式与桥梁跨度、荷载间距、荷载值、车速等因素有关。图中最大位移为1×10－5m，所以小跨度桥梁车辆的振动作用对公路桥梁可以忽略，从而按静荷载处理。

节点168，340的加速度时间历程曲线见图8和图9。对比图8，图9可见，168节点的加速度比340节点大，偏载情况下边缘板块振动比中间板块强烈。这是由于边缘板块对中间板块的振动起到了一定的约束作用。

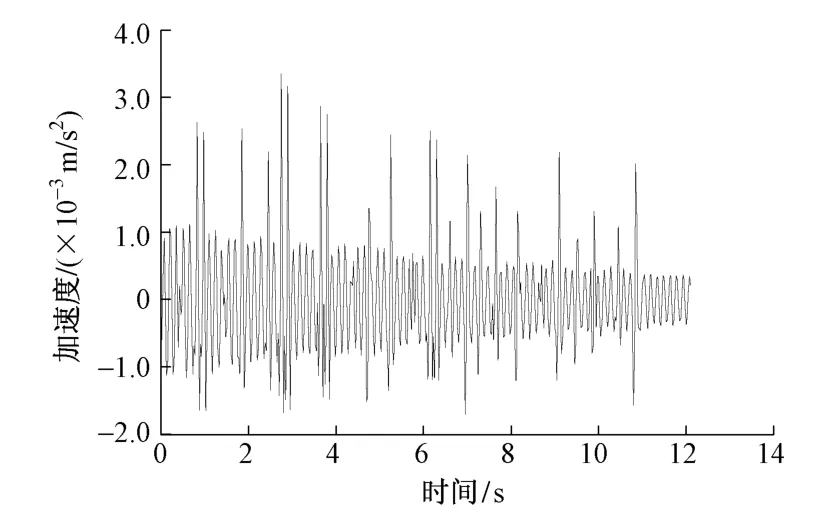
图8 168节点加速度时间历程曲线

图9 340节点加速度时间历程曲线

4 结论

本文利用自编程序产生随机车辆荷载谱，利用大型通用有限元程序将密集运行状态下的随机车辆荷载谱加载于简支空心板桥梁上，分析了车辆荷载对桥梁的动力响应，得出如下结论:

1)车辆荷载作用下，最大位移不完全发生在跨中节点处，危险点存在于跨中一段范围内。且不同板块振动情况差距较大，中间板块由于边缘板块的约束作用而振动较弱。桥梁整体振型复杂。

2)车辆荷载作用偏载情况严重，曲线形式与桥梁跨度、荷载间距、荷载值、车速等因素有关。

3)车辆荷载作用下桥梁最大位移很小(图中为1×10－5m)，小跨度桥梁车辆的振动作用对公路桥梁可以忽略，从而按静荷载处理。

[1]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社，1992.

[2]王贵春，章长玖，陈淮.公路简支梁桥在车桥耦合作用下的冲击系数研究[J].铁道建筑，2011(9):20-23.

[3]王元丰，许士杰.桥梁在车辆作用下空间动力响应的研究[J].中国公路学报，2000，13(4):37-41.

[4]单德山，李乔.荷载列作用下简支曲线梁的动力响应[J].重庆交通学院学报，2001，20(1):6-9.

[5]李扬海，鲍卫刚，郭修武，等.公路桥梁结构可靠度与概率极限状态设计[M].北京:人民交通出版社，1997.

[6]童乐为，沈祖炎，陈忠延.城市道路桥梁的疲劳荷载谱[J].土木工程学报，1997，30(5):20-27.

[7]龙驭球，包世华.结构力学[M].2版.北京:高等教育出版社，1994.

[8]R.克拉夫.结构动力学[M].王光远，译.北京:高等教育出版社，1979.