改进的HFEM公钥密码方案在数字签名上的应用设计

宋 严，赵永哲

(1.长春师范大学网络中心，吉林 长春 130032；2.吉林大学计算机科学与技术学院，吉林 长春 130012)

改进的HFEM公钥密码方案在数字签名上的应用设计

宋 严1，赵永哲2

(1.长春师范大学网络中心，吉林 长春 130032；2.吉林大学计算机科学与技术学院，吉林 长春 130012)

通过讨论HFEM公钥密码方案中解密的效率问题，提出了改进的HFEM公钥密码方案(I-HFEM).给出了I-HFEM方案的定义和算法，证明了I-HFEM方案的私钥尺寸以及解密开销都较原方案大为减少，并通过实例说明了I-HFEM方案在数字签名领域上应用的重要意义.

HFM公钥密码；HFEM；I-HFEM；签名方案；有限域上的遍历矩阵

HFEM公钥密码方案[1]在2009年申请了专利后，开始在数字签名领域使用.所谓HFEM，即隐藏有限域上遍历矩阵的公钥密码(Hidden Field Ergodic Matrices’ Public Key Cryptography)，它是基于有限域上BMQ问题的难解性以及遍历矩阵的特性所实现的一种新的公钥密码方案.所谓BMQ问题，是指有限域上的二等分多变元二次方程组求解问题(Bisectional Multivariate Quadratic Equations Solving Problem).该问题已经被证明是一个NP完全问题.但原始的HFEM方案存在私钥尺寸较大以及解密效率较低的缺点，因此，本文对其进行了改进，改进后的方案记为I-HFEM(Improved HFEM).与HFEM方案相比，I-HFEM不仅减小了私钥尺寸，还大大提高了解密的效率.

1 背景理论

1.1 HFM-PKC方案设计

所谓HFM-PKC，即“隐藏域上矩阵的公钥密码[2](Hidden Field Matrices’ Public Key Cryptography)”是基于有限域上BMQ问题的困难性以及有限域上矩阵的性质所实现的一种公钥密码.HFM-PKC的实现需要满足如下条件的矩阵集合A和B：

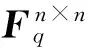
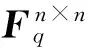
(3) |VS(A)VS(B){0}|=(qn-1)2/(q-1)；

(4) Rank(AB)=2n.

1.2HFEM的实现

HFEM公钥密码方案主要由密钥生成、加密、解密3个部分构成.

HFEM公钥密码方案密钥生成部分为其提供CA使用，为每个用户产生一对私钥和公钥，其实现方法如下：

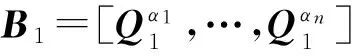
(5) 由RB生成2n个Fq上的BMQ多项式

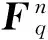
(6) 公钥为(Fq，ρ=[ρ1(x，y)，…，ρ2n(x，y)]，私钥为(B1M，B2，λ).

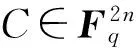
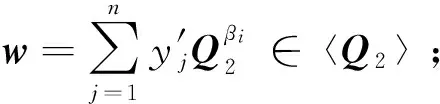
(4) 利用高斯消元法求出w的逆矩阵w-1∈〈Q2〉；

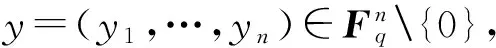
(6) 则(x，y)必与(α，β)等价，由此可还原出P=x⊗y=α⊗β.

由有限域上遍历矩阵的性质[3]可知(A=B1M，B=B2)满足条件(1)和(2).又由exp(Q1，M，Q2)=1和M∈R2(Q1，Q2)，可知(A，b)亦满足条件(3)和(4).这样的(A，B)数量众多，所以HFEM方案是可行的.

1.3HFEM效率分析

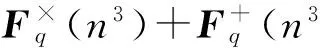
2 I-HFEM的设计与实现

2.1 I-HFEM的设计思想

由前面对HFEM解密算法的效率分析，不难发现其开销主要由解密算法第2步的开销决定.所以应将优化的重点放在如何才能减少解密算法第2步的开销.在原HFM-PKC方案的基础上，对约束条件进行了精炼，新的约束条件变为[5]：

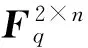
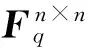
(3) |VS(A)VS(B){0}|=(qn-1)2/(q-1)；

(4) Rank(AB)=2n.

如果存在众多满足上述约束条件的(A，B)，则可实现改进的HFM-PKC方案.

密钥生成部分：

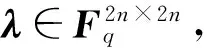
(3) 由RAB生成2n个Fq上的BMQ多项式ρk(x，y)=Rk[x⊗y](1≤k≤2n)；

(4) 公钥为(Fq，ρ=[ρ1(x，y)，…，ρ2n(x，y)]，私钥为(A，B，λ).

解密部分：

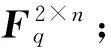
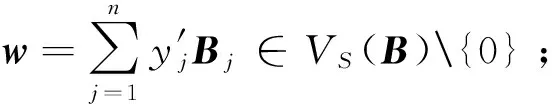
(4) 利用高斯消元法求出w的逆矩阵w-1∈VS(B){0}；

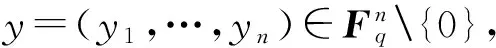
(6) 由(x，y)还原出明文P=x⊗y=α⊗β.

效率分析：

改进的HFM-PKC方案的私钥尺寸[6]为[(n3+6n2)log2q] B，比原来的(4n3log2q) B减少了将近3/4.更为重要的是，这使得解密算法的开销大大降低.下面对其详细分析：

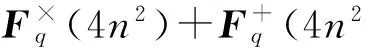
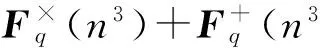
2.2I-HFEM的实现

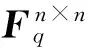
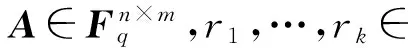
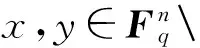
(ab)[r1，r2]=(a[r1，r2])b=(x1A1[r1，r2]+…+xnAn[r1，r2])(y1B1+…+ynBn)=T[r1，r2].

由此可得Fq上具有2n个变元和2n个方程的BMQ方程组E(A[r1，r2]，B，T[r1，r2])：

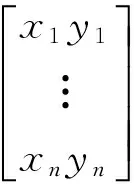
由E(A[r1，r2]，B，T[r1，r2])的构造，可知其恰好对应于E(A，B，T)中的第(r1-1)n+1至r1n以及第(r2-1)n+1至r2n这2n个方程，即E(A[r1，r2]，B，T[r1，r2])为E(A，B，T)的“子方程组”.又由Rank(AB)=2n和相关定理可知，必存在i，j∈{1，…，n}，且E(A[i，j]，B，T[i，j])中的2n个方程彼此线性无关.所以E(A[i，j]，B，T[i，j]必与E(A，B，T)等价，即二者同解.

令(A′=A[i，j]={A1[i，j]，…，A[i，j]}，B′=B)，则(A′，B′)满足所有的新约束条件.由此可实现I-HFEM.

密钥生成部分：

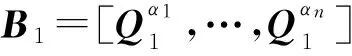
(5) 如果Rank([AB])<2n，则转(4)；

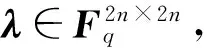
(7) 由RAB生成2n个Fq上的BMQ多项式ρk(x，y)=Rk[x⊗y](1≤k≤2n)；

(8) 公钥为(Fq，ρ=[ρ1(x，y)，…，ρ2n(x，y)]，私钥为(A，B，λ).

解密部分：

(3) 如果T[1]≠0，则令k=1，否则令k=2；

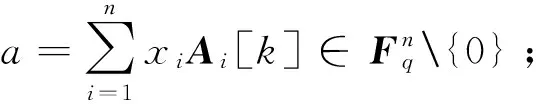
(6) 由(x，y)还原出明文P=x⊗y=α⊗β.

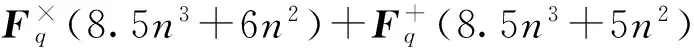
2.3I-HFEM与HFEM的主要区别

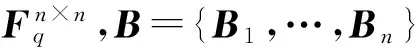
3 基于I-HFEM的数字签名方案设计

设签名者Peggy的公钥和私钥分别为(Fq，ρ=[ρ1(x，y)，…，ρ2n(x，y)]和(A，B，λ)，则Peggy和验证者Vic可按如下方式对消息进行签名和验证签名.

签名为：

(5) (H，sm)即为Peggy对消息m的签名.

验证签名为：

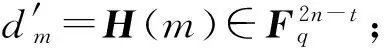
(2) Vic用Peggy的公钥计算d″m=(ρ1(sm)，…，ρ2n-t(sm))；

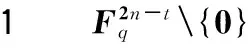
表中无法被签名的消息摘要数量及所占比例

注：100次实验结果.

由表1可以看出如下规律：

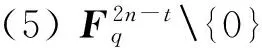
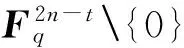
[1] 赵永哲，赵博，裴士辉，等.HFEM公钥密码方案的设计与实现[J].通信学报，2011，32(6)：24-31.

[2] 赵博，赵宏伟，苏晋璇，等.MPKC的中心映射与公钥形式[J].吉林大学学报：理学版，2012，50(4)：719-725.

[3] 裴士辉，赵永哲，赵宏伟.基于遍历矩阵的公钥加密方案[J].电子学报，2010，38(8)：1908-1913.

[4] 赵永哲，赵搏，裴士辉.有限域上遍历矩阵的特性研究[J].数学学报，2012，55(3)：457-468.

[5] 袁哲，赵永哲，李光伟，等.利用有限域上遍历矩阵实现基于隐藏基的密钥交换[J].吉林大学学报：理学版，2009，47(04)：783-789.

[6] 赵永哲，黄声烈，姜占华.GF(2k)上的遍历矩阵及其特性分析[J].小型微型计算机系统，2005，26(12):2135-2139.

[7] 赵永哲，姜占华，黄声烈.基于F2上遍历矩阵的Sham ir三次传递协议的实现[J].小型微型计算机系统，2006，27(6):986-991.

[8] 孙永雄，赵永哲，杨永健，等.基于遍历矩阵的单向(陷门)函数的构造方案[J].吉林大学学报:信息科学版，2006，24(5):555-560.

[9] 赵永哲，裴士辉，王洪军，等.利用有限域上的遍历矩阵构造动态加密器[J].小型微型计算机系统，2007，28(11):2010-2014.

Abstract:This paper explores the decipherment efficiency in the HFEM public key cryptography plan，puts forward the improved HFEM public key cryptography plan (I-HFEM)，gives the definition and algorithm，proves that the private key size of I-HFEM plan and the decipherment cost will have a great reduction than the original one，and illustrates that I-HFEM plan has very important applied significance in the field of digital signature.

Keywords:HFEM public key cryptography；HFEM；I-HFEM；signature plan；ergodic matrices over the finite field

(责任编辑：石绍庆)

The application design of improved HFEM public key cryptography plan on signature

SONG Yan1，ZHAO Yong-zhe2

(1.Center of Network，Changchun Normal University，Changchun 130032，China；2.School of Computer Science and Technology，Jilin University，Changchun 130012，China)

1000-1832(2014)03-0069-06

10.11672/dbsdzk2014-03-014

2013-07-11

“十一五”国家密码发展基金资助项目(2006L014J00002)；吉林省教育厅科学技术研究项目(吉教科合字[2008]第346号).

宋严(1982—)，男，硕士，实验师；赵永哲(1961—)，男，硕士，教授，主要从事密码学和信息安全研究.

TN 915.08 [学科代码] 520·1060

A