滚仰式导引头稳定平台动力学建模及驱动力矩计算

刘 慧，朱明超，高思远，张宏巍，吴泽鹏

(1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.上海卫星工程研究所，上海 200240)

滚仰式导引头稳定平台动力学建模及驱动力矩计算

刘 慧1，朱明超1，高思远1，张宏巍1，吴泽鹏2

(1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.上海卫星工程研究所，上海 200240)

为指导滚仰式导引头稳定平台控制系统的设计，结合李群理论，分析了稳定平台运动学描述方法，推导了广义坐标形式的动力学方程.该动力学方程不仅考虑了加速度力矩，而且综合了质量不平衡力矩、框架耦合力矩及弹体运动产生的干扰力矩等非线性力矩.在此基础上分析了导引头跟踪沿光轴切线飞行的目标时的角速度、角加速度参数.最后针对某滚仰式导引头原理样机，数值计算滚转轴的最大驱动力矩为1.828 N·m，俯仰轴最大驱动力矩为0.015 6 N·m.

滚仰式导引头；动力学建模；驱动力矩计算

0 引言

随着制空权在现代战争中地位的显著提升，空空导弹也逐渐发展为导弹家族中至关重要的一员.导引头是空空导弹的关键组成部分，其机构主要有俯仰-偏航式、滚转-俯仰式(以下简称滚仰式)、三框架式等.滚仰式导引头体积小、质量轻，并可实现前半球视场的搜索，极大提高了空空导弹的搜索和跟踪能力[1-3]，滚仰式伺服结构因此成为当今空空格斗导弹导引头稳定平台的理想选择.

美国的AIM-9X、欧洲的IRIS-T空空导弹均采用滚仰式结构的导引头，目前已装备美欧空军.以上两款导引头比传统导引头均具有更快的跟踪速度、更高的稳像和跟踪精度[4]，总之该结构对控制系统的要求很高，而系统运动学、动力学的研究以及稳定平台框架轴角运动参数确定、驱动力矩计算是认清稳定平台系统的工作机理、选择合适的驱动电机、实现平台稳定控制的基础.

针对上述问题，本文首先针对滚仰式导引头的结构特点，结合李群理论，分析了框架的运动学描述方法，推导了基于几何形式的Newton-Euler动力学方程，然后确定了框架角速度、角加速度运动参数，最后针对某滚仰式导引头样机给出了详细的力矩计算曲线.

1 滚仰式稳定平台运动学分析

图1为采用的滚仰式导引头的结构原理图.采用滚转外框架、俯仰内框架结构，其中外框架滚转轴与弹体纵轴一致，内框架俯仰轴与外框架滚转轴正交.外框架可以实现n×360°滚转，内框架俯仰范围可以达到±90°，其中光学系统及其探测器安装在俯仰框上，2个框架通过轴承连接在一起，由独立的直接耦合的力矩电机驱动，并使用高精度光电编码器来测量平台相对弹体在滚转和俯仰方向的轴向角偏差，安装的速率陀螺分别敏感平台相对惯性空间的角速率，以完成稳定跟踪.

为建立稳定平台的动力学模型，建立如图2所示的坐标系统.其中：坐标系0为弹体坐标系；坐标系1为滚转坐标系，与滚转轴x1固联，滚转角为θ1；坐标系1*的坐标分量与坐标系1平行；坐标系2为俯仰坐标系，与俯仰轴z2固联，俯仰角为θ2，x2方向为光轴指向；坐标系2*的坐标分量与坐标系2平行.

图1 滚仰式导引头结构图

图2 滚仰式稳定平台运动学坐标系与质心坐标系

由图2所示的坐标系统，导引头的运动学方程为[5-6]

(1)

(2)

(3)

其中ωi=[ωix，ωiy，ωiz]T为坐标系i下描述的旋转轴线方向的单位矢量；vi=[vix，viy，viz]T定义为

vi=ωi×li.

(4)

在上式中，li是旋转轴线上任意一点.

ξi= [ωi；vi].

(5)

2 滚仰式稳定平台动力学建模

关于质心坐标系i*的广义坐标形式的Newton-Euler方程可以描述如下[7-8]

(6)

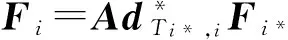
(7)

(8)

(9)

(10)

把公式(7)—(10)代入公式(6)得到框架i相对于坐标系i的Newton-Euler方程

(11)

在公式(11)中：Ji∈R6×6为广义质量矩阵，表示为

(12)

(13)

经两步Newton-Euler迭代算法，在正解迭代过程中，广义速度和广义加速度从弹体坐标系向滚转坐标系再向俯仰坐标系逐级传递，在反解迭代过程中，广义力从俯仰坐标系向滚转坐标系逐级传递.

(1) 初始化

(2) 正向迭代

(14)

(15)

(16)

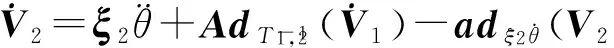
(17)

(3) 反向迭代

(18)

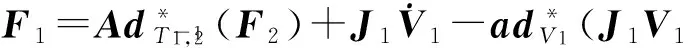
(19)

施加到坐标系i上的力矩计算公式为

(20)

将以上式子扩展为全局矩阵描述，最后可得导引头封闭形式的动力学方程

(21)

3 滚仰式稳定平台最大角速度和角加速度的确定

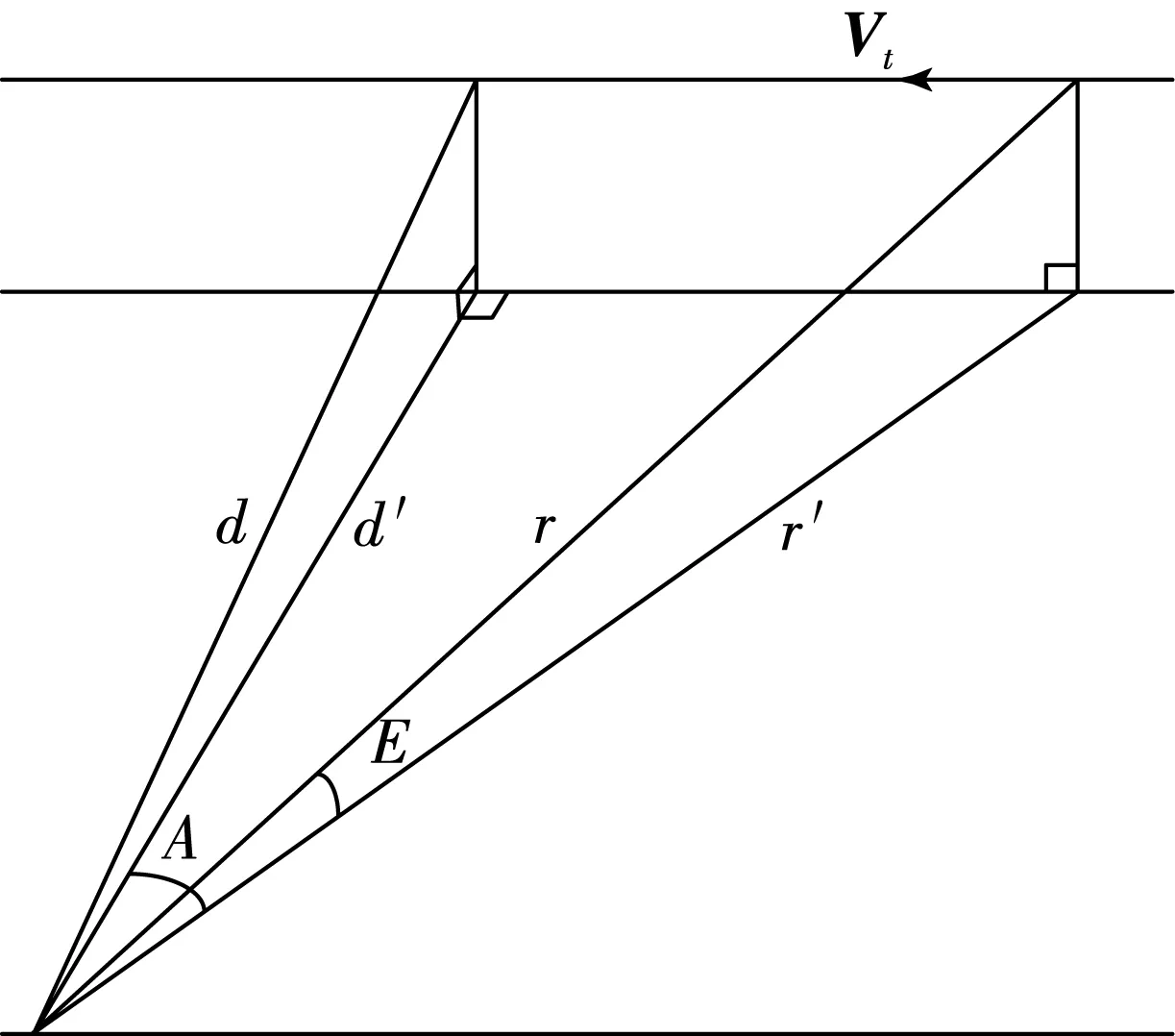
图3 滚仰式导引头稳定平台跟踪目标示意图

滚仰式稳定平台动力学模型如进行数值计算需获得框架角速度、角加速度运动参数，而这些参数是根据其预定执行的任务来确定的[9].便于分析和计算，对导引头跟踪目标过程做一些简化，假设目标在滚仰式导引头稳定平台光轴的正前方，沿光轴的切线方向运动，速度为Vt，目标的最短距离为rmin(d)，而一般情况下很少出现此极限跟踪难度的情况，而是目标速度在光轴方向有投影分量，故这样分析出的结果给实际情况留有一定裕量.通过一个虚拟的俯仰角E和偏航角A可以使光轴指向目标，如图3所示.

通过几何关系可知：

(22)

(23)

由几何关系不难得出，虚拟俯仰角E、偏航角A和光轴指向目标时的滚转角θ1、俯仰角θ2之间的关系为：

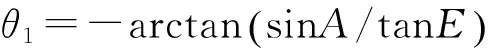
(24)

(25)

(26)

(27)

对上式中θ1和θ2求导，则滚转和俯仰角速度应为：

(28)

(29)

同理，可得滚转和俯仰角加速度为：

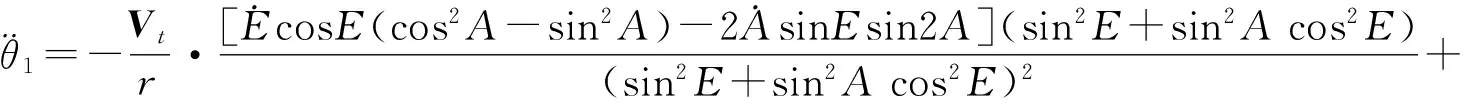
(30)

(31)

滚仰式导引头跟踪的典型目标为战斗机，根据总体技术指标推算，沿光轴切线方向目标速度为Vt=300 m/s，弹目最短距离为r=1 000 m，最小俯仰角(天顶角)为θmin=0.02 rad，由公式(22)—(31)可以计算滚转和俯仰角速度以及角加速度，计算结果如图4所示.

(a) 滚转角速度曲线 (b) 滚转角加速度曲线

(c) 俯仰角速度曲线 (d) 俯仰角加速度曲线

图4 滚转和俯仰角速度以及角加速度曲线

由曲线可得滚仰式导引头跟踪目标需要的最大滚转角速度、角加速度分别为14.99 rad/s和216.92 rad/s2；最大俯仰角速度、角加速度分别为0.281 7 rad/s和4.50 rad/s2.以上曲线数值是动力学力矩计算需要的参数，同时获得的角速度可作为驱动电机转速选取的理论依据.

4 滚仰式导引头框架轴驱动力矩计算

某滚仰式导引头样机的结构参数如下：

滚转框质量(质心系)：m1=2.356 kg，

滚转框转动惯量(质心系)：I1=diag(0.080 52，0.072 51，0.092 76) kg·m2；

俯仰框质量(质心系)：m2=0.245 kg，

俯仰框转动惯量(质心系)：I2=diag(0.000 091，0.000 118，0.000 471) kg·m2；

滚转框质心在滚转坐标系中的矢径：[0，0.001，0.002]Tm；

俯仰框质心在俯仰坐标系中的矢径：[0.002，0.001，0]Tm.

滚仰式导引头的载体一般为近距格斗型空空导弹，目标一般为战斗机，发射前锁定，根据总体提供的载体导弹击中目标全过程的弹道数据，为不失一般性，取离轴发射初始阶段最严酷的一点弹体数据作为输入.弹体角速度为[0，1.5，3.0]Trad/s，角加速度为[0，17.5，31.0]Trad/s2；弹体线速度为[496，87.6.5，46.2]Tm/s，线加速度为[7.5，180.0，345.2]Tm/s2.

(a)滚转框加速度力矩 (b) 滚转框哥氏力矩 (c) 滚转框弹体运动产生的干扰力矩

图5 滚转框各项力矩曲线

(a)俯仰框加速度力矩 (b) 俯仰框哥氏力矩 (c) 俯仰框弹体运动产生的干扰力矩

图6 俯仰框各项力矩曲线

5 结论

本文首先推导了基于广义坐标形式的滚仰式导引头动力学方程，同时为完成框架轴驱动力矩数值计算，确定了导引头跟踪正前方沿光轴切线飞行的目标时的角速度、角加速度运动参数，最大滚转角速度、角加速度分别为14.99 rad/s和216.92 rad/s2，最大俯仰角速度、角加速度分别为0.281 7 rad/s和4.50 rad/s2，最后针对某滚仰式导引头原理样机，计算出滚转框需要总的最大驱动力矩为1.828 N·m，俯仰框需要总的最大驱动力矩为0.015 6 N·m.

[1] 张鑫，贾宏光.90°离轴角红外滚仰式导引头光学系统[J].红外与激光工程，2013，42(1)：143-144.

[2] 王志伟，祁载康，王江. 滚-仰式导引头跟踪原理[J].红外与激光工程，2008，37(2)：274-277.

[3] JIANG H H，JIA H G，WEI Q. Analysis of zenith pass problem and tracking strategy design for roll-pitch seeker[J]. Aerospace Science and Technology，2012，23：345-351.

[4] 穆学桢，周树平，赵桂瑾.AIM-9X空空导弹位标器新技术分析和评价[J].红外与激光工程，2006，35(4)：392-394.

[5] CHEN I，YANG G，TAN C，et al. Local POE model for robot kinematic calibration [J]. Mechanism and Machine Theory，2001，36(11/12)：1215-1239.

[6] MAMPETTA A K. A Lie group formulation of kinematics and Dynamics of serial manipulator[J]. Mechanics of Manipulation，2006：16-741.

[7] HWANG Y L. Recursive Newton-Euler formulation for flexible dynamic manufacturing analysis of open-loop robotic systems[J]. International Journal of Advanced Manufacturing Technology，2006，29(5/6)：598-604.

[8] FRANK C PARK，JAMES E BOBROW. A recursive algorithm for robot dynamics using Lie groups[J]. IEEE International Conference on Robotics and Automation，1994：1535-1540.

[9] 王广雄，何朕.控制系统设计[M].北京：清华大学出版社，2008：36-41.

Abstract:The kinematics representation of POE formula and dynamics model of generalized coordinate based on Lie group theory for roll-pitch seeker were researched to design the stabilized platform control system. This dynamics model not only considered inertial torque，but also included some nonlinear torque such as mass imbalance torque，biaxial coupling torque，and the disturbed torque of missile movement. Then the motion parameters of angular velocity and angular acceleration were analyzed when the roll-pitch seeker tracking the target of fly straight and level. Based on a certain principled prototype of roll-pitch seeker，the total maximum driving torques of roll axis and pitch axis were numerically calculated，which were 1.828 and 0.015 6 N·m accordingly. The result provides a theoretical reference for the drive motor selection，and more importantly，this research can set up a foundation for the further high precision control system design.

Keywords:roll-pitch seeker；dynamics modeling；driving torque calculation.

(责任编辑：石绍庆)

Dynamics modeling and driving torque calculation for stabilized platform of roll-pitch seekers

LIU Hui1，ZHU Ming-chao1，GAO Si-yuan1，ZHANG Hong-wei1，WU Ze-peng2

(1.Changchun Institute of Optics Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Shanghai Institute of Satellite Engineering，Shanghai 200240，China)

1000-1832(2014)03-0081-06

10.11672/dbsdzk2014-03-016

2014-02-18

中国科学院“三期创新”平台资助项目；吉林省科技发展计划项目(20100458).

刘慧(1983—)，男，博士，助理研究员，主要从事导引头运动学、动力学与控制研究.

TP 336；V 249 [学科代码] 510·50

A