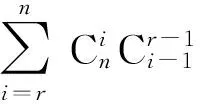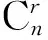半群POn中理想的非群元秩和相关秩

罗永贵，瞿云云

(贵州师范大学数学与计算机科学学院，贵州 贵阳 550001)

半群POn中理想的非群元秩和相关秩

罗永贵，瞿云云

(贵州师范大学数学与计算机科学学院，贵州 贵阳 550001)

设POn是有限链[n]上的保序部分奇异变换半群.对任意的r(2≤r≤n-1)，考虑半群M(n，r)={α∈POn：|Imα|≤r}的非群元秩和非幂等元秩.证明了M(n，r)是由秩为r的元素生成的.确定了当0≤l≤r时，半群M(n，r)关于其理想M(n，l)的相关秩.

部分保序；奇异变换半群；非群元秩和非幂等元秩；相关秩

0 引言

设S是半群，G是S的子群，A是S的一个非空子集，α，ε∈S.若G是S的真子群，对S的任意子群T，由G⊆T可推出G=T，则称G是S的极大子群.若存在S的一个极大子群G，使得α∈G，则称α是S的一个群元素；否则称α是S的一个非群元素.S中所有群元素之集记为G(S).若ε2=εε=ε，则称ε是S的一个幂等元；否则称ε是S的一个非幂等元.A中所有幂等元之集记为E(A).易见，半群S中的幂等元一定是群元素，但群元素不一定是幂等元；非群元素一定是非幂等元，但非幂等元不一定是非群元素.

通常一个有限半群S的秩定义为rank(S)=min{|A|：A⊆S，〈A〉=S}.如果S是由幂等元之集E(S)生成的，那么S的幂等元秩定义为idrank(S)=min{|A|：A⊆E(S)，〈A〉=S}.如果S是由非幂等元之集SE(S)生成的，那么S的非幂等元秩定义为Nidrank(S)=min{|A|：A⊆(SE(S))，〈A〉=S}.如果S是由群元素之集G(S)生成的，那么S的群元秩定义为Grank(S)=min{|A|：A⊆G(S)，〈A〉=S}.如果S是由非群元素之集SG(S)生成的，那么S的非群元秩定义为NGrank(S)=min{|A|：A⊆(SG(S))，〈A〉=S}.半群S及其子半群V之间的相关秩定义为r(S，V)=min{|A|：A⊆S，A∩V=∅，〈A∪V〉=S}.易见，半群S中的幂等元秩一定是群元秩，但群元秩不一定是幂等元秩；非群元秩一定是非幂等元秩，但非幂等元秩不一定是非群元秩.rank(S)≤idrank(S)，r(S，S)=0.对于有限半群的秩、幂等元秩、非幂等元秩及其相关秩的研究目前已有许多结果[1-8].

设[n]={1，2，3，…，n-1，n}(n≥3)并赋予自然数的大小序.Pn，In与Sn分别表示[n]上的部分变换半群，对称逆半群和对称群，SPn=PnSn是[n]上的部分奇异变换半群.设α∈SPn，若对任意的x，y∈domα，x≤y⟹xα≤yα，则称α是部分保序的.记POn为[n]上的所有部分保序奇异变换构成的集合.显然，POn是SPn的子半群，称为保序有限部分奇异变换半群.记

M(n，r)={α∈POn：|Imα|≤r}(0≤r≤n-1)，

本文在文献[1-2]的基础上继续考虑保序有限部分奇异变换半群POn的双边理想M(n，r)的非群元秩和相关秩，证明了如下结果：

定理1 设n≥3，0≤r≤n-1，则Jr是M(n，r)的生成集，即M(n，r)=〈Jr〉.

定理3 设n≥3，0≤l≤r≤n-1，则

设P，Q是自然序集[n]的非空子集，若对任意的a∈P，b∈Q有a

其中，A1

为叙述方便，这里引用Green-等价关系[9].不难验证，在半群M(n，r)中，L，R，J有如下刻画：对任意的α，β∈M(n，r)，

(α，β)∈L⟺Imα=Imβ，
(α，β)∈R⟺Kerα=Kerβ，
(α，β)∈J⟺|Imα|=|Imβ|.

本文未定义的术语及符号参见文献[10-12].

1 预备知识

为完成定理的证明先给出若干引理与推论.

引理1 对0≤k≤1，有Jk⊆Jk+1·Jk+1.

情形1 若|A|=1，注意到n≥3，可设A={b}，取c∈[n]{b}.

若b

若b>c.

情形2 若|A|>1，记x=minA.

综上所述，对0≤k≤1，有Jk⊆Jk+1·Jk+1.

引理2 对2≤k≤r-1，3≤r≤n-1，有Jk⊆Jk+1·Jk+1.

证明 对任意的α∈Jk，设α的标准表示为

其中，A1

以下分两种情形证明存在β，γ∈Jk+1，使得α=βγ.

情形1 若存在i∈{1，2，…，k-1，k}，使得|Ai|≥2，记x=minAi.

情形1.1 若a1≠1，令

则β，γ∈Jk+1且α=βγ.

情形1.2 若ak≠n，令

则β，γ∈Jk+1且α=βγ.

情形1.3 若a1=1且ak=n，结合2≤k≤n-2知，存在j∈{2，3，…，k-1，k}，使得aj-aj-1>1.

如果i

如果i=j，令

如果i>j，令

则β，γ∈Jk+1且α=βγ.

情形2 若对任意的i∈{1，2，…，k-1，k}都有|Ai|=1，不妨设Ai={bi}，则

并且b1

情形2.1 若b1≠1且a1≠1，令

则β，γ∈Jk+1且α=βγ.

情形2.2 若b1≠1且ak≠n，令

则β，γ∈Jk+1且α=βγ.

情形2.3 若b1≠1且a1=1，ak=n，由2≤k≤n-2知，存在j∈{2，3，…，k-1，k}，使得aj-aj-1>1，令

则β，γ∈Jk+1且α=βγ.

情形2.4 若bk≠n且a1≠1，令

则β，γ∈Jk+1且α=βγ.

情形2.5 若bk≠n且ak≠n，令

则β，γ∈Jk+1且α=βγ.

情形2.6 若bk≠n且a1=1，ak=n，由2≤k≤n-2知，存在j∈{2，3，…，k-1，k}，使得aj-aj-1>1，令

则β，γ∈Jk+1且α=βγ.

情形2.7 若b1=1，bk=n且a1≠1，由2≤k≤n-2知，存在j∈{2，3，…，k-1，k}，使得bj-bj-1>1，令

则β，γ∈Jk+1且α=βγ.

情形2.8 若b1=1，bk=n且ak≠n，由2≤k≤n-2知，存在j∈{2，3，…，k-1，k}，使得bj-bj-1>1，令

则β，γ∈Jk+1且α=βγ.

情形2.9 若b1=1，bk=n且a1=1，ak=n，注意到2≤k≤n-2知，存在j，i∈{2，3，…，k-1，k}，使得bj-bj-1>1，ai-ai-1>1.

如果i

如果i=j，令

如果i>j，令

则β，γ∈Jk+1且α=βγ.

2 定理的证明

2.1 定理1的证明

由引理1和引理2可知，对任意的α∈M(n，r)都可以表达成M(n，r)的顶端J-类Jr中秩为r的若干元素的乘积或者α∈Jr.即Jr是M(n，r)的生成集，M(n，r)=〈Jr〉.

引理3 设α∈M(n，r)，则下列条件等价：

(1)α是幂等元；

(2) 对任意的t∈Imα有t∈tα-1；

(3)α|Imα是恒等变换.

证明 (1)⟹(2) 若α是幂等元，则α2=α.进一步，对任意的y∈domα，有(yα)α=yα2=yα可知yα∈(yα)α-1.令t=yα，即对任意的t∈Imα，有t∈tα-1.

(2)⟹(3) 是显然的.

(3)⟹(1) 若α|Imα是恒等变换，则对任意的y∈domα，有yα2=(yα)α=yα，由此可知α2=α，则α是幂等元.

引理4[11]设ε是半群S的一个幂等元，则Hε是半群S的极大子群.

推论1 设n≥3，2≤k≤r≤n-1，对任意的

其中，A1

引理5 设n≥3，2≤k≤r≤n-1，则对任意的α∈Jk，必存在非群元素β∈(Jk∩(M(n，r)G(M(n，r))))，使得(α，β)∈R.

证明 对任意 的α∈Jk，设α的标准表示为

其中，A1

以下分两种情形证明存在非群元素β∈(Jk∩(M(n，r)G(M(n，r))))，使得(α，β)∈R.

情形1 若存在i∈{1，2，…，k-1，k}，使得|Ai|≥2.

如果i=1时，取b1，b2∈A1，b3∈A3，b4∈A4，…，bi-1∈Ai-1，bi∈Ai，bi+1∈Ai+1，…，bk-1∈Ak-1，bk∈Ak且b1

如果2≤i≤k时，取b1∈A1，b2∈A2，…，bi-2∈Ai-2，bi-1，bi∈Ai，bi+1∈Ai+1，…，bk-1∈Ak-1，bk∈Ak且bi-1

由推论1，可知β∈(Jk∩(M(n，r)G(M(n，r)))).再由Kerα=Kerβ可知(α，β)∈R.

情形2 若对任意的i∈{1，2，…，k-1，k}，使得|Ai|=1.不妨设Ai={ai}，则a1

如果b

如果存在i∈{2，3，…，k-1，k}，使得ai-1

如果b>ak，令

由推论1，可知β∈(Jk∩(M(n，r)G(M(n，r)))).再由Kerα=Kerα可知(α，β)∈R.

其次，对任意的α∈Jr，以下分两种情形验证α∈〈M〉，即Jr⊆〈M〉.

当i

当i=j时，有α=αi.

当j

当j

当j=p时，有α=βi.

当p

引理7 设α，β∈M(n，r)，若(α，β)∈J且(α，αβ)∈J，则(αβ，β)∈L，(α，αβ)∈R.

证明 设α，β∈M(n，r)，若(α，β)∈J且(α，αβ)∈J，则|Imα|=|Imβ|=|Imαβ|.再由Im(αβ)⊆Imβ，Kerα⊆Ker(αβ)与[n]的有限性知，Im(αβ)=Imβ，Kerα=Ker(αβ)，即(αβ，β)∈L，(α，αβ)∈R.

2.2 定理2的证明

2.3 定理3的证明

当l=r时，显然有r(M(n，r)，M(n，l))=0.

当0≤l

注2 由引理1的证明可知M(n，0)=J0=E(J0)={∅}.于是M(n，0)不存在非群元秩.

[1] GOMES G M S，HOWIE J M.On the ranks of certain semigroups of order-preserving transformations[J].Semigroup Forum，1992，45(1)：272-282.

[2] GARBA G U.On the idempotent ranks of certain semigroups of order-preserving transformations[J].Portugaliae Mathematica，1994，51(2)：185-204.

[3] XIULIANG YANG.Non-group ranks in finite full transformation semigroups[J].Semigroup Forum，1998，57：42-47.

[4] HOWIE J M，RUKUC N，HIGGINS P M.On relative ranks of full transformation semigroups[J].Communication in Algebra，1998，26(3)：733-748.

[6] 钟裕林，霍元极.奇异典型群作用下子空间轨道的长度[J].东北师大学报：自然科学版，2012，44(1)：36-40.

[7] 王秀丽.伪k-投射半模[J].东北师大学报：自然科学版，2012，44(1)：41-44.

[8] 陈松良.论Sylowp-子群循环的pnq3阶群的构造[J].东北师大学报：自然科学版，2013，45(2)：35-38.

[9] GREEN J A.On the structure of semigroups[J].The Ann of Math，1951，54(1)：163-172.

[10] HOWIE J M.Fundamentals of semigroup theory[M].Oxford：Oxford University Press，1995：1-64.

[11] GANYUSHKIN O，MAZORCHUK V.Classical finite transformation semigroups[M].London：Springer-Verlag，2009：1-89.

Abstract:LetPOnbe the semigroup of all order-preserving partial singular transformations on a finite-chain [n].For an arbitrary integerr(2≤r≤n-1)，the non-group rank and non-idempotent rank of the semigroupM(n，r)={α∈POn：|Imα|≤r} were studied.We proved thatM(n，r) is generated by elements of rankr.Furthermore，it is shown that for 0≤l≤r，the relative rank of the semigroupM(n，r) with respect to itself each idealM(n，l).

Keywords:partial order-preserving；singular transformation semigroup；non-group rank and non-idempotent rank；relative rank

(责任编辑：陶 理)

Non-group rank and relative rank of each ideal of the semigroupPOn

LUO Yong-gui，QU Yun-yun

(Department of Mathematics and Computer Science，Guizhou Normal University，Guiyang 550001，China)

1000-1832(2014)03-0020-08

10.11672/dbsdzk2014-03-005

2013-05-06

贵州省科学技术基金资助项目(黔科合J字LKS(2011)15号).

罗永贵(1985—)，男，硕士，讲师，主要从事半群代数理论研究.

O 152.7 [学科代码] 110·21

A