基于LMD样本熵与SVM的往复压缩机故障诊断方法

邹龙庆，陈桂娟，邢俊杰，姜楚豪

（1.东北石油大学 机械科学与工程学院，黑龙江 大庆163318；2.北京联合大学 机电学院，北京100020）

基于LMD样本熵与SVM的往复压缩机故障诊断方法

邹龙庆1，陈桂娟1，邢俊杰1，姜楚豪2

（1.东北石油大学 机械科学与工程学院，黑龙江 大庆163318；2.北京联合大学 机电学院，北京100020）

针对往复压缩机振动信号的非平稳和非线性特性，提出了基于LMD样本熵与SVM的往复压缩机轴承间隙故障诊断方法。利用具有保形特性的Hermite插值法替代传统LMD中滑动平均法构造均值与包络函数，提高LMD对非平稳信号的分解精度。以改进LMD方法将各状态振动信号分解为一系列PF分量，依据相关性系数选择其中代表故障状态主要信息的PF分量，计算其样本熵形成有效的特征向量。使用SVM作为模式分类器，诊断得出轴承间隙故障类型。同LMD与近似熵方法所提取特征向量进行对比，结果表明本文方法具有更高的识别准确率。

振动与波；往复压缩机；LMD；样本熵；轴承；故障诊断

往复压缩机是用于压缩和输送气体的机械设备，已成为石油化工领域必不可少的关键设备，其传动机构轴承常因磨损出现间隙过大故障，致使整机振动超标而停机。然而，往复压缩机结构复杂，内部激励源众多，运动形式多样，其振动信号响应呈现强烈非平稳和非线性特性。以经典信号处理技术为基础的传统状态故障诊断方法对其进行故障诊断存在一定的局限性[1]。

英国学者Jonathan S.Smith于2005年提出了一种非平稳信号自适应分析方法——局部均值分解(Local Mean Decomposition,LMD)[2]。该方法能自适应地将一个复杂的多分量信号分解成若干个乘积函数(Production Function,PF)。LMD方法具有良好的非线性、非平稳信号分析能力，是往复压缩机振动信号的理想分析方法[3]。

LMD方法计算局部均值函数与包络估计函数有两种常用方法，分别是极值滑动平均法和极值上下包络线法。滑动平均法存在多次平滑后产生相位差，导致分解结果失真问题[4]。极值上下包络线法通常使用三次样条进行插值，但三次样条插值对强非平稳信号会出现过包络与欠包络现象。三次Hermite插值是一种较为常用的插值曲线构造方法，其仅要求节点一阶导数连续，具有优良的保形特性，尤其适合于具有强非平稳特性信号的包络[5]。因此，本文以其替代三次样条插值法构造LMD极值上下包络线。

近些年越来越多的非线性分析方法被用于机械设备故障诊断，如李雅普诺夫指数、分形维数和近似熵等。样本熵(Sample Entropy,Samp En)是一种用来描述时间序列复杂度的新方法，与近似熵、关联维数等非线性动力学方法相比，具有对所需的数据长度要求不高，抗噪声干扰能力强的特点[6,7]。往复压缩机振动信号呈现非线性，利用样本熵进行状态特征描述是可行的。但机械系统的信号随机性较大，且易受噪声的干扰，若仅采用样本熵法对其进行处理，会直接影响检测效果。所以，结合LMD方法，组合成一个混合的高性能算法，可提高样本熵算法在信号特征提取中的实际效果。

支持向量机(Support Vector Machine，SVM)是一种基于统计学习理论的模式识别方法，在解决非线性、小样本、高维模式识别以及局部极小等问题中存在诸多优势，已被广泛应用于机械设备故障诊断等领域[8]。

本文以往复压缩机轴承间隙故障为对象，首先，应用LMD方法对信号进行分解得出PF分量，通过相关系数法选择包含主要故障信息的PF分量；其次，以样本熵方法对其进行定量描述，形成特征向量；再者，以SVM作为模式分类器，实现轴承不同故障程度的诊断。

1 LMD方法

LMD方法实质是将原始信号分解为一系列乘积函数（PF分量）与残余分量之和，而每个PF分量均可表示为一个包络信号和一个纯调频信号的乘积，其中PF的瞬时幅值即为所对应的包络信号，瞬时频率则可以通过其对应的纯调频函数直接求出。本文使用三次Hermite插值对极值点进行插值，构造上下包络线，以替代滑动平均法求得局部均值函数和包络估计函数。对于任意信号x(t)，其算法步骤如下：

（1）找出原始信号x(t)的极值点序列nk，对其进行端点延拓，得到新的极值点序列Xk；

（2）利用三次Hermite插值法对极大值点进行插值，形成上包络线Emax，同样利用三次Hermite插值法对极小值点进行插值，形成下包络线Emin；

（3）利用下式即可计算得出局部均值函数m11(t)和包络估计函数a11(t)

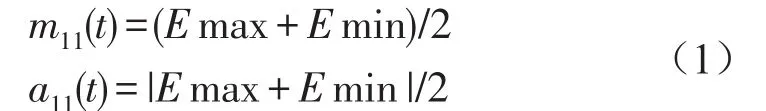
（4）从原始信号x(t)中分离出来局部均值函数m11(t)，即得h11(t)

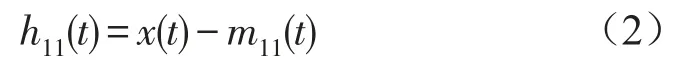
（5）用包络估计函数a11(t)除h11(t)，实现对h11(t)解调，即得s11(t)

再遵循以上步骤得出s11(t)的包络估计函数a12(t)，若a12(t)=1，则说明s11(t)为纯调频函数，若a12(t)≠1，则重复上述解调过程n次，直至s1n(t)的包络估计函数a1(n+1)(t)=1为止，也即s1n(t)为一个纯调频信号；

（6）把解调过程产生的所有包络信号相乘即得PF1的包络估计函数a1(t)

（7）将包络估计函数a1(t)与纯调频信号s1n(t)相乘即可得到第一个PF分量

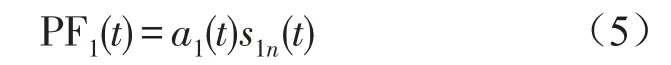
第一个PF分量是一个单分量的调频——调幅信号，包含了原始信号中最高的频率成分，其瞬时幅值就是包络估计函数a1(t)，其瞬时频率f1(t)则可由纯调频信号s1n(t)求出；

（8）将PF1(t)从原始信号x(t)中分离出来，得到一个新的信号u1(t)，将u1(t)作为原始信号重复以上步骤，循环k次，直到uk为单调函数为止，即

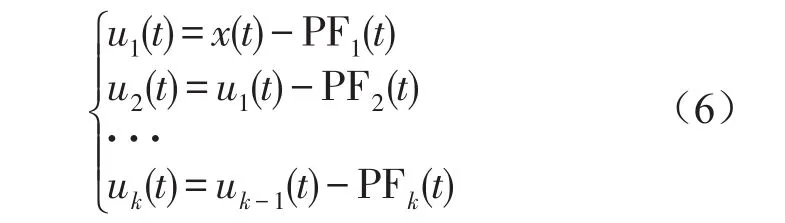
至此将原始信号x(t)分解为k个PF分量与一个uk之和，即

2 样本熵

一个时间序列{} x(i)|1≤i≤N由N个数据组成，{x(i)}=x(1)，x(2)，…，x(N)，样本熵的求解方法如下：

(1)选定一组m维矢量序列

Xm(1),…,Xm(N-m+1)，其中Xm(i)={x(i)，x(i+1)，…，x(i+m－1)}，1≤i≤N-m+1。

(2)将向量Xm(i)与Xm(j)两者对应元素中最大差值的绝对值定义为距离d[Xm(i),Xm(j)]，表示为

(3)给定r的阀值，统计Xm(i)与Xm(j)之间距离不大于r的j(1≤j≤N-m，j≠i)的数目，并记作Bi。对于1≤i≤N-m，表示为

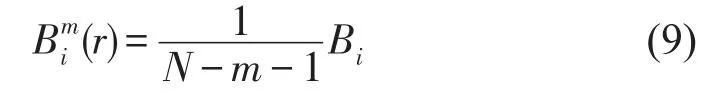
(4)定义Bm(r)为N-m个的平均值

(5)将维数增加为m+1，重复式(9)、式(10)，计算可得Bm+1(r)如下

在相似容限r下，Bm(r)与Bm+1(r)分别是匹配m和m+1个点的概率，则样本熵为

当N为有限值时，按上述步骤可得的时间序列样本熵的估计值为

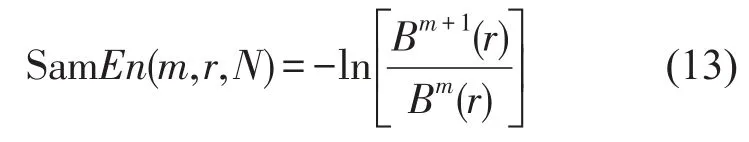
3 基于LMD样本熵与SVM的故障诊断方法

该方法通过LMD对信号进行分解，再选择包含主要故障信息的PF分量，以样本熵和SVM进行定量描述与故障识别，具体步骤如下：

(1)利用LMD方法对各状态信号进行分解，得到一系列PF分量；

(2)计算各个PF分量与原始信号的相关性系数，设定合理阈值选定能够代表状态主要信息的PF分量；

(3)计算各状态LMD分解结果中选定PF分量的样本熵，形成状态特征向量；

(4)以SVM作为模式分类器，识别当前状态特征向量所属故障类型。

4 往复压缩机轴承间隙故障诊断

2D12型往复压缩机的主要参数为：轴功率500 kW、排气量70 m3/min、活塞行程240 mm、电机转速496 r/min。磨损现象往往造成2D12压缩机传动机构的连杆轴承间隙过大，致使整机振动超标，进而停机，直接影响了生产效率。试验中，在2D12型压缩机传动机构的一级连杆大头轴承处分别模拟了正常、轻度磨损、中度磨损和重度磨损四种常见状态。根据压缩机结构特点，一级十字头滑道下端对轴承间隙故障状态敏感，使用加速度传感器采集该测点振动响应信号。数据采样频率50 kHz，采样时间4 s。利用与振动数据同步采集的键相信号，截取压缩机两旋转周期的振动数据进行分析。轴承重度磨损状态下测点的振动加速度时域信号如图1所示，可知由于轴承间隙的增大振动信号出现了规律的冲击现象。

图1 往复压缩机轴承重度磨损故障信号时域波形图

采用LMD方法将四种不同故障状态的振动信号分解为频率由高到低的PF分量，正常、轻度磨损、中度磨损和重度磨损四种状态分别分解出8、9、7和8个PF分量，而故障信息主要集中于前几个分量中。统计LMD分解结果中各个PF分量与原始信号的相关性系数，发现各状态前4个PF分量的相关性系数均大于0.15，基本体现了原始信号的信息特征。因此，本文选择各状态前4个PF分量进行样本熵计算，其中轴承重度磨损状态振动加速度信号经LMD方法分解的前4个PF分量如图2所示。

图2 三次Hermite插值LMD法的分解结果

不同的嵌入维数m和相似容限r对应的样本熵也不同。m和r的具体取值还没有一个最佳标准，一般m取1或2，r通常取0.1 SD～0.5 SD(SD为原始数据的标准差)，本文取m=2，r=0.15 SD。选取数据长度对应的时间应大于1个运行周期，本文选择两周期对应的数据，鉴于50 kHz频率采样数据点过多，计算量过大，对其进行5 kHz重采样，数据长度为1 209点。不同故障典型振动信号LMD分解结果中前4个PF的样本熵如表1所示。

SVM是一种基于统计学习理论的模式识别方法，并已被推广应用到模式识别等机器学习问题中[4]。台湾林智仁副教授开发的SVM工具包LibSVM集成了参数寻优、模型训练和结果测试等功能。

核参数和误差惩罚参数C是影响SVM性能的主要因素。本文所应用的径向基核函数具体形式为：K(x,xi)=exp{-γ‖x-xi‖2}，其中，核参数为γ。分别选取4种故障程度的各40组振动信号，利用本文方法进行特征提取构成训练样本集，应用Lib SVM的遗传算法对参数进行优化并建立SVM，优化结果为误差惩罚参数C取1.84，核参数γ取3.34。再随机选取4种故障程度的各40组特征向量样本对构建的SVM进行测试，各故障状态识别结果如表2所示。

为检验该方法的有效性，同样选取上述4种故障程度的各40组振动信号，以LMD分解结果中前4个PF分量的信息熵作为特征向量构成训练样本集，其中各故障典型特征向量如表1所示。以该样本集建立支持向量机，同样选取4种故障程度的各40组特征向量样本进行测试，结果仍如表2所示。通过比较两种方法的识别结果可知，对于相同有限数量的样本，LMD与样本熵特征向量明显高于LMD与信息熵特征向量的识别率，验证了本文方法的优越性。

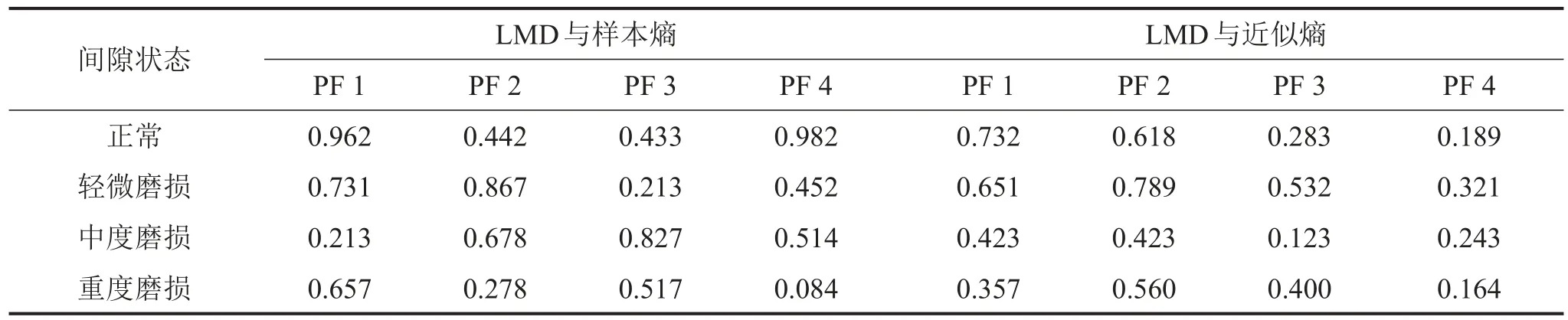
表1 不同特征提取方法的典型特征向量

表2 不同方法提取特征向量的识别结果

5 结语

针对往复压缩机振动信号具有的非平稳和非线性特性，本文提出了基于LMD样本熵与SVM的故障诊断方法。利用Hermite插值构造LMD方法的局部均值函数与包络估计函数，并进行往复压缩机不同轴承故障状态振动信号分解，依据相关性系数选择了LMD分解结果中代表故障主要信息的前几个PF分量，实现了信息约简，突出了状态信息。以样本熵定量描述各状态PF分量形成了特征向量，并以SVM作为模式分类器识别了故障类型，和LMD与近似熵方法所提取特征向量进行对比，结果表明，本文方法具有更高识别准确率，为往复压缩机故障诊断提供了一种新途径。

[1]赵海洋，徐敏强，王金东.基于多重分形与奇异值分解的往复压缩机故障特征提取方法研究[J].振动与冲击，2013，32(23)：110-114.

[2]Jonathan S Smith.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5)∶443-454.

[3]张亢，程军圣，杨宇.基于有理样条函数的局部均值分解方法及其应用[J].振动工程学报，2011，24(1)：97-103.

[4]徐继刚，赵荣珍，朱永生，等.局部均值分解在旋转机械复合故障诊断中的应用[J].噪声与振动控制，2012，32 (5)：144-149.

[5]张俊红，刘昱，毕凤荣，等.基于LMD和SVM的柴油机气门故障诊断[J].内燃机学报，2012，30(5)：469-473.

[6]赵志宏，杨绍普.一种基于样本熵的轴承故障诊断方法[J].振动与冲击，2012，31(6)：136-140.

[7]朱可恒，宋希庚，薛冬新.一种基于层次熵和SVM的轴承故障诊断方法[J].噪声与振动控制，2013，33(6)：163-167.

[8]赵海洋，徐敏强，王金东.改进二叉树支持向量机及其故障诊断方法研究[J].振动工程学报，2013，26(5)：764-770.

Fault Diagnosis Method Based on LMD Sample Entropy and SVM for Reciprocating Compressors

ZOU Long-qing1,CHEN Gui-juan1,XING Jun-jie1,JIANG Chu-hao2

(1.Mechanical Science and Engineering Institute,Northeast Petroleum University, Daqing 163318,Heilongjiang China; 2.College of Mechanical and Electrical Engineering,Beijing Union University,Beijing 100020,China)

∶Due to the non-stationary and nonlinearity characteristics of vibration signal of reciprocating compressors,a fault diagnosis method for bearing fault of reciprocating compressor based on LMD sample entropy and SVM is proposed.To improve the envelope approximation accuracy of local mean and envelope estimation,a cubic Hermite interpolation method,which has excellent conformal characteristic,is used to construct the envelope curves for the extreme points.Vibration signals in each state are decomposed into a series of PF components with the improved LMD method,and the PF components,which contain the main information of the fault state,are chosen according to the correlation coefficient.Sample entropy of the selected PF components is calculated as eigenvectors.Taking SVM as pattern classifier,the type of bearing clearance fault is diagnosed,and the advantage of this method is proved by comparing the eigenvectors extracted by LMD with those by the approximate entropy method.

∶vibration and wave;reciprocating compressor;LMD;sample entropy;bearing;fault diagnosis

TH212；TH213.3< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.039

1006-1355(2014)06-0174-04

2014-05-05

国家科技支撑计划项目（2012BAH28F03）；黑龙江省教育厅科学技术研究重点项目（12521051）；黑龙江省自然基金项目（E201335）

邹龙庆(1962-)，男，辽宁复县人，教授，博士生导师。现主要从事石油装备的设计理论及性能检测研究。

陈桂娟，女，博士生，讲师。

E-mail∶cgj2004@126.com