基于空间相关与自适应滤波的齿轮箱故障诊断

周继威

（中能电力科技开发有限公司，北京100034）

基于空间相关与自适应滤波的齿轮箱故障诊断

周继威

（中能电力科技开发有限公司，北京100034）

振动信号作为风电机组齿轮箱故障诊断的重要依据，一直是风电机组故障诊断领域关注的研究热点。基于不同频率、不同能量振动信号的传播规律，对齿轮箱上不同测点的振动信号的相关性进行分析，建立以互相关信号为参考信号的自适应滤波模型，利用该模型提取振动信号中的相似成分，进而利用幅值谱分析相似成分，得到更加清晰的转频及其倍频，为齿轮箱的故障诊断提供依据。方法的有效性得到实测振动数据的验证。

振动与波；故障诊断；齿轮箱；相关分析；自适应滤波；振动信号

随着能源危机与环境污染的日益严重，风能作为可再生绿色能源，近几年得到了广泛关注和迅猛开发。根据世界风能协会的报告，截止到2013年7月，全球装机总量已达318 GW，其中，中国的装机总量为80.824 GW，占全球装机总量的25.4%，是全球装机量最大的国家[1]。根据中国能源发展报告[2]，到2050年，中国风机装机容量将达到1 000 GW，满足17%的电力需求。

随着风机容量的不断增加，利用齿轮箱进行增速的双馈式风力发电机组（DFIG）降低了对发电机工艺的要求，因此市场份额占到了50%以上[3]。齿轮箱作为DFIG风力发电机组上的重要传动装置，由轴承、齿轮和传动轴等多个部件组成。由于加工工艺复杂，且工作环境恶劣，导致齿轮箱易发生故障。齿轮箱的故障发生率随着在役时间的增长逐年增高，故障百分比已超过机械传动系统总故障的60%，是机组中故障发生率最高的机械部件[4]。如果能够及早的发现齿轮箱中存在的故障，合理安排维护，对提高风力发电机组的可靠性和使用寿命具有重要意义。

当前对齿轮箱进行故障诊断的依据信息主要有：温度、油液及振动信号，但主要的诊断手段依旧是振动分析技术[5]。齿轮箱在工作过程中，其振动信号常常被机器的结构振动信号和干扰噪声所污染，尤其是早期故障信号十分微弱，信噪比低，这使得现有方法的诊断性能受到了很大影响[6，7]，虚警率高。齿轮箱中包含多对齿轮的啮合，其振动信号会产生多模式混淆，以及振动信号传输路径复杂导致故障响应微弱。多对齿轮啮合的振动相互耦合造成振动明显的非线性、低频特征频率成分噪声污染严重等[8]。B.Widrow[9]提出了利用参考信号训练滤波器系数的自适应滤波方法，但该算法需要一个与原始信号时间相关的参考信号，因此许多学者提出了改进的方法。R.B.Randall[10]利用信号中干扰部分延迟一段后与原干扰信号不相关的假设，采用延迟信号作为参考信号的自适应滤波方法消除信号中的干扰。该种方式能够在一定程度上消除随机噪声的干扰，但对于周期性的干扰无法消除。G.Ibrahim[11]采用仿真信号作为参考信号对齿轮箱的振动信号进行自适应滤波，该种方法具有较好的滤波效果，但是需要建立振动信号的模型，模型的精确度直接影响了滤波的效果。

本文以风电机组齿轮箱为研究对象，对易产生故障的高速轴部位故障进行分析。在分析了齿圈、低速轴以及高速轴测点振动信号的相关性后，提出了以互相关成分为参考信号的自适应滤波方法，可有效的将原始信号分解为不同位置相互耦合的相似成分和无耦合的独立部分，通过幅值谱分析能够更清晰的表达故障特征，提高了齿轮箱早期故障诊断的精度。

1 空间相关法

1.1 振动测点的空间分布

齿轮箱的结构有多种形式，其中使用最多的有两种结构为：一级行星轮传动两级平行轴传动结构和两级行星轮传动一级平行轴传动结构。本文研究的是第一种结构的齿轮箱，其内部结构示意图如图1所示，图中行星轮系采用直齿轮传动，定轴传动采用斜齿轮传动。

图1 齿轮箱内部结构示意图

齿轮箱的振动主要由制造误差以及部件故障产生，不同部位的振动由于啮合频率不同而导致振动频率不同，高速轴（S1）产生的振动信号频率最大，低速轴（S2）次之，齿圈（S3）产生的振动信号频率最小。根据波的传播理论，在相同环境中，随着振动频率的增加，振动衰减率增大，波传播的距离减小[12]。因此，相同距离下，低频振动源对高频振动波源的振动波形影响较大，但高频振动源对低频振动波源的振动波形影响较小。

齿轮箱上振动测点位置示意图如图2所示，由于振动信号在传播过程中，低频信号衰减较慢，高频信号衰减较快，因此，S3和S2点的振动信号中的低频分量对S1点振动波形影响大，而S1点的高频分量对S3和S2点的影响较小。

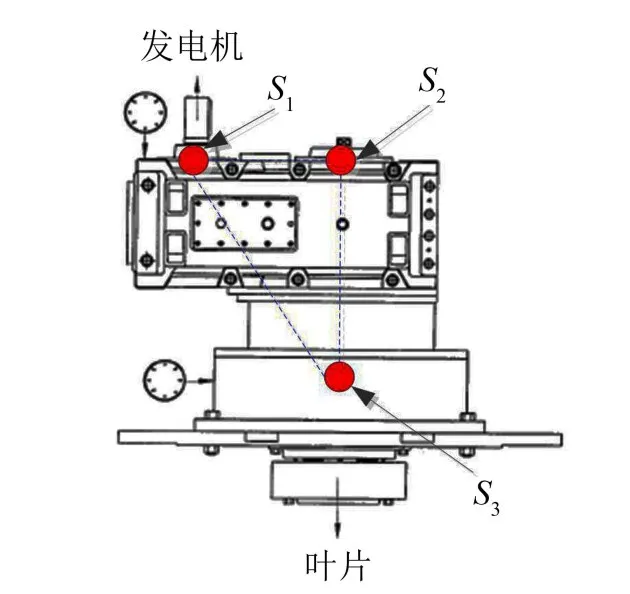
图2 齿轮箱振动测点位置示意图

在实际应用中，为了减小数据的在线传输和存储量，在线振动分析系统中不同测点的采样速率不同，S1测点为2 500 Hz，S2测点为1 000 Hz，S3测点为500 Hz，因此，在相似分量提取时需要对信号进行重采样。图3为重采样后的振动信号波形以及相应的幅值谱。从中可以看出，每个测点均包含55 Hz，110 Hz，330 Hz等频率成分，且该频率成分具有较大的能量。因此，不同测点的振动信号有一定的相关性。

1.2 相关分析法

相关函数是两个信号相似程度的一种度量，连续周期函数x(t)、y(t)的相关函数可以表示为

当x(t)和y(t)中含有相同的周期成分时，相关函数Rxy(τ)也含有相同的周期成分，进而通过相关分析可以得到两个平稳信号中的相似成分，而相关系数表明了两个函数的相关性的大小。两个信号分别为x(t)、y(t)的相关系数ρx,y表示为

其中cov(x,y)为x与y的协方差，D(x)和D(y)为x和y的方差。

离散信号x(n)和y(n)的互相关函数r^(m)表示为其中n=0,1,…,N-1

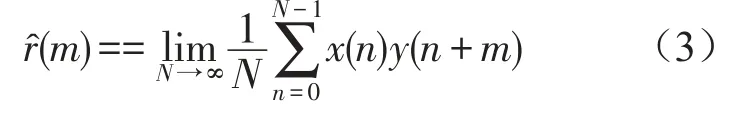
图3 齿轮箱振动信号

齿轮箱的振动信号在短时间内，可以认为是平稳的随机过程。通过对齿轮箱三个测点的信号进行相关分析，得出相关系数（如表1所示）和相关信号（如图4所示）。图中，a代表齿圈与高速轴振动信号的互相关信号（c1）；b代表低速轴与高速轴振动信号的互相关信号（c2）；c代表齿圈与低速轴振动信号的互相关信号（c3）。从中可以看出，高速轴信号与低速轴和齿圈信号具有较多的相关成分。

2 最小均方自适应滤波

自适应滤波能够根据参考信号的变化自动的调节滤波器的系数，从而保证在未知参考信号特性的情况下将测量信号分解为与参考信号相似的成分和相异成分[13]。即通过参考信号与滤波器输出信号的误差来调节滤波器的系数，使滤波器输出与参考信号的误差最小，从而达到提取相似成分的目的。图5描述了自适应滤波器的结构形式。通过参考信号d(n)与滤波输出信号y(n)的差值e(n)对滤波器的增量ΔWn进行调整，进而改变滤波器的系数Wn，然后对信号x(n)进行滤波，得到y(n)，具体计算过程如下：

表1 振动信号的相关系数

图4 齿轮箱振动信号互相关分析

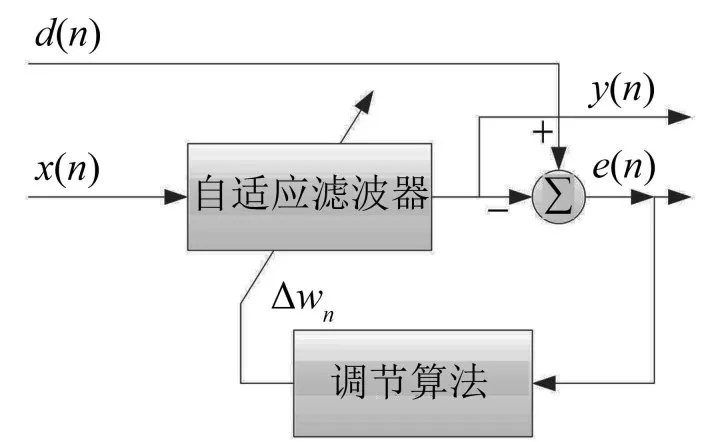
图5 自适应滤波器结构

假设：输入信号x(n)是参考信号d(n)和干扰噪声v(n)之和

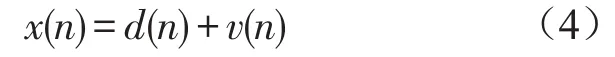
滤波器采用有限脉冲响应结构，则p阶滤波器的系数定义为

通过将输入信号与滤波器的脉冲响应作卷积估计所要信号，用向量表示为

其中输入信号向量

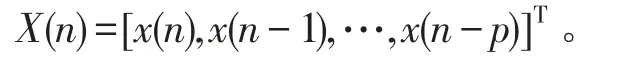
误差信号是所要信号与估计信号之差

滤波器根据滤波器系数的校正因子ΔWn自动调节滤波器系数

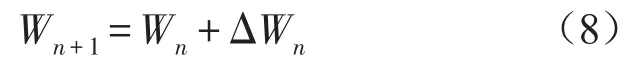
最小均方（LMS）自适应滤波器采用误差均方值的函数ΔWn=E[e2]作为校正因子，输入信号为实数则校正因子的表达式为

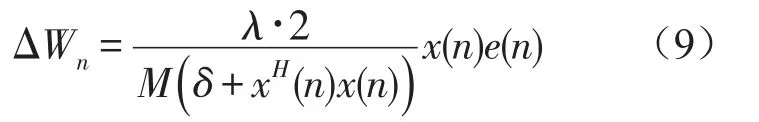
式中0＜λ≤1为权重因子，δ为方差修正因子，M为滤波器的阶数，最终通过迭代的方式得到滤波器的最优系数[8]。

利用自适应滤波方法对齿轮箱的振动信号进行滤波，得到信号的幅值谱如图6所示。图中a、b、c分别代表了原始信号幅值谱、参考信号幅值谱以及滤波后信号的幅值谱。从图中可以看出，参考信号中包含了原始信号中有用的频率成分，但幅值较小，经过自适应滤波后，提取了原始信号中与参考信号频率成分一致的有用成分，降低了信号中的噪声。滤波得到的信号在幅值上有所衰减，但满足故障诊断的要求。

图6 自适应滤波效果

3 在线振动数据研究

本文的验证数据来源于某风电机组齿轮箱的实时在线监测数据。故障后的数据采集日期为2013年10月15日，经开箱验证，齿轮箱高速轮齿存在划痕（如图7所示）；为了验证方法的有效性，提取了数据库中2013年4月14日采集的数据，作为故障前的数据进行对比。鉴于在齿轮箱不同部位在线振动信号采集数据的速率不同，需要将信号进行插值处理，将信号规整到统一的频率。插值方法采用三次样条方法，将信号规整到5 000 Hz，故障信号规整后的信号如图3所示。数据的计算步骤如下：

（1）将数据规整到统一的采样频率5 000 Hz；

（2）齿圈振动信号和低速轴振动信号分别与高速轴振动信号进行互相关运算，得到互相关信号c1，c2（分析故障信号得到的互相关信号时域波形如图3中a和b所示）；

（3）求互相关函数的和函数c=c1+c2（分析故障信号得到的和函数幅值谱如图6中b所示），并截取8192个数据点，以该数据为参考信号；

（4）进行高速轴振动信号的自适应滤波计算，求得滤波后的信号y（如图7～图8中b所示），然后进行故障判断。

图7 高速齿轮划痕损伤

图8和图9分别对应了故障前和故障后信号的处理结果，故障前后的振动信号经过空间自相关和自适应滤波，然后得到信号的幅值谱（原始信号最高采样率为2 500 Hz，进过插值规整后5 000 Hz以后，并不影响原来信号的频率成分，为了将信号图谱放大，故幅值谱中只显示了1 250 Hz以内的成分）。图中a分别代表原始信号的时域波形；b代表滤波后信号的时域波形；c代表原始信号的幅值谱；d代表滤波后信号的幅值谱。从图中看出，信号经过自适应滤波后幅值略有降低，但保留了信号中大部分的有用成分，降低了噪声对该部分的干扰，更加突出了转频（1X部分）及其倍频（2X、3X部分）等故障特征。因此，通过空间相关与自适应滤波对振动信号分析后，能够将信号中幅值较大，传播距离较远的特征信号从原始信号中提取出来，也就是振动的转频及其倍频部分，更加清晰的显示出来，进而通过振动转频及其倍频幅值的大小来判断是否存在故障。

4 结语

当齿轮箱存在故障时，就会产生较大的振动幅值，进而能够传播到较远的距离，而相关分析能够提取不同测点信号的相似成分。因此，本文提出了以空间相关法为参考信号的自适应滤波方法。通过对齿轮箱不同测点的振动信号进行互相关分析，得到了两个信号的相关成分，并以该成分为参考信号对高速轴测点的振动信号进行自适应滤波，提取了信号中的相似成分。利用幅值谱分析方法对滤波后信号进行分析，可以更加清晰的得到故障信号的转频及其倍频，利用转频及其倍频的变化有助于及时诊断齿轮箱存在的故障。方法的有效性也得到了现场实际测试数据的验证。

图8 故障信号自适应滤波的效果

图9 故障前信号自适应滤波的效果

[1]World Wind Energy Association.The world wind energy association 2013 half year report[M].Bonn：World Wind EnergyAssociation,2013.2-3.

[2]李俊峰.2012中国风电发展报告[M].北京：中国环境科学出版社，2012.75-77.

[3]Stefan Faulstich,Michael Durstewitz,et al.Germany wind energy report 2008[M].Kassel：Institute for Solar Energy Supply Technology,2008∶24-26.

[4]龙泉.风电机组齿轮传动系统动态特性及故障诊断方法研究[D].北京：华北电力大学，2012

[5]Z.Hameed,Y.S.Hong,et al.Condition monitoring and fault detection of wind turbines and related algorithms∶A review[J].Renewable&Sustainable Energy Reviews, 2009,13∶1-39.

[6]唐新安，谢志明.风力机齿轮箱故障诊断[J].噪声与振动控制，2007，1：120-124.

[7]王金福，李富才.机械故障诊断的信号处理方法：频域分析[J].噪声与振动控制，2013，1：173-180.

[8]雷亚国，何正嘉.行星齿轮箱故障诊断技术的研究进展[J].机械工程学报，2011，47(19)：59-67.

[9]B.Widrow.Adaptive noise cancelling∶principles and applications[J].Proceedings of the IEEE,1975,63∶1692-1716.

[10]J.Antoni,R.B.Randall.Unsupervised noise cancellation for vibration signals∶part I-evaluation of adaptive algorithms[J].MechanicalSystemsandSignal Processing,2004,18∶89-101.

[11]G.Ibrahim,A.Albarbar.Adaptive filtering based system forextractinggearboxconditionfeaturefromthe measured vibrations[J].Measurement,2013,46∶2029-2034.

[12]刘刚，杨全枝.冲击震动波在砂岩介质中传播规律的试验研究[J].工程勘察，2012，12：75-83.

[13]邵成华，姚善化.一种应用于自适应降噪的变步长LMS算法[J].噪声与振动控制，2007，4：110-111.

Gearbox Fault Diagnosis Based on Spatial Correlation andAdaptive Filtering

ZHOU Ji-wei

(Zhong Neng Power-Tech.Development Co.Ltd.,Beijing 100034,China)

∶The vibration signal is one of important bases for fault diagnosis of wind turbine gearbox.In this article,the correlation of vibration signals acquired from different positions of gearbox is analyzed,and the cross-correlation signal is obtained simultaneously.Then,the model of adaptive filtering by utilizing the cross-correlation signal as a reference signal is established,and the similar components of different vibration signals are extracted.Afterwards,the amplitude spectrum method is utilized to analyze the similar components,and the rotating frequency and its harmonics,which are significant for fault diagnosis of the gearbox,are obtained.Finally,the effectiveness of the method is verified by online vibration data.

∶vibration and wave;fault diagnosis;gearbox;correlation analysis;adaptive filter;vibration signal

TP206+.3；TN731；TN911.7< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.036

1006-1355(2014)06-0161-05

2014-03-06

周继威（1981-），男，河北廊坊人，工程师，主要研究方向：风电场设备状态监测技术研究。

E-mail∶zhoujiwei@clypg.com.cn