IWO与BPNN混合智能算法在转子故障诊断中的应用

孟昭燃，赵荣珍

（1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室，兰州730050；2.兰州理工大学 机电工程学院，兰州730050）

IWO与BPNN混合智能算法在转子故障诊断中的应用

孟昭燃1，2，赵荣珍1，2

（1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室，兰州730050；2.兰州理工大学 机电工程学院，兰州730050）

在经典IWO杂草算法的基础上提出一种适用于神经网络优化的新算法。该算法将多种结构的神经网络权值阈值编码为不同维度的杂草种子，以神经网络均方误差作为种子适应度的统一评价标准，同时对多个维度的杂草种子进行排序筛选，实现了神经网络权值阈值与结构同时优化的目的。应用该方法于转子系统故障分类问题，实验结果表明该方法可以在结合BP算法优势的同时有效优化神经网络各参数，可以得到分类精度高、结构最简且泛化能力强的神经网络故障分类器。

振动与波；杂草算法；神经网络；智能优化；故障诊断

过去十余年，人工神经网络得到了良好发展，在各领域中解决了大量间序列预测、分类、聚类及回归等问题[1—3]。故障诊断技术的实质是模式识别问题，即在故障特征信号与故障类型间建立映射[4]。而故障特征信号常难以用数学规则描述，且设备常难以建立精确的数学模型，这种情况下，人工神经网络以其成熟的理论背景与强大的非线性映射能力成为机械设备故障诊断的重要方法[5]。人工神经网络学习能力和泛化能力是判断其是否能在工程中应用的关键，这些能力是由神经网络的权值与结构直接决定的。目前多用基于误差梯度信息反向传播法计算神经网络权值，这一类方法应用广泛，但也存在一些缺陷。

粒子群算法PSO与遗传算法GA等一类智能数值优化算法可以通过寻找全局最优来优化神经网络，使其获取最佳的权值与结构[6,7]。近年，IWO（Invasive Weed Optimization）杂草算法又作为一种新的仿生智能数值优化算法解决了大量工程优化问题[8]。杂草算法由Mehrabian与Lucas于2006年提出，并利用该算法求解3个标准多维数值优化函数集及解决了1个鲁棒控制器优化与调节问题验证算法性能[9]；2010年张氢等利用马尔科夫链证明了IWO算法的全局收敛性，同时用一个齿轮箱优化实例对其观点进行验证[10]。杂草算法已然在多个领域崭露头角，而将改进IWO用于神经网络故障分类的研究尚未见相关报导。

本文将介绍这一新兴优化算法并提出更适合神经网络故障诊断的改进，讨论适用于神经网络优化的参数设置问题。结合杂草算法与BP算法将网络权值与结构同时进行编码处理代入算法进行优化，试图增强网络的学习能力的同时保证其泛化能力，使其在旋转机械故障诊断中得到更小的故障特征分类误差并且更具实用性。

1 神经网络

神经网络是相互连接的神经元的集合，这些神经元可以通过学习从复杂的数据中发现本质的线性和非线性的趋势。其结构由一个输入层、一个隐含层和一个输出层构成，每一层包含若干神经元，各层之间通过不同的权值和阈值相连。各层关系如图1所示[11]。

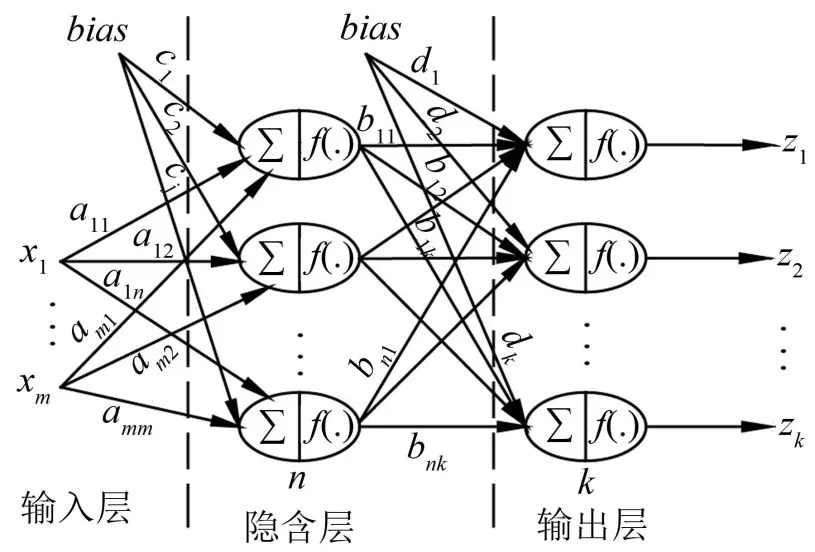
图1 神经网络模型

其中，权值决定神经元强度，阈值确定神经元对数据分类的界限。激励函数常由S型函数（Sigmoid）充当，数学形式如式(1)

这一函数输出范围为0与1之间的闭区间，并且连续可微，于是可以使用BP(Back Propagation)方法作为网络的学习方法，即通过误差梯度的修正实现网络权值的逐步调整。BP法已被证明是一种优秀的局部搜索方法，然而BP法对网络的初始权重非常敏感，当初始权重不同必然会收敛于不同的局部最小。随机初始化的网络每次训练都会有不同的结果，导致无法确定最优网络。三层BP网络已经被证明可以拟合任意的非线性关系。但对于隐含层节点数的取值，一直没有出现有说服力的方法。杂草算法可以为这些问题提供解决思路。

2 IWO算法

2.1 算法原理

模拟自然界中杂草占领生存空间生长繁殖的特性进行寻优计算的IWO算法与遗传算法、粒子群算法等相似，都是一种与群体智能相关的计算方法[12]。算法可以用如下伪代码表示：

(1)随机初始种群；

(2)依据调制指数确定最初与最终的标准差σ；(3)重复下列步骤：

①计算植株适应度值并排序；

②根据适应度繁衍子代；

③达到最大种群数目，父子代竞争；

(4)达到最大迭代次数，算法停止。

计算杂草种子数目的函数如式（2）

其中x指植株的适应度，C为适应度最大值，D为适应度最小值，floor地板函数实现向下取整，这一关系可由图2表示。

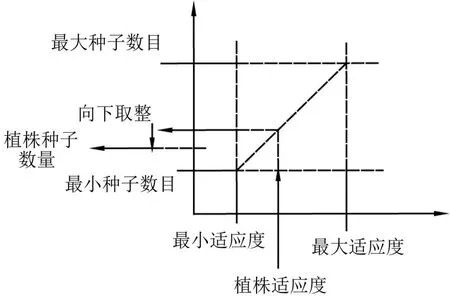
图2 杂草种子数计算方法

每代种子在解空间中的位置与父本相关，父本与子代间的距离符合均值 μ为0。每代标准差σiter随迭代次数非线性减小的正态分布，用式（3）计算。

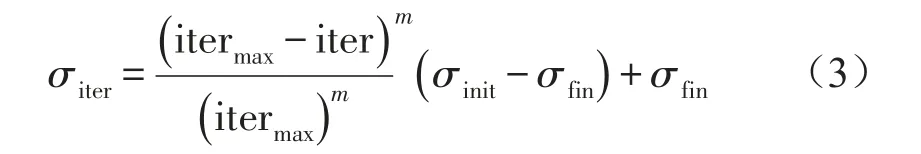
itermax是初始化时设定的总迭代次数，m为非线性的调制因子，σinit和σfin是需要根据解空间设定的最初与最终标准差。带有非线性系数m的项使得适应值好的个体聚集，种群缓慢地由向外扩张转向内部斗争。

杂草算法的思想确保了每个初始解都有生存的可能使算法可以全局搜索，同时，利用可行解的优势保证算法的局部搜索能力。

3 改进杂草算法优化神经网络

针对神经网络优化中的具体问题，在具体分析杂草算法搜索过程之后，从杂草算法资源占用，神经网络参数编码，杂草种子的适应度计算三个角度进行了讨论，最后给出杂草算法优化神经网络流程。

3.1 算法原理

经典的杂草算法在解决高维问题时非常出色，神经网络有大量参数，是典型的高维寻优的问题。经典的杂草算法中，种子需要相同的维度，限制了算法只能在相同网络结构下优化初始权值。根据杂草算法的思想本文进行了若干改进。

首先是算法初始化时的改进。在算法开始时投入不同维度的种子，分别计算其解空间的适应度后统一排序，即令不同种类的杂草在同一区域竞争，长期处于劣势的种群会自然消失。

其次对基本步长σ变化方式做出改进，引入一个与迭代次数相关的周期函数。改进后的杂草算法种子分布标准差算式如式（4）

cos因子的加入使IWO算法可以让算法更快找到最优值，节省资源并且保持了不易早熟的特点，也体现了杂草按簇生长的自然规律。同时将算法允许的最小种子数设为0，放弃适应度最低的植株，二者结合可有效减少算法的运算步骤，减小初始化时的改进带来的计算压力。

图3中平滑下降的是经典IWO算法标准差变化曲线，震荡下降的是改进后的杂草算法，改进使得算法标准差变化灵活，在搜索中做更多尝试。

3.2 杂草种子编码

神经网络进输入层节点数m取决于分类信号的特征维数，输出层节点数n为需要分类的类别数目，隐层节点数n由杂草算法确定。如图1所示，权值aij和阈值cj存在于输入层与隐层之间，bij与dj在隐层与输出层之间。为将权值aij、bij和阈值cj、、dj同时进行优化，把它们编码成一个行向量作为种子，种子初始化时每一维都规定在（-1，1）之间，则每颗种子就是神经网络的一种初始化方案，其维度计算方法如式（5）

图3 杂草算法标准差变化对比

权值占用每颗种子m×n+n×k个维度，阈值占用n+k个维度。不确定的变量n会造成种子维度不一致。IWO算法中子代由父代直接播种，子代植株的维度仅与其父代相关，将不同维度的解决方案编码为不同维度的初始种子同用神经网络MSE决定其繁殖能力，实现不同结构网络之间的比较，保持神经网络学习的整体性。

3.3 适应度计算

网络分类的均方误差MSE做杂草算法适应度引导算法进行搜索，MSE计算公式如式（6）

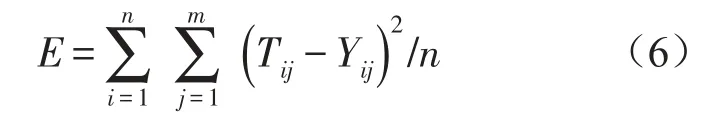
式中Tij是期望输出值；Yij是实际输出值；m是输出节点数；n是训练样本数。因为网络得到的MSE估计在10-10～102之间，取其负对数-log E作为适应度方便式2进行种子数目计算。网络训练时用一部分数据作为验证集，当前神经网络对验证集分类，6次迭代误差曲线不下降则停止自动网络训练，得到该方案的适应度值。

3.4 算法流程

图4 算法流程

4 仿真实例

采用转子试验台模拟并测量了3 000 r/min下转子系统正常状态和不平衡、支座松动、不对中、碰磨四种常见故障的振动信号，采用12个传感器采集，通过对振动信号进行分段处理，得到每种状态下的120组样本。经滤波和消噪后计算这12个传感器测得振动信号的均值、标准差、峰值、峰峰值、方根幅值、均方根值以及无量纲指标峭度、偏度、裕度、峰值指标、波形指标11种特征特征值。为使神经网络不至于过大，利用PCA(Principal Component Analysis)方法进行筛选，最终选取每组样本的6个可以敏感反应设备状态的特征归一化后作为网络输入，筛选详细过程见文献[13]。将这120组5种样本随机划分为三份，即每份40×5组，分别用来训练网络，检查网络收敛情况和测试网络性能。划分时用的随机抽取方式，可以保证数据的典型性。网络输出z为一个5位二进制数，每一种状态对应某一位取1其余为0，如正常状态对应图1中的输出为z1取值1，z2到z5为0，即{1 0 0 0 0}。

图5 转子试验台

根据选定的故障特征与对应的运行状态，构造输入层节点数为6，输出层节点数为5的神经网络，其隐层节点数根据多种经验公式进行估计后定位于2—9之间，由式(4)计算得种子的维度为12n+5。参照Mehrabian等在文献[9]中给出的建议，根据神经网络的参数与精度要求设置杂草算法参数设置如表1。

图6显示了算法运行200代适应度的变化，可以看出最小适应度在160代附近即不再变化，此时网络精度已达到10-6。算法构造的神经网络由4个隐含节点构成，提取杂草算法计算出的网络参数，重新训练网络得到的MSE变化如图7。

图6 每代杂草神经网络均方误差

表1 算法参数设置

图7 杂草优化的神经网络均方误差变化

图7中曲线表示优化后网络重新训练时均方误差变化，曲线平滑，稳定下降，经过34次迭代停止变化，误差为2.481 9×10-6，说明优化后的网络能在保证误差极小的情况下快速收敛。

图8显示了网络输出与目标输出的对比。1～5依次代表正常、不平衡、支座松动、不对中、碰磨5种状态，每格中加粗数字为网络输出的样本数目，表示网络将多少个样本判定为这一状态，下方百分比为实际输出的样本数在总样本数中所占比例；第6行

图8 杂草神经网络分类误差

统计了实际输出的正确率和错误率，第6列是目标输出样本数的统计值。当出现误判，该图可以清晰定位误判类型和显示错误比例，例如若网络将5个状态3的样本错误的输出为状态1，则样本数5会出现在第1列第3行，便于分析误判原因。

图8中网络得到了100%的分类正确率，网络对其训练数据集做到了完美拟合，对3 000 r/min的设备状态做到准确分类。分类结果表明改进的IWO算法运行200代后能在得到很小的网络结构同时保证网络的拟合能力与泛化能力。

5 结语

本文为寻找神经网络权值阈值与结构的最优解，通过调整IWO种子产生方式与每代标准差变化方式对算法进行了改进，多维度的种子对不定确定维度的问题进行优化，用标准差震荡变化减小算法的运算量。改进后的IWO算法保持了经典IWO强大的非线性快速搜索能力，优化的神经网络性能优秀，可以满足故障诊断的需要，展示了这一混合智能算法在工程应用方面潜在的巨大能力，也为其他变维度非线性优化问题提供了解决思路。

[1]赵荣珍，张优云.基于数据挖掘和机器学习的诊断智能研究[J].振动工程学报，2004，17(z1).

[2]栾美洁，许飞云，贾民平.旋转机械故障诊断的神经网络方法研究[J].噪声与振动控制，2008，28(1)：85-88.

[3]雷亚国，何正嘉，訾艳阳.基于混合智能新模型的故障诊断[J].机械工程学报，2008，44(7)：112-117.

[4]何正嘉.机械故障诊断理论及应用[M].北京：高等教育出版社，2010.

[5]张新海，雷勇.BP神经网络在机械故障诊断中的应用[J].噪声与振动控制，2008，28(5)：95-97.

[6]刘芬，潘宏侠.WCPSO优化的小波神经网络在传动箱故障诊断中的应用[J].噪声与振动控制，2011，31(5)：146-149.

[7]易建钢，陈奎生.集成动态神经网络及其在冶金风机智能诊断系统中的应用[J].噪声与振动控制，2007，27(5)：97-99.

[8]SU S-b,WANG J-w,ZHANG L等.An invasive weed optimization algorithm for constrained engineering design problems[J].中国科技大学学报,2009,39(8)∶885-893.

[9]Mehrabian A R,Lucas C.A novel numerical optimization algorithm inspired from weed colonization[J].Ecological Informatics,2006,1(4)∶355-366.

[10]张氢，陈丹丹，秦仙蓉，等.杂草算法收敛性分析及其在工程中的应用[J].同济大学学报，自然科学版，2010，38 (11)：1689-1693.

[11]Samarasinghe S.Neural networks for applied sciences and engineering∶fromfundamentals to complex pattern recognition[M].CRC Press,2006.

[12]彭斌，胡常安，邵兵，等.求解TSP问题的混合杂草优化算法[J].振动、测试与诊断，2013，33(z1).

[13]张涛.转子故障数据CRFS分类方法研究与测试系统开发[D].兰州：兰州理工大学，2013.

Application of Hybrid IntelligentAlgorithm of Invasive Weed OptimizationandNeuralNetworkinRotorSystemFaultDiagnosis

MENG Zhao-ran,ZHAO Rong-zhen

(1.Key Laboratory of Digital Manufacturing Technology andApplication, The Ministry of Education Lanzhou,Lanzhou 730050,China; 2.School of Mechanical and Electronical Engineering of Lanzhou Univ.of Tech.,Lanzhou 730050,China)

∶Based on the classical ecologically inspired meta-heuristic Invasive Weed Optimization(IWO)algorithm,a hybrid intelligent algorithm is proposed.In this method,the weights and thresholds of multi-structures of the neural network are coded as weed seeds with different dimensions,and the MSE of the neural network is used as the uniform index for evaluation of the fitness of the weed seeds.The weed seeds with multi-dimensions are then arranged and optimized.The simultaneous optimization of the weights,thresholds and the structure of the neural network are realized.Then,this algorithm is applied to the fault classification of rotor systems.Results of the experiment show that this new method can reserve the advantages of the BP algorithm while optimizing the neural network parameters,and obtain a fault classifier for the neural network with high accuracy,simple structure and strong generalization ability.

∶vibration and wave;invasive weed optimization(IWO);neural network;intelligent optimization;fault diagnosis

TP18；TH165< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.034

1006-1355(2014)06-0153-04+160

2013-12-27

国家自然科学基金项目（51165019）；

国家自然科学基金项目（50875118）

孟昭燃（1989-），男，山东泰安人，硕士生，主要研究方向：机械故障诊断。

赵荣珍，女，博士生导师。

E-mail∶348316553@qq.com