计及电动汽车充电调度可行域的电力系统机组最优组合

陈 彬，王业磊，许 昭，文福拴

(1.福建省电力有限公司 电力科学研究院，福建 福州350007;2.浙江大学 电气工程学院，浙江 杭州310027;3.香港理工大学 电机工程系，香港 九龙999077)

0 引 言

电动汽车作为解决交通、环境和能源问题的重要措施，近年来在国际上逐步受到重视，在北美、欧洲等国家已经形成了规模市场［1，2］。大量可入网电动汽车(plug-in electric vehicle，PEV)的无序充电会给电力系统安全与经济运行带来严重负面影响，这样如何优化调度电动汽车充电就是值得研究的重要问题［3］。

到目前为止，针对电动汽车的充放电调度问题，国内外已经做了一些研究工作。文献［4］以配电系统网损与电压偏移最小化为目标建立了电动汽车最优充电策略模型，考虑了负荷预测的不确定性与支路潮流约束。文献［5］研究了有电动汽车充放电负荷时的电力系统概率潮流问题。文献［6］以丹麦电力市场为背景，研究了电动汽车的最优调度模型，以考虑了充电成本、电池折旧成本、燃油成本在内的电动汽车总运行成本最小为目标。文献［7］研究了电动汽车广泛接入电力系统后的机组最优组合问题，综合考虑了发电机组运行成本最小和CO2排放量最小这两个目标，并采用分段线性化方法将机组最优组合问题转化为混合整数规划问题进行求解。文献［8］应用蒙特卡罗仿真法研究了电动汽车充放电行为的统计特性，发展了以最小化系统总发电成本期望值为目标的随机经济调度模型，并采用内点法求解，但研究工作仅限于单时段优化调度且并未考虑网络约束。文献［9］在［8］的基础上，将单时段经济调度问题发展到多时段的优化调度问题，并计及了网络安全约束，发展了能够容纳PEV 的电力系统优化调度的数学模型，兼顾了PEV 车主的经济效益和发电的碳排放成本。

综上所述，现有电动汽车充电优化调度方面的研究工作尚未很好地统筹考虑电动汽车用户的出行需要和充电能量需求。有必要研究考虑PEV用户自身需求的、容纳充电能量需求的电力系统优化调度，这与智能电网环境下倡导用户的主动性相适应［10～12］。基于这样的考虑，本文研究计及电动汽车用户行车需要和充电能量需求的电力系统机组最优组合问题。

未来电动汽车参与系统调度的一种可能的模式为:车主以限时能量合约把电动汽车停车时段的充电业务通过充电代理机构交付给调度机构，充电代理承诺在指定时段内给电动汽车充入约定的电能，调度机构则通过充电代理机构实现对电动汽车的充电调度。本文下面所研究的电动汽车调度问题以这种模式为基础。考虑到电动汽车向电力系统反向送电尚存在技术、政策、量测和商业模式等多方面的问题，本文的研究局限于电动汽车充电问题。

1 电动汽车充电调度的可行域分析

1.1 对单车单次充电调度的可行域分析

电动汽车用户的充电需求可用停车时间段Ttot和所需充电电能Eneed这两个指标来描述，即用户希望在停车的Ttot时间段内充入Eneed的电能。假定Pmax是此电动汽车充电功率上限，则满足充电需求所需最少充电时间为

电动汽车在此时段内能保持不充电的最长时间为

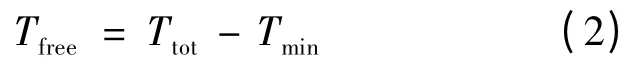
电动汽车在充电过程的实时功率会按调度指令在0 到Pmax之间变化，累积充电能量的变化在0 到Eneed之间。不过，0 和Eneed并不是充电时段中每个时刻的下确界和上确界。下面分析尽早充电模式(即在可充电的时间段内尽早完成充电的模式)和最晚充电模式(即在可充电的时间段内尽可能在时段结束时完成充电的模式)这两种极端情形下的累积充电能量的上下界，其他充电模式介于这两个模式之间。

(1)尽早充电模式

尽早充电模式指尽可能快地满足用户充电能量需求，即在开始的Tmin时间段里保持最大充电功率Pmax直到完成用户设定的充电能量Eneed为止。在随后的Tfree时间段内，电动汽车和电力系统无能量交换行为。

(2)最晚充电模式

与尽早充电相反，最晚充电模式则尽可能延迟用户的充电能量需求。在前Tfree的时间段内，不对电动汽车充电，在最后的Tmin时间段内以最大充电功率Pmax进行充电，在时段结束时，电动汽车累积充电能量正好满足用户需求。

这里给出一个例子。某用户决定在5 h 内为电动汽车充入2 kW·h 电能，其电动汽车最大充电功率为2 kW，则上述两种充电模式下电动汽车充电功率曲线如图1 所示。

图1 所对应的累积充电能量曲线，即充电功率曲线对时间的积分，如图2 所示。

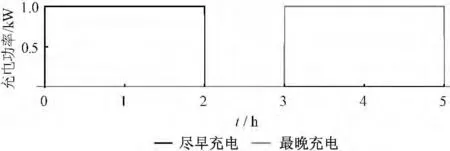
图1 电动汽车在两种充电模式下的充电功率Fig.1 PEV charging power curves under two charging modes

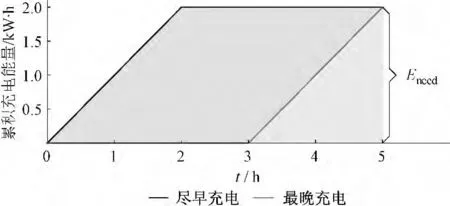
图2 电动汽车在两种充电模式下的累积充电能量Fig.2 PEV cumulative charging energy curves under two charge modes

从图2 可以看出，采用这两种极端充电模式的电动汽车累积充电能量曲线都是起点为(0 h，0 kW·h)、终点为(5 h，2 kW·h)的曲线。这两种极端充电模式确定了累积充电能量曲线的上确界和下确界，因为任意一种充电模式对应的累积充电能量不可能大于从一开始就以最大功率充电的尽早充电模式，而其累积充电能量曲线如果有一部分位于最晚充电模式曲线的下方，则不可能在时段结束时满足电动汽车用户的能量要求。所以，此上下界间的区域即为电动汽车累积充电能量曲线的可行域。设采用尽早充电模式和最晚充电模式时在时刻t 的充电功率分别为Pup(t)和Plow(t)，则该时刻的电动汽车充电功率P(t)需满足式(3)和(4)所描述的约束:

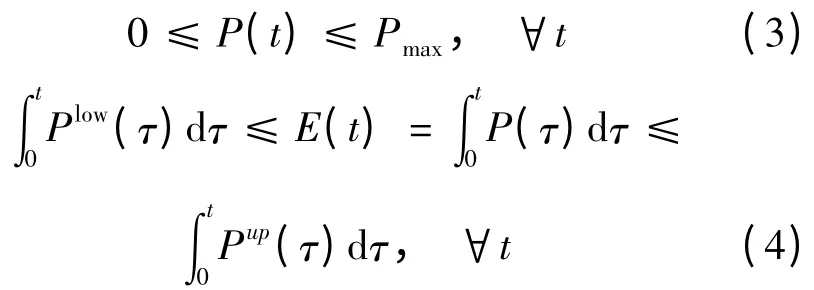
式(3)和(4)分别为电动汽车充电过程中的充电功率约束和累积充电能量约束。在现有的考虑可入网电动汽车的系统调度模型中一般只考虑了充电功率约束式(3)，而未包括真正能反映电动汽车充电能量需求的累积充电能量约束式(4)。

从图2 可以看出，在电动汽车充电过程中，两曲线围成的平行四边形面积越大，其充电调度的灵活性越大。设采用尽早充电模式和最晚充电模式时时刻t 的累积充电能量分别为Eup(t)和Elow(t)，则可用下式描述电动汽车充电灵活性:

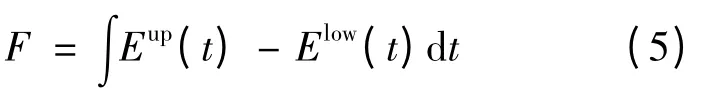
式中:F 为描述充电灵活性的指标。

对于单车单次充电情况，式(5)可变换成如式(6):

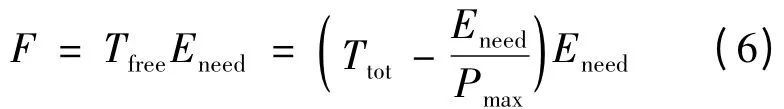
由式(6)可以看出，F 随总充电时间Ttot和最大充电功率Pmax的增大而增大。F 是充电需求能量的一个二次函数;需求能量取中间值即Eneed=时充电灵活性最大，取最大值TtotPmax和最小值0 时的充电灵活性最小，此时F 均为0。充电需求能量最大意味着充电功率始终为最大值，其为0 则意味着充电功率始终为0，这两种极端情况均无充电灵活性可言。

1.2 对大量电动汽车充电调度的可行域分析

基于前文对单车单次充电行为的分析，这里研究有大量电动汽车充电时的调度可行域，这需要计及用户日常开车出行习惯和相关的充电能量需求。这里以丹麦的国家交通调查结果中的工作日行车数据为基础进行分析。该调查结果中提供了十万多个拥有家庭汽车的用户在某一天的具体行车记录，包括每次出行的开始时间、结束时间、行驶里程等详细内容，文献［13］对这些数据做了一些统计分析。这里基于该调查数据并做了一些假设，对有大量电动汽车情形下的充电调度可行域进行定量模拟和分析。

假定电动汽车车主每次停车时间大于2 h 时，就会选择跟充电代理签订限时充电合约，合约时间为当次停车时间，合约能量则取为能满足当日后续出行要求所需最低能量并加上一定的裕度。对于合约结束时段为次日早晨的夜间长时间停车，合约能量则可为充满电池所需电能。电动汽车相关参数设定见表1。

表1 电动汽车相关参数设定值Tab.1 Settings of PEV parameters

基于丹麦的国家交通调查结果数据和如上假设，用前述的求取累积充电能量上下界的方法求取每个电动汽车用户的累积充电能量上下界并进行汇总，即可得到电动汽车总充电功率P(t)和总累积充电能量E(t)的约束方程式:

式中:Nv表示电动汽车总数;Ik(t)为随时间t 变化的0 ～1 变量，表示第k 辆电动汽车在t 时刻是否并网(0 和1 分别表示不并网和并网);Elowk(t)和Eupk(t)分别为第k 辆电动汽车的累积充电能量下界和上界。对一万辆家庭电动汽车在工作日期间行车与充电行为进行模拟可得到式 (7)和(8)所表示约束的数值结果参见附录A (略)，图3 和图4 分别为与之相应的各时段总充电功率上界和总累积充电能量上下界。

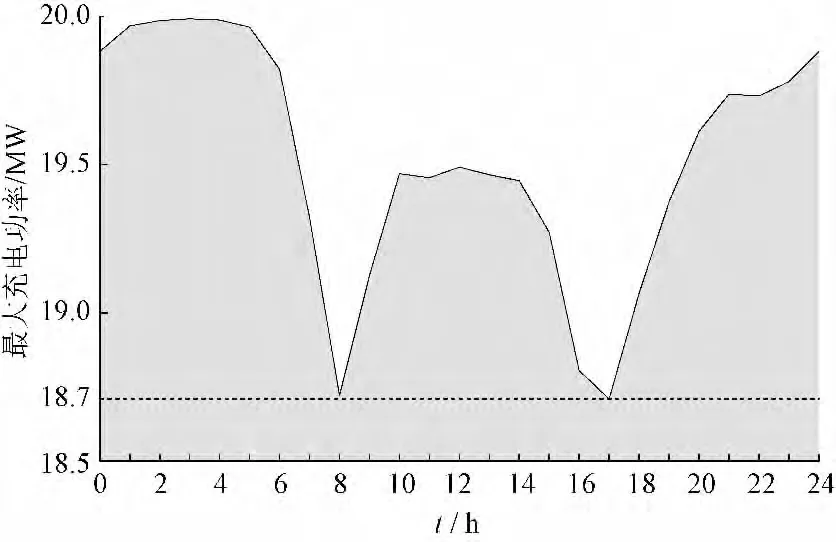
图3 10 000 辆电动汽车在工作日各时段总充电功率上界Fig.3 The maximum possible PEV charging power of 10 000 PEVs in different hours of a working day

从图3 可以看出，因为一天之内绝大多数电动汽车处于停泊状态，所以每个时段电动汽车总充电功率的峰值非常大。从图4 中可以看出，每万辆电动汽车一天平均需要充电约36 MW·h，即平均每辆电动汽车需要补充24 km 所需电能;另外可以看出，在早晨7 ∶ 00 至8 ∶ 00 和晚上17∶ 00至18∶ 00 时段，因为大量电动汽车需要在这两个时段提供通勤服务而无法充电，这反映到总累积充电曲线上就是在这两个时段累积充电能量下界突然提高，可行域出现瓶颈，电动汽车充电的灵活性下降。文献［13］的分析结果表明，在工作日期间电动汽车的行车规律相当稳定，此数值结果可作为确定量加入到最终的充电优化调度模型之中。

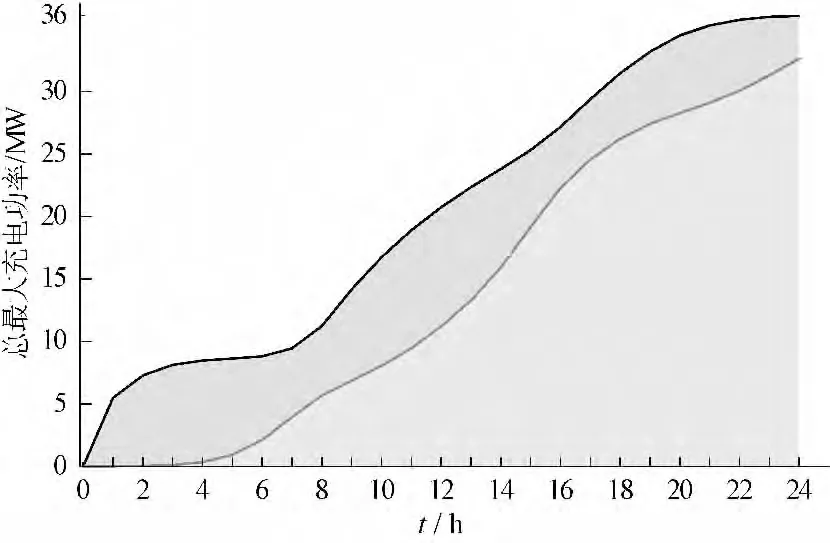
图4 10 000 辆电动汽车工作日的总累积充电能量上下界Fig.4 The upper bound and lower bound of aggregated PEV cumulative charging energy of 10 000 PEVs in different hours of a working day

1.3 充电功率分解

当调度机构获得所有电动汽车的总充电功率约束和总累积充电能量约束数据后，即可对电动汽车各时段充电功率进行优化调度，但充电代理需要把充电功率调度结果分解到每辆电动汽车。这里给出一种简单的分解方法。

累积充电能量曲线的上下界之间的区域是由各个电动汽车的单独累积充电能量上下界汇总而成，即因此可将调度机构得到的总累积充电能量曲线E(t)大于Elow(t)的部分以Eupk(t)－ Elowk(t)为权重进行分解，即电动汽车k 的累积充电能量曲线Ek(t)为

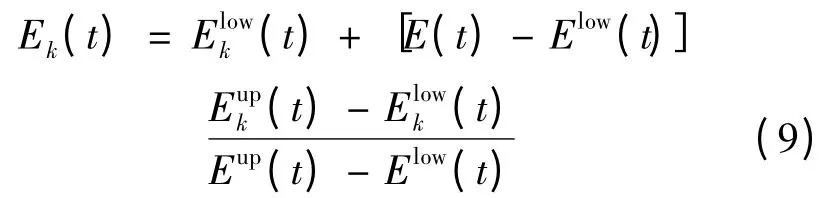
可以看出，由式(9)得到的Ek(t)在任何时段均处于和之间，满足累积充电能量约束。根据Ek(t)求取对应的Pk(t)，即可得到每个调度时段每辆电动汽车的充电功率。

2 计及PEV 的电力系统机组最优组合模型

计及PEV 的电力系统机组最优组合问题可以在传统的机组最优组合模型的基础上扩展，最终形成的数学模型如式(10 ～26)所示。这些公式中的小写字母表示决策变量、大写字母表示已知参数;i 表示发电机组编号，取值为1 至NG;τ 和t均表示时间段编号，取值为1 ～NT。相关符号说明见附录B (略)。

所发展的机组最优组合模型以给定时段内的发电燃料成本和机组启动成本之和最小为目标。

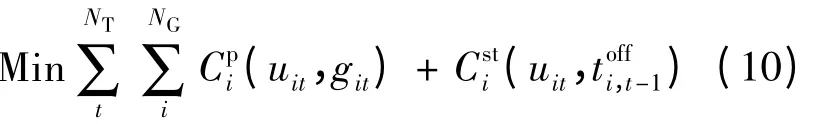
式 (10)中的发电燃料成本一般采用式(11)中所示的二次函数形式;机组启动成本则如式(12)所示，包括了冷热两种状态。

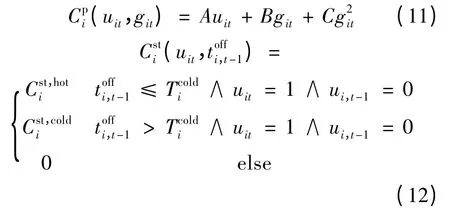
式(11，12)均不是线性函数。为便于求解，可以采用文献［14］的方法对式(11)做分段线性化处理;把式 (12)改用式 (13)和(14)描述。

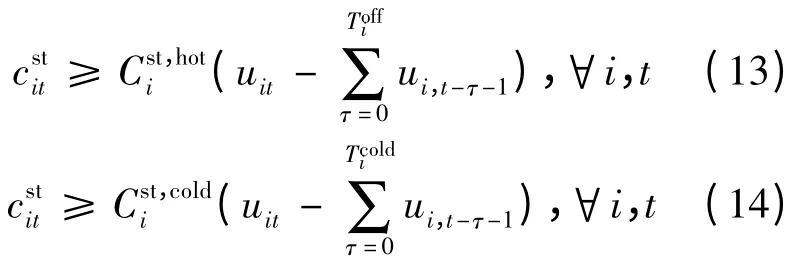
通过式(13，14)所描述的线性约束可确定各机组在各时段启动成本的下界。由于是以最小化目标函数为目标，在最优解处一般满足cstit=

需要满足的约束调节如下:

(1)功率平衡约束

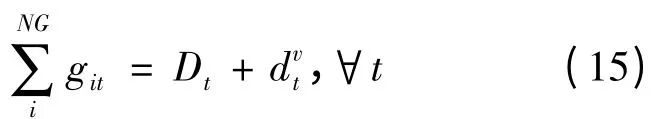
式(16，17)分别表示系统的上调和下调旋转备用需求。可以通过控制电动汽车减少总充电功率和增加总充电功率这两种方式来分别为系统提供上调和下调旋转备用。

(3)发电机组出力和爬坡约束

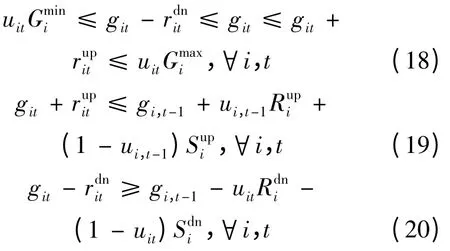
式(18 ～20)为同时考虑机组正常运行阶段和启停机阶段的爬坡约束。

(4)发电机组最小开停机时间约束为

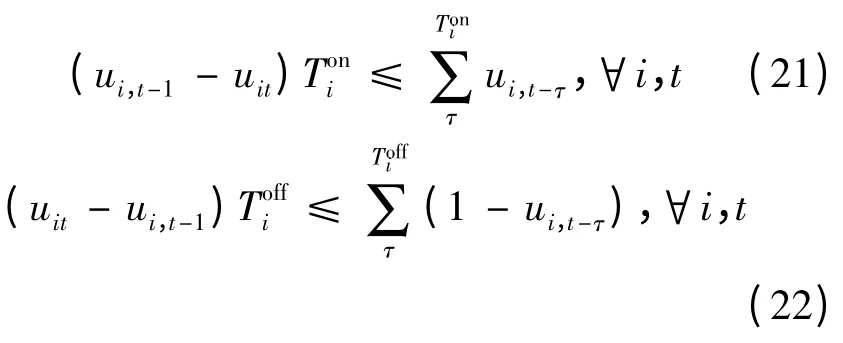
前已述及，在电动汽车调度方面需要满足车主出行需要和充电能量需求，可描述如下。

(5)电动汽车总充电功率约束

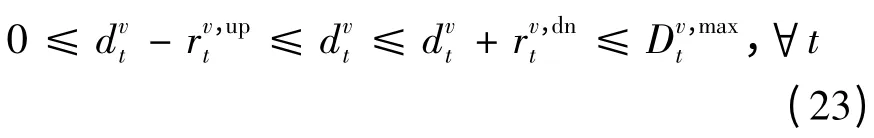
(6)电动汽车总累积充电能量约束

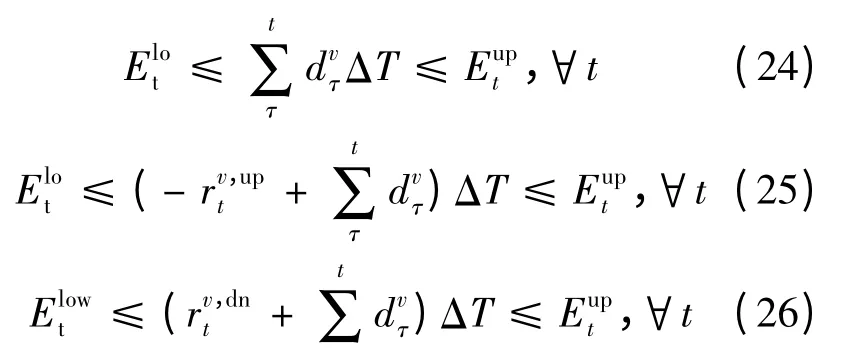
式(24 ～26)即为上一节所描述的电动汽车总累积充电能量约束的离散表达形式，式中ΔT为时段，本文取ΔT 为1 h。

经过上述处理后，所构造的优化模型的目标函数和约束都是线性的，整体上是混合整数线性规划模型 (Mixed Integer Linear Programming，MILP)，可选用现有的成熟商业软件求解。本文采用Gurobi 5.02 求解器求解该MILP 模型，运行环境为搭载4 核2.13 GHz CPU，2G 内存的个人电脑。

3 算例与分析

3.1 算例

采用文献［15］中的10 机系统来说明所构建的模型，相关参数列于附录C (略)。假定:(1)系统的上下调旋转备用水平均为当前负荷预测值的10 %;(2)电动汽车在电力系统中能量渗透率为10 %，即每天负荷消耗的总电能的10 %用于电动汽车充电，据此可估算出约有35 万辆电动汽车，如果所有汽车同时以最大功率进行充电的话，其充电功率可高达700 MW。

为分析PEV 负荷对电力系统运行的影响，有必要比较有与没有PEV 负荷时的电力系统机组最优组合的结果。为了进行合理的比较，这里对无PEV 负荷的情况设置如下:对于无PEV 的情形，为保持系统总负荷水平与有PEV 情形下相同，把每个时段的负荷设置为原负荷的1/ (1-10 %) =1.111 1倍。

3.2 计算结果

表2 和表3 分别列出了无PEV 和有PEV 时的机组最优组合结果。

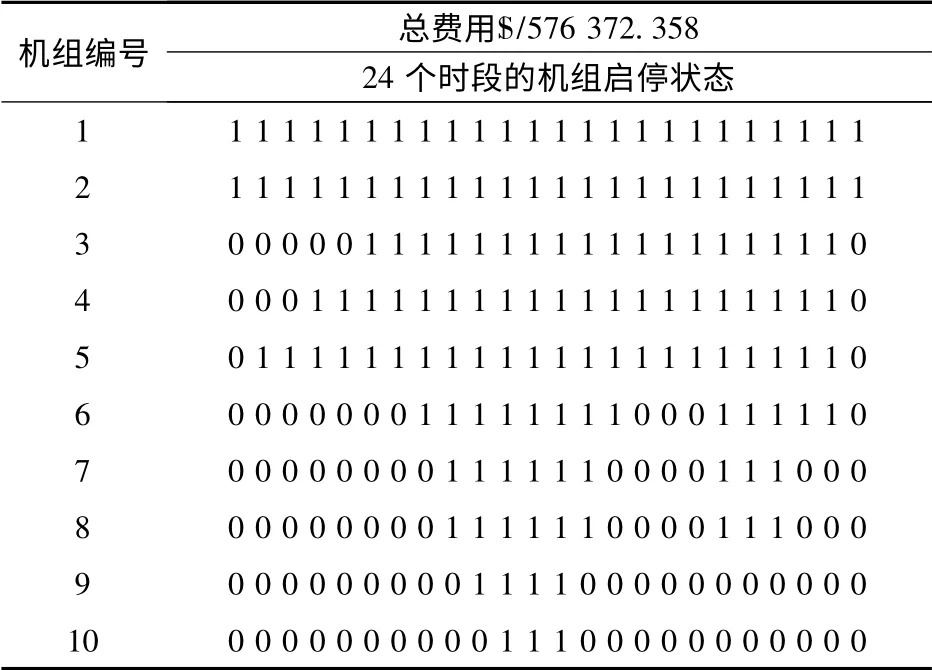
表2 无电动汽车时的机组最优组合Tab.2 Unit commitment for the scenario without PEVs

表3 有电动汽车时的机组最优组合Tab.3 Unit commitment for the scenario with PEVs

图5 显示了电动汽车充电调度对机组最优组合方案的影响。各时段的电动汽车总充电功率和包含电动汽车充电功率在内的总负荷曲线如图6 所示。

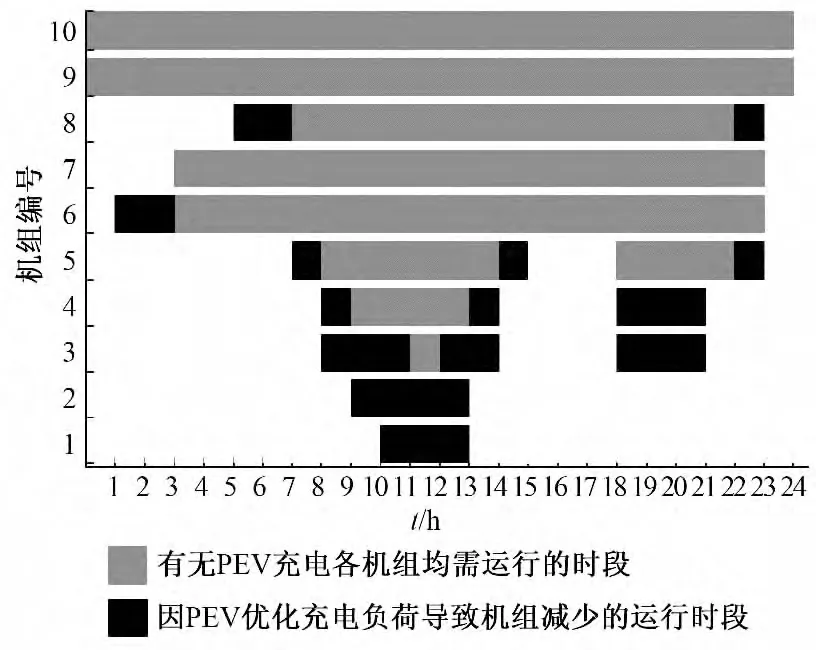
图5 PEV 充电对机组最优组合的影响Fig.5 Impacts of PEV charging on unit commitment

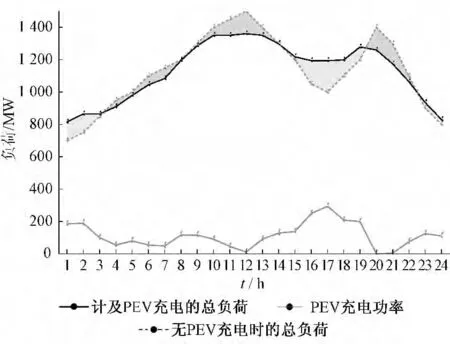
图6 有无PEV 充电负荷时的系统负荷曲线Fig.6 Load curves in the scenarios with and without PEV charging loads

由表2 和表3 可以看出，在总负荷水平维持不变的情况下，通过优化调度电动汽车使系统每天运行总成本减少了21 676S| ，下降了3 %。这是由于与无PEV 的情形相比，虽然有PEV 充电负荷时每日电能消耗量相同，但PEV 的优化充电调度使得负荷曲线发生了变化。从图5 和图6 可以看出，在优化调度电动汽车充电后，系统负荷曲线得到了优化，一些发电机组启停次数和运行时间有所减少，这降低了系统运行成本，改善了系统运行的经济性。另外，从图6 中可以看出，优化调度后的电动汽车在系统的两个用电高峰时段均停止充电(中午12 时和晚上20 时)，而在系统负荷低谷时段则有较大的充电功率。充电功率最大值294 MW出现在下午17 时，远低于其最大可能的充电功率700 MW。在部分时段虽然系统负荷处于较高水平但仍有电动汽车在充电，这是因为仍需满足部分车主在这个时段的充电需求。

从图7 可以看出，电动汽车累积充电能量于早晨6 时至7 时达到上界，于下午15 时至16 时达到下界。这说明在下午15 时前，由于系统总负荷处于高峰时段，电动汽车并未充入足够电能，累积充电能量曲线达到了下界。

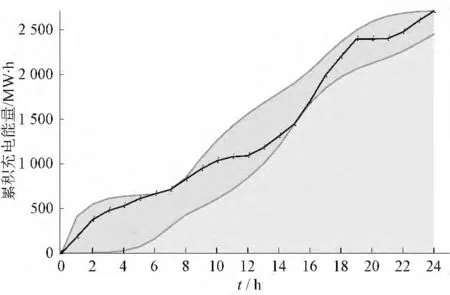
图7 电动汽车累积充电能量优化调度结果Fig.7 Cumulative charging energy under optimal charging dispatching of PEVs

4 结 论

本文首先分析了电动汽车用户出行需要和充电能量需求，提出了电动汽车充电调度可行域概念。之后，在传统的机组最优组合模型中引入了与电动汽车相关的约束，即综合考虑了电力系统运行约束、电动汽车用户出行需要和充电能量需求，发展了一种新的机组最优组合模型。最后，用算例说明了所提方法的可行性与有效性，并通过与没有电动汽车负荷时的机组最优组合结果比较，表明了对电动汽车优化调度可以改善电力系统运行性能。

(因篇幅所限，这里不给出附录A ～D，读者需要时可以发送电子邮件联系第二作者索取。)

［1］张文亮，武斌，李武峰，等.我国纯电动汽车的发展方向及能源供给模式的探讨［J］.电网技术，2009，33 (4):1 -5.

［2］Wirasingha S G，Emadi A.Classification and review of control strategies for plug-in hybrid electric vehicles［J］.IEEE Trans on Vehicular Technology，2011，60(1):111 -122.

［3］赵俊华，文福拴，杨爱民，等.电动汽车对电力系统的影响及其调度与控制问题［J］.电力系统自动化，2011，35 (14):2 -10.

［4］Clement-Nyns K，Haesen E，Driesen J.The impact of charging plug-in hybrid electric vehicles on a residential distribution grid ［J］.IEEE Trans on Power Systems，2010，25 (1):371 -380.

［5］Vlachoglannis J G.Probabilistic constrained load flow considering integration of wind power generation and electric vehicles ［J］.IEEE Trans on Power Systems，2009，24 (4):1808 -1817.

［6］Capion K.Optimized charging of electric drive vehicles in a market environment ［D］.Technical University of Denmark:RisΦ National Laboratory for Sustainable Energy，2009.

［7］陆凌蓉，文福拴，薛禹胜，等.计及可入网电动汽车的电力系统机组最优组合［J］.电力系统自动化，2011，35 (21):16 -20.

［8］赵俊华，文福拴，薛禹胜，等.计及电动汽车和风电出力不确定性的随机经济调度［J］.电力系统自动化，2010，34 (20):22 -29.

［9］蔡秋娜，文福拴，薛禹胜，等.基于SCUC 的可入网混合电动汽车优化调度方法［J］.电力系统自动化，2012，36 (1):38 -46.

［10］王蓓蓓，李 扬，高赐威.智能电网框架下的需求侧管理展望与思考［J］.电力系统自动化，2009，33(20):17 -22.

［11］Sortomme E，El-Sharkawi M A.Optimal charging strategies for unidirectional vehicle-to-grid ［J］.IEEE Trans on Smart Grid，2011，2 (1):131 -138.

［12］Peterson S B，APT J，Whita Tacre J F.Lithium-ion battery cell degradation resulting from realistic vehicle and vehicle-to-grid utilization ［J］.Journal of Power Sources，2010，195 (8):2385 -2392.

［13］Wu Qiuwei，Nielsen A H，ØSTERGAARD J，et al.Driving pattern analysis for electric vehicle (EV)grid integration study ［C］.Chalmers Lindholmen Gothenburg，Sweden:Proceedings of 2010 IEEE PES Innovative Smart Grid Technologies Conference in Europe (ISGT Europe)，2010.1 -6.

［14］Carrion M，Arroyo J M.A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem ［J］.IEEE Trans on Power Systems，2006，21 (3):1371 -1378.

［15］Kazarlis S A，Bakirtzis A G，Petridis V.A genetic algorithm solution to the unit commitment problem ［J］.IEEE Trans on Power Systems，1996，11 (1):83-92.