一种基于机电波理论的电网扰动在线定位方法

燕跃豪，毕天姝，杨奇逊

(华北电力大学 新能源电力系统国家重点实验室，北京102206)

0 引 言

获得可以为故障处理争取宝贵时间，对电网安全稳定运行至关重要。总体来说，电网常见扰动可以分为短路和切机/切负荷这两类。其中短路是典型的电磁暂态过程，电压、电流变化剧烈，持续时间较长，暂态能量较大。而对于切机/切负荷扰动来说，由于单个发电机/负荷容量与整个电网相比较小，使得切机/切负荷对电网电压影响也很小，电磁暂态过程持续时间较短且能量较小，可以视为机电暂态过程。

目前关于大电网扰动定位主要基于故障行波的方法［4，5］。行波定位的关键是时间的同步及行波波头的捕捉，其准确度主要受GPS 时钟的稳定

随着互联大电网规模的增加，电网扰动的影响范围也越来越大，因局部扰动引发大规模电网事故的危害性也日益增加［1～3］。扰动信息的及时性及精度、电压过零附近时刻故障、行波传输色散导致行波波头衰减及畸变等因素影响［6］。对于短路扰动，行波波头变化剧烈、暂态能量大、易于检测，因而行波定位有较好的效果。但对于没有明显电磁暂态过程的切机/切负荷扰动来说，行波波头变化平缓，行波法结果并不理想。

随着电网互联规模的逐渐增大，电网扰动引起的发电机转子角增量或频率以近似机械波的形式在电网中传播的现象日益明显［7～9］。Thorp 教授将该现象命名为机电波［10］(Electromechanical Wave)，这是研究电网机电暂态过程的一种新方法［11，12］。机电波由扰动点传播到各发电机的时间与扰动位置强相关，因此利用机电波到达各发电机的时间可以有效提取扰动位置信息。然而，受现有电网“连续体”机电波模型的限制，目前尚无利用机电波理论进行扰动定位的研究见诸报道。

本文提出了一种以WAMS 系统为平台、以机电波到达时间为信息、基于最小距离分类器的电网扰动定位方法。根据扰动后发电机频率在稳态时的短期波动特性以及机电波到达后的单调特性，提出了基于滑动数据窗的机电波到达时间在线辨识方法，能够在线快速获得待检时间向量。通过电网的框架结构模型对应的无向赋权图，借助全局最短路径搜索的Floyd 算法，构建了机电波在整个电网中传播时间组成的参考时间矩阵。通过最小距离分类器求得扰动位置。仿真结果表明，算法能有效识别扰动位置。

1 基于滑动数据窗的机电波到达时间在线辨识方法

构建待检时间向量需要获取准确的机电波到达时刻。通过区分系统正常运行状态及机电波到达后PMU 实测频率的变化特征，可以有效判断出机电波到达各发电机的时刻。

1.1 PMU 实测发电机频率特性分析及特征函数构建

在电网正常运行工况下，发电机频率保持相对稳定的状态，仅因负荷随机波动引起频率以较短的周期在50 Hz 附近波动(见图1)。

当机电波到达后，由于受持续不平衡功率的影响，发电机将产生加速或减速，从而使频率在一定时间内呈现单调上升或下降趋势(见图2)。

图1 稳态运行时的PMU 实测发电机频率Fig.1 Frequency of generator measured by PMU during steady state of power system

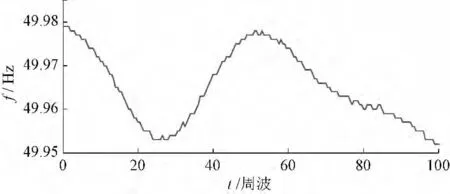
图2 机电波到达后的PMU 实测发电机频率Fig.2 Frequency of generator measured by PMU after the arrival of electromechanical waves

通过对比图1 和图2 可以发现，稳态时发电机频率的短周期波动性与机电波到达后的长期单调性的区别非常显著。在此，引入时间序列CF(i)(称之为特征函数)并定义为

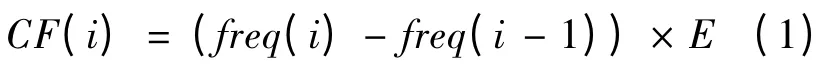
式中:freq(i)表示第i 时刻发电机的PMU 实测频率;K 表示放大倍数(freq(i)－freq(i－1)的数量级为1e－3，为便于计算，K 一般取1 000)。

图1 所表示的稳态运行时发电机频率对应的特征函数CF 见图3。从图中可以看出，此时CF为正或负的情况间隔出现。可以推断稳态特征函数CF 在一定时段内的代数和较小，甚至接近于零。

图4 为图2 表示的机电波到达后发电机频率对应的特征函数CF。从图中可以看出，此时CF将出现长时间持续为正或负的情况。可以推断从机电波到达时刻开始，CF 在一定时段内的代数和将会单调增加或减小。

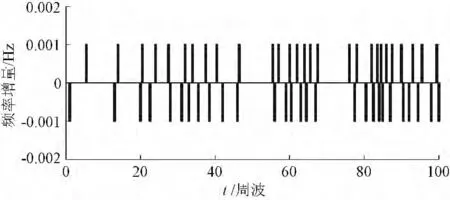
图3 稳态运行时发电机频率相对增量Fig.3 Relative increment of generator frequency during steady state of power system

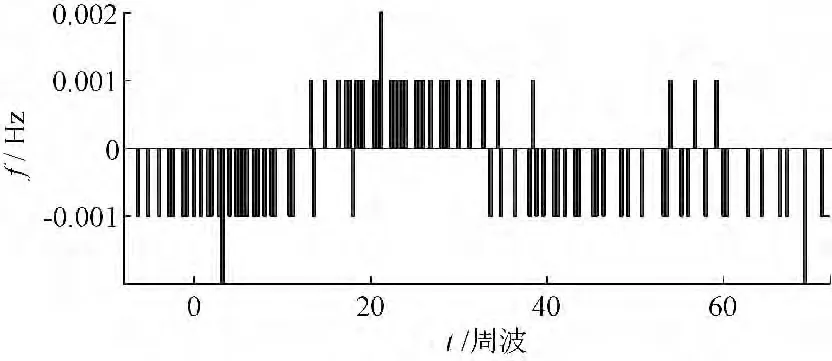
图4 机电波到达后发电机频率相对增量Fig.4 Relative increment of generator frequency after the arrival of electromechanical waves

1.2 滑动数据窗法

由以上分析可知，特征函数CF 能有效区分系统稳态时以及机电波到达后发电机频率的特征。根据发电机频率特征函数的变化规律，本文提出基于频率特征函数滑动数据窗的机电波到达时间辨识方法。首先，对于第k 点实测频率，取该点前(左侧)M 点数据构成数据窗W1，后(右侧)N 点数据构成数据窗W2。分别定义W1和W2上的函数L1和L2为

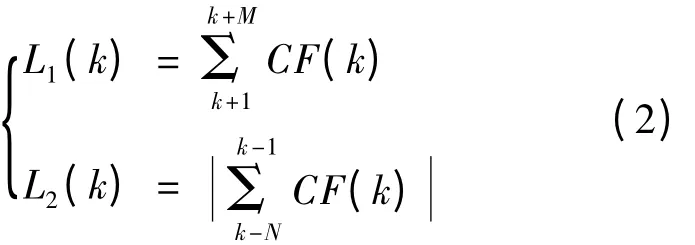
定义第k 点的判别函数R(k)为

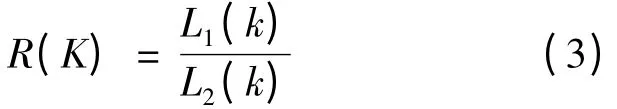
系统稳态运行时，由于特征函数CF 的短周期波动性，因正负抵消使得各时刻L1为数值较小，L2同样为数值较小的正数。可知在稳态时，|R|在零值附近振荡。当第k 时刻发生扰动时，随着第k 点右侧数据首先进入数据窗W1，引起L1的单调增大或减小。但此时第k 点右侧数据还未进入数据窗W2，L2仍处稳态阶段，其值仍为较小的正数，从而引起R 的值单调增大或减小。

随着第k 点右侧数据首先进入数据窗W2，L2的值将迅速增大，而此时受数据窗长度的限制，L1的值不变或者开始产生反向变化，使得R 的值也反向变化。即只有在第k 点处于数据窗W1和W2交界处时，R 的值才能取得极大值。

数据窗长度M 和N 的选择要以增助机电波到达特征以及减少误判为目的。考虑发电机频率单调变化的时间范围，M 取40 比较合适(根据PMU 每周波上送2 个的频率数据的设置，机电波到达时刻的判别会滞后实时数据20 个周波)。为抑制机电波到达后引起的频率长期摆动，N 适宜取30。基于以上分析，本文提出基于滑动数据窗的机电波到达时刻判断规则:

(1)R 为局部极大值;

(2)|R|≥25。

图5 显示了某发电机实测频率及其对应的判别函数R 的变化规律。从图中可见，在机电波到达时刻，R 取得局部极大值，在机电波到达后的一段时间内，R 的值将呈振荡衰减的趋势，直至下一次机电波抵达。

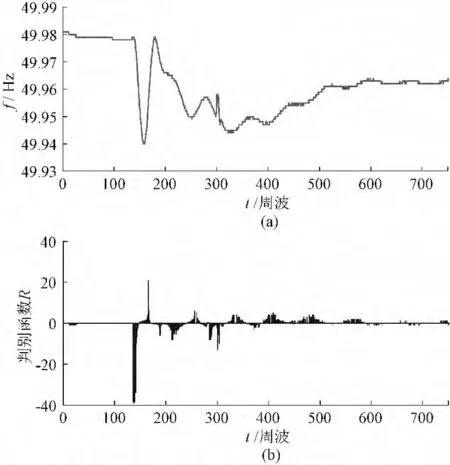
图5 PMU 实测发电机频率及其对应的判别函数RFig.5 Frequency of generator measured by PMU and the correspondingdiscrimination function R

2 参考时间矩阵快速构建方法

参考时间矩阵可以在已知电网结构及参数的情况下离线获得。然而，如果采用求解扰动后系统动态方程并对计算结果进行处理的方法将会耗费大量的时间，难以满足在线应用的要求。

2.1 电网框架结构模型概述

电网空间框架结构模型是一种研究机电波传播问题的电网等效模型［13，14］。在保证机电波传播过程等效前提下，根据转动惯量守恒及质心不变原则，将集中于节点上的发电机转动惯量在各自转动惯量作用域中按照逐级对称的方式分布到各条输电线路中，使得各线路上既包含转动惯量又包括线路电抗。以图6(a)所示的IEEE14 节点系统为例(粗体母线表示发电机母线，细体母线表示负荷母线)，虚线为发电机G3的转动惯量作用域。图6(b)为该系统对应的框架结构模型。

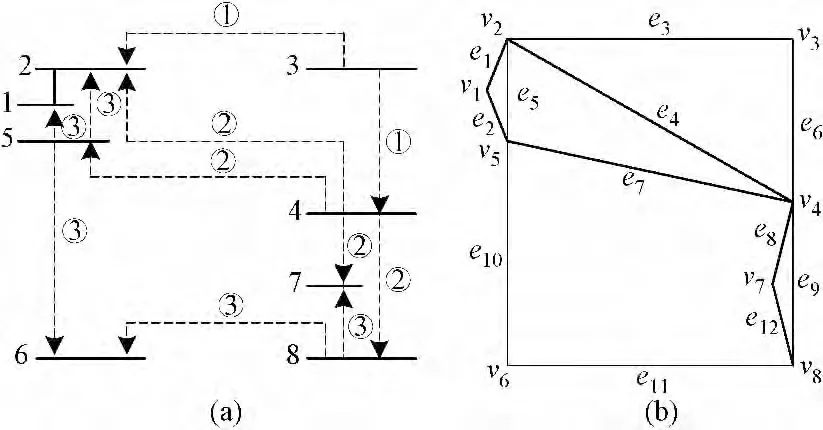
图6 IEEE-14 节点系统及其框架结构模型Fig.6 IEEE-14buspower system and its structural frame model

框架结构模型中各线路上的机电波方程为

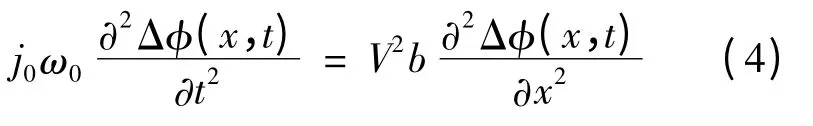
式中:j0表示是分布到该线路上的单位长度转动惯量;ω0为发电机的额定角速度;V 为线路额定电压;b 表示线路的单位长度电纳。由式(4)可得线路中机电波传播速度c 为

电网的框架结构可以用一个由n 个顶点和b条边构成的赋权图G=G(V，E，W)来表示，其中V表示图的顶点集合;E 表示图的边集合，分别对应于电网中节点和支路的集合;W 为各边的权值。如图6(b)所示，IEEE14 节点系统框架结构模型的顶点集合V ={v1，…，v8}，边集合E ={e1，…，e12}(边用两端的顶点表示，如e1=(v1，v2)等)，权值集合W={w1，…，w12}。

图G 中对边(vi，vj)赋予数量指标，称之为“权”。在电网框架结构模型中取边的权值为机电波在该边上传播所需的时间，可由其长度及式(5)所表示的机电波传播速度确定。对任一条边(vi，vj)∈E，机电波在其上的传播速度并没方向性，即由vi传播至vj所需时间与由vj传播至vi所需时间相同。因此，电网框架结构模型对应的图G 是典型的无向赋权图，使得待检时间矩阵为对称矩阵。

2.2 基于Floyd 算法的机电波传播时间搜索

在电网框架结构模型的无向赋权图中，求机电波从任一扰动点到其他发电机的传播时间就转化为图论中的全局最短路径问题。Floyd 算法(Floyd algorithm)可以获得整个图中任意两点间的最短路径［10］。其主要思想是从代表任意两个节点vi到vj机电波传播时间的带权邻接矩阵D0开始，首先计算D1，即计算vi到vj经过一次中转的所有可能路径，经过比较后选出最短传播时间路径，代替D0中对应的路径，迭代出传播时间矩阵D1，D1中各元素表示通过一次迭代后网络中任意两点间最短传播时间，也即网络中任意两点之间直接到达或只经过一个中间点时的最短传播时间路径。在此基础上依次计算D2，D3，… ，Dk－1，Dk，其中对应的元素表示任意两点间不经过中间点或最多允许经过2k－1 个中间点时的最短传播时间路径。当Dk+1=Dk时，表明得到的带权邻接矩阵Dk反映了所有顶点对之间的最短传播时间信息，称为最短传播时间矩阵。

结合电网框架结构，采用Floyd 算法搜索机电波传播时间的流程如下:

(1)将作初始机电波传播时间矩阵D0=式中:

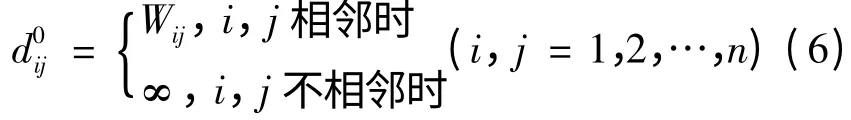
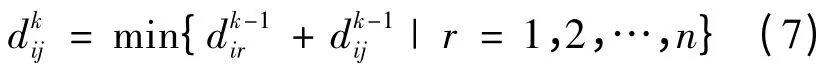
(3)若Dk+1=Dk则终止迭代;否则，返回第(2)步。

针对电网框架结构模型的无向赋权图，借助Floyd 算法，可以获得电网的最短传播时间矩阵。从中提取某扰动源达到所有发电机的最短传播时间元素组成参考时间向量，再由所有扰动源产生的参考时间向量构成参考时间矩阵。

3 基于有序最小距离分类器的电网扰动源定位方法

最小距离分类是按照模式与各类代表样本的距离进行模式分类的一种统计识别方法。在这种方法中，被识别模式与所属模式类别样本的距离最小。假定c 个类别代表模式的特征向量用R1，… ，Rc表示，x 是被识别模式的特征向量，|x-Ri|是x 与Ri(i=1，2，… ，c)之间的距离，如果|x-Ri|最小，则可把x 分为第i 类。

设电网的框架结构模型共有m 个顶点，其中包括mG个发电机节点。含在每个顶点上设定扰动，则全系统共m 个预置点。由无向赋权图可以获得机电波在各节点传播所需的时间。在此基础上，借助图论中最短路径搜索算法即可得到机电波从预置点i 传播到各发电机顶点j 所需的时间ti，j，进而mG维的参考时间向量

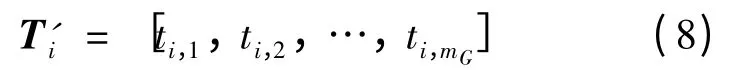
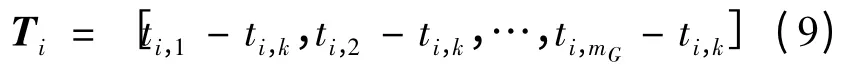
由m 个预置点的参考时间向量Ti可以构成mG×m 维的参考时间矩阵:

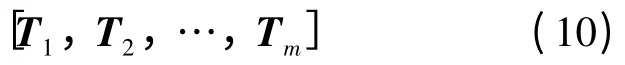
通过上文第1 节中方法可以确定机电波到达发电机的时刻构成的mG维待检时间向量T0:

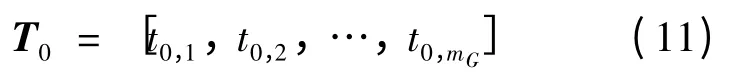
最小距离分类器采用欧式距离进行模式识别，其规则可以表示为

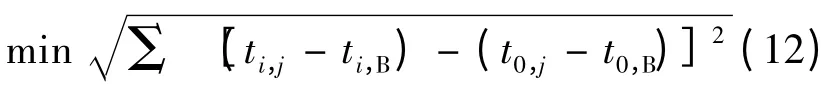
式中:i=1，2，… ，m;j=1，2，…，mG，ti，B和t0，B分别表示参考时间向量中和待检时间向量的最小值(即机电波最早到达发电机的到达时刻)。用式(12)计算待检时间向量与所有参考时间向量的欧式距离，其中与待检时间向量具有最小欧式距离的参考时间向量所对应的预置点的位置即为扰动发生位置。

然而，如果直接对全部m 个预置点采用式(12)进行判别将会耗费较长时间。由于扰动发生的位置不同，机电波到达各发电机的时刻呈现一定的先后顺序。因此可以按照机电波到达时序将参考时间向量集合分为N 个子集，每个子集具有相同的机电波到达时序。在获取待检时间向量后，就可以仅对与其具有相同时序的参考时间向量使用最小距离分类器，从而极大地缩短计算时间。基于机电波到达时间的电网扰动定位算法的整体流程见图7。

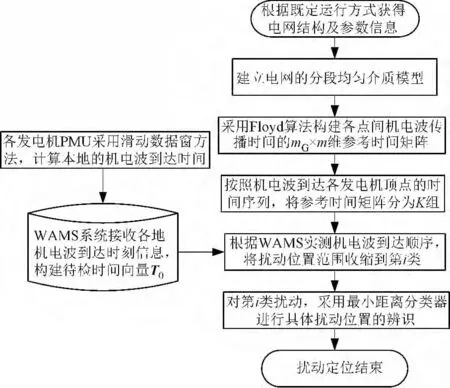
图7 算法总体流程图Fig.7 Flow chart of the proposed algorithm

4 算法验证

为验证所提算法的准确性，本文以IEEE118节点典型系统为例，在1 号发电机上施加频率为2 Hz的正弦型有功功率扰动。使用PSD-BPA 仿真软件和基于电网框架结构模型的机电波理论获得发电机频率变化曲线一致性较好，图8 选取两种方法差异最大的12 节点发电机和65 节点进行比较，说明了机电波理论的有效性。

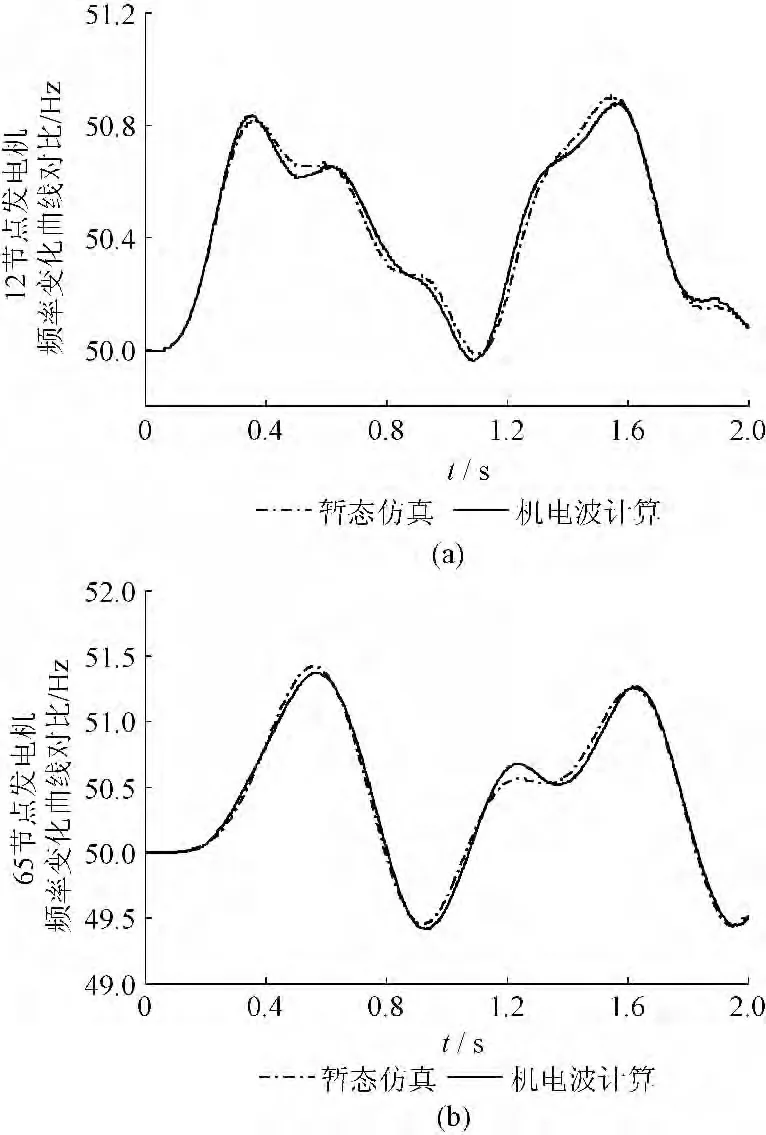
图8 发电机频率对比图Fig.8 Comparison of frequency of generators

假设通过WAMS 系统采集到的机电波到达所有发电机节点的顺序及到达时间如表1 所示，由此可以构建待检时间向量T0。

利用本文所提出的有序最小距离分类器算法，可得当节点1，2，3 发生扰动时，具有与本算例相同的扰动到达时间序列。上述3 个参考时间向量与待检时间向量的欧氏距离分别为173 ms，215 ms 和241 ms，可知由1 节点发生扰动构成的参考时间向量与待检时间向量的距离最小(两者的对比见图9)，可以确定扰动发生于1 节点上。通过以上算例说明了本文所提算法的正确性，在对其他节点进行的扰动分析也取得了准确的定位结果。

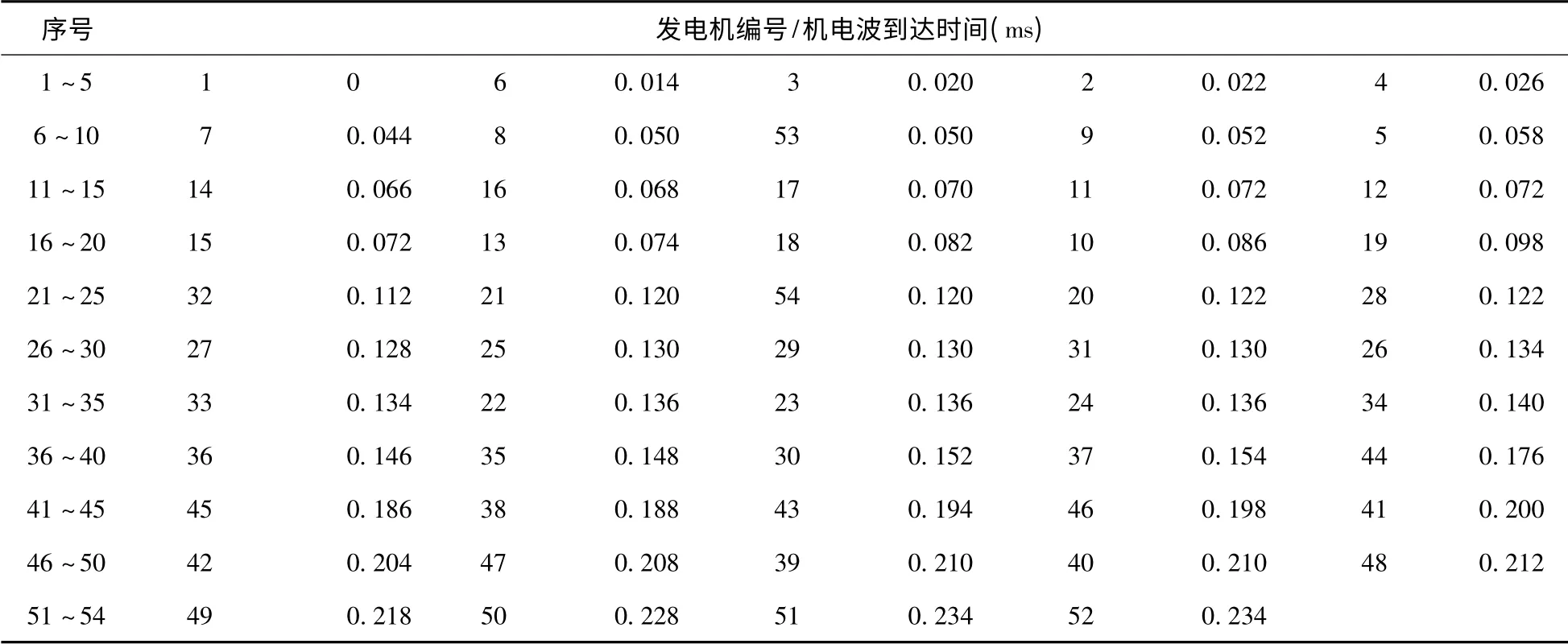
表1 IEEE-118 系统扰动后发电机的转子角增量Tab.1 Incremental rotor angles of IEEE-118bus system after disturbance

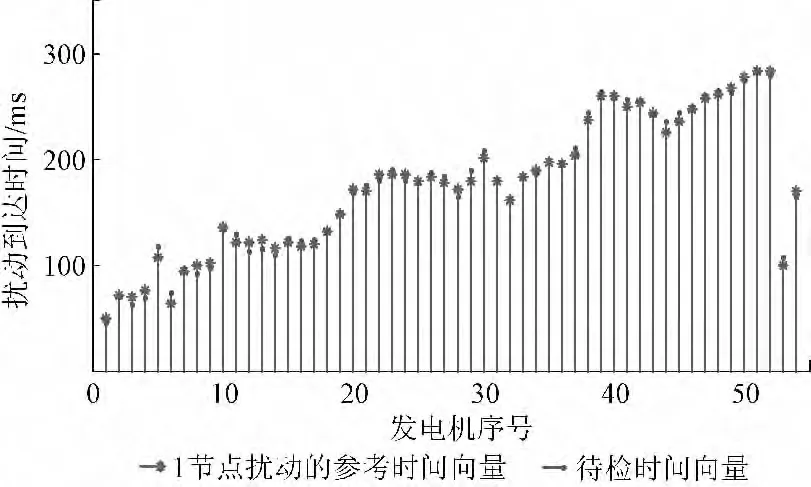
图9 搜索算法与仿真所得的机电波到达时间及偏差Fig.9 Arrival time and differences of electromechanical wave from searching algorithm and simulation

5 结 论

利用机电波理论进行扰动定位有着准确的定位效果，特别是对于行波法不能准确识别的切机/切负荷扰动，机电波方法也有良好的适应性。本文所提的扰动定位方法可以基于现有的WAMS系统主站而不需要增加新的设备，具有较好的可行性。不足之处是需要大约20 周波的时间窗。

基于本文所提出的扰动定位方法，进一步结合机电波在电网中的传播机理，可以为基于事件型的电网广域预警系统及电网主动安全控制理论的研究提供新的思路。

［1］袁季修.防御大停电的广域保护盒紧急控制［M］.北京:中国电力出版社，2007.34 －86.

［2］贺仁睦，韩志勇，周密，等.互联电力系统未知机理低频振荡分析［J］.华北电力大学学报(自然科学版)，2009，36 (1):1 －4.

［3］艾欣，崔明勇，雷之力.电力系统连锁故障研究综述［J］.华北电力大学学报(自然科学版)，2008，35 (6):44 －51.

［4］曾祥君，尹项根，陈德树，等.基于整个输电网GPS 行波故障定位系统的研究［J］.电力系统自动化，1999，(10):8 －10.

［5］曾祥君，尹项根，林福昌，等.基于行波传感器的输电线路故障定位方法研究［J］.中国电机工程学报，2002，22 (6):42 －46.

［6］严凤，杨奇逊，齐郑，等.基于行波理论的配电网故障定位方法的研究［J］.中国电机工程学报，2004，24 (9):37 －43.

［7］Semlyen A.Analysis of disturbance propagation in power systems based on a homogeneous dynamic model［J］.IEEE Transactions on Power Apparatus and Systems，1974，PAS-93 (2):676 －684.

［8］王德林，王晓茹，Thorp J S.电力系统的连续体系机电波模型［J］.中国电机工程学报，2006，26(17):30 －37.

［9］王德林，王晓茹.电力系统连续体模型中机电波传播特性研究［J］.中国电机工程学报，2007，27(16):43 －48.

［10］Thorp J S，Seyler C，Phadke A G.Electromechanical wave propagation in large electric power systems［J］.IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications，1998，45 (6):614－622.

［11］Parashar M，Thorp J S，Seyler C.Continuum modeling of electromechanical dynamics in large-scale power systems ［J］.IEEE Transactions on Circuits and Systems I:Regular Papers，2004，51 (9):1848 －1858.

［12］吴晋波，文劲宇.基于机电波传播理论的柔性功率调节器稳定控制方法实验研究［J］.电工技术学报，2012，27 (3):205 －211.

［13］Yan Yuehao，Bi Tianshu，Yang Qixun.The sectionalized homogeneous model of power systems and its analytical solution ［C］.Vancouver，BC，Canada:Power and Energy Society General Meeting (PES)，2013.1 －5.

［14］Yan Yuehao，Bi Tianshu，Yang Qixun.A new modeling approach of power networks for disturbance propagation study ［C］.Berlin，Germany:Security in Critical Infrastructures Today，2013.1 －6.