基于尺度比确定工程椭球在隧道独立控制网中的应用
2014-07-25肖雁峰
肖雁峰
(中铁第四勘察设计院集团有限公司,湖北武汉 430063)
基于尺度比确定工程椭球在隧道独立控制网中的应用
肖雁峰
(中铁第四勘察设计院集团有限公司,湖北武汉 430063)
为提高隧道独立控制网的精度,减少隧道独立控制网的投影变形,需要建立工程椭球。将求定的相对于实测边长的尺度比等价转换为抵偿投影面的高程值,从而求出工程椭球长半径,建立工程椭球,再在该工程椭球下进行一点一方向平差,减少隧道独立控制网的投影变形,提高隧道独立控制网的精度。
投影变形 工程椭球 隧道独立控制网
1 概述
隧道独立控制网精度的高低,直接影响到隧道的贯通精度,要提高隧道独立控制网的精度,则需要减少投影变形的影响。文献[1]指出只要选择合适的高程投影面进行投影,则在该参考面上的长度变形为零,文献[2]认为在一定精度范围内对较小的区域是可以的。文献[3]在常规投影变形处理方法的基础上,介绍了尺度强制约束法和投影面重新选择两种投影变形的处理方法,并通过试验证实了这两种方法只能适应较小的区域。隧道独立控制网属于较小的区域,文献[3]中介绍的两种投影变形处理方法适合于隧道独立控制网,文献[4]介绍的尺度强制约束法,当约束条件较多时,显示不出该方法的优越性,但在隧道独立控制网平差时,采用一点一方向平差,该方法平差约束条件较少,可有效减少地面网点的固有误差对GPS网型的扭曲,不会改变平差后GPS网的相对关系。因此,在独立控制网的工程椭球参数加入尺度比,可有效减少投影变形的影响。文献[5]介绍了几种建立独立坐标系的数学模型,通过几种建立独立坐标系的数学模型比较分析,椭球膨胀法更适合于建立工程椭球基础上的独立坐标系。
2 基于实测边长确定尺度比以及尺度比确定抵偿投影面高程
设两个已知点M、N坐标值为(Xm、Ym),(Xn、Yn),其实测平距为Dmn,GPS控制点反算边长为Smn,则可确定该区域尺度比K为
(1)
式(1)便是相对于实测地面控制网的边长归算尺度比。
综合抵偿投影面方法和尺度比强制约束方法的优缺点,可以将相对于实测边长的尺度比残差通过抵偿投影面方式进行处理。 边长投影变形ΔD为
(2)
实测边长归算至参考椭球面上的变形为ΔS1。
(3)
则
(4)
为了对尺度比残差进行抵偿,则抵偿面高程值Hm可表达为
(5)
Hm就是基于尺度比残差确定的抵偿投影面高程值。
3 工程椭球参数计算
参考椭球面是一个椭球曲面,其不同位置的半径不同,但椭球不同位置半径可通过椭球参数确定,根据所确定的测区抵偿面高程确定对应的工程椭球参数,采用文献[5]中介绍的椭球膨胀法进行椭球长半轴的计算,以WGS84椭球长半轴为基准,工程椭球长半轴计算如式(6)所示
(6)
(7)
(8)
式中a84、e84——WGS84椭球的长半轴和扁率;
Bm——工程测区的平均纬度;
Hm——基于尺度比残差确定的抵偿投影面高程值;
hi——i点的大地高;
Hi——i点的高程;
n——求算ζ的卫星控制点与水准同测点的个数;
N——工程测区中心的卯酉圈曲率半径;
ζ——工程测区平均高程异常。
投影面选择工程测区的平均高程面,中央子午线取隧道进、出口的平均经度。
(9)
4 施工坐标计算
独立控制网投影平面通过建立一个工程投影面,采用直接投影法进行施工坐标计算。直接投影法是以工程椭球为参考椭球,将无约束网平差WGS-84结果直接投影至工程椭球相切的高斯平面上(该平面的高程与工程平均高程相等)。
(10)
(11)
(12)
式中x0、y0——施工坐标系起算坐标;
as——施工坐标轴在施工坐标系中的方位角;
ag——施工坐标轴在高斯平面坐标系中的方位角。
5 工程实例分析
清凉山隧道位于秦岭北麓低中山区陕西省户县境内,平均海拔1 400 m,最高海拔为1 580 m。起止里程DgK56+156~DgK68+709,隧道长度12 553 m,是西成铁路客运专线中的一个长大隧道。其中埋设GPS控制点26个,联测CPⅠ、CPⅡ控制点4个。
施工坐标计算采用工程椭球直接投影法一点一方向平差计算施工坐标。以清凉山隧道出口左线中线投点(TY05-1A,直线上的中线点)为坐标起算点,其坐标假定为:X0=40 000.000,Y0=60 000.000,将X轴(TY05-1A~TY04-2)的坐标方位角设为 180°00′00″,坐标投影面为隧道线路平均高程面(H=800 m)。用WGS-84无约束平差所获得的大地坐标,按(10)、(11)式计算GPS控制点在施工坐标系中的坐标。
(1)加入尺度改正与未加入尺度改正坐标比较
从图1可以看出,从隧道起点TY05-1A,随着长度增加,坐标较差越来越大,隧道终点TY03-1加入尺度改正与未加入尺度改正的坐标较差为北方向为36.5 mm,东方向为16.4 mm,因此尺度改正对隧道独立控制网坐标影响较大。

图1 加入尺度改正与未加入尺度改正坐标较差
(2)加入尺度改正与未加入尺度改正反算坐标与测距仪实测边长比较
为了验证加入尺度改正的坐标是否更接近实测边长值,进行了一个实验,对能满足通视条件的边长都利用测距仪进行测量,并将边长投影改化。
将投影改化后的实测边长与加入尺度改正与未加入尺度改正坐标反算边长进行比较,通过43条坐标反算边长和实测经投影改化的边长进行比较,从图2可以看出,加入尺度改正的坐标反算边长和实测经投影改化的边长更吻合,未加入尺度改正的边长与实测经投影改化的边长较差与边的长度有关,较差最大为-12.9 mm。
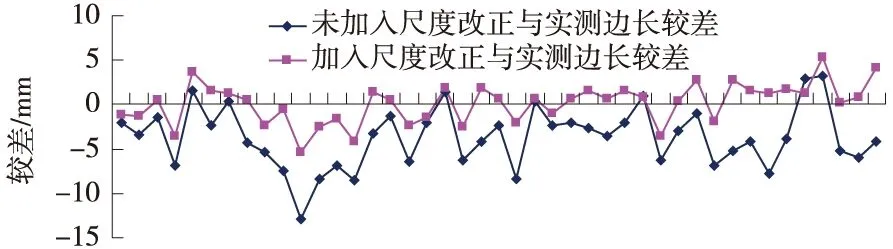
图2 加入尺度改正与未加入尺度改正坐标反算边长与测距仪实测投影改化边较差
6 结论
经理论和实践证明,在隧道独立控制网中加入尺度改正,可保证坐标成果反算边长与实测边长一致,减少隧道独立控制网的投影变形,提高隧道独立控制网的精度。
[1] 孔祥元,梅是义.控制测量学(下)[M].武汉:武汉测绘科技大学出版社,1996:89-91
[2] 刘大杰,施一民.全球定位系统(GPS)的原理与数据处理[M].上海:同济大学出版社,1997:56-58
[3] 范一中,王继刚,赵丽华.抵偿投影面的最佳选取问题[J].测绘通报,2002(2):20-22
[4] 高成发.GPS工程控制网投影变形的处理[J].测绘工程,1999(4):67-69
[5] 李祖锋.基于尺度比确定工程参考椭球长半径[J].测绘通报,2010(增刊):137-138
[6] 梁永.高速铁路测量建立独立坐标系的数学模型[J].铁道工程学报,2006(10):33-35
[7] 杨柳.高铁测量中投影变形处理方法探讨[J].北京测绘,2012(1):44-45
ApplicationofProjectEllipsoidBasedonScaleProportioninTunnelIndependentControlNetwork
XIAO Yan-feng
2014-01-10
肖雁峰(1979—),男,硕士,工程师。
1672-7479(2014)02-0047-02
P282.2
: B
