80 m简支钢箱梁剪力滞系数研究
2014-07-25刘信斌
刘信斌
(中铁上海设计院集团有限公司,上海 200070)
80 m简支钢箱梁剪力滞系数研究
刘信斌
(中铁上海设计院集团有限公司,上海 200070)
多国规范中均给出了在没有精确算法时建议的剪力滞系数。为精确分析杨梅州大桥80 m简支钢箱梁跨中截面的剪力滞效应,分别按平面梁单元与空间壳单元进行建模分析,对其在自重、二期恒载、均布线荷载、跨中集中力作用下的应力结果进行了比较,准确得到了该简支钢箱梁的剪力滞系数。
杨梅州 钢箱梁 剪力滞 有限元分析
本研究结合国内某大桥进行,大桥由西引桥、主桥和东引桥组成,主桥孔跨组合:(40+90+70+300+20) m西悬索桥+80 m简支钢箱梁+(20+240+55+75+30) m东悬索桥。钢箱梁采用简支结构时跨度达80 m,国内还没有类似工点,有必要对其结构的应力状态进行更为准确的分析,故需对本简支钢箱梁的剪力滞系数进行研究。
1 结构尺寸及计算模型
1.1 结构尺寸
简支钢箱梁采用双箱结构,之间采用横隔板连接,箱梁总宽29 m,梁高3.5 m,各部位厚度为:顶板20 mm、底板30 mm、腹板16 mm、横隔板14 mm、U肋8 mm、板肋12 mm,见图1。简支钢箱梁采用板式横隔板和框架式横隔板间隔布置,板式横隔板间距6 m,每两个板式横隔板之间有两个间距2 m的框架式横隔板。
1.2 平面梁单元模型
平面梁单元模型采用MIDAS进行计算,共划分为17个节点,16个单元,采用平面梁单元,其中横隔板重量按与空间壳单元模型支反力差均匀加载到桥面上,二期恒载及活载按纵桥向与空间壳单元模型相等进行加载(如图2所示)。
1.3 空间壳单元模型
空间计算模型采用ANSYS进行计算,共划分为265 300个节点,361 102个单元,采用shell63单元。模型的坐标系原点取在桥面端部,Z轴为横桥向,Y轴为竖向,X轴为纵桥向。箱梁横断面、横隔板及全桥整体模型如图3所示。
2 规范中剪力滞系数计算方法
通过搜集资料,找出了《钢桥规范(征求意见稿)》、日本学者小西一郎的《钢桥》、美国的《AASHTO规范》,英国的《BS5400规范》中关于钢箱梁有效宽度的计算方法。经过比较,发现各规范计算有效宽度的结果均较为接近,其中按小西一郎的《钢桥》计算时有效宽度最小,即剪力滞系数最大。
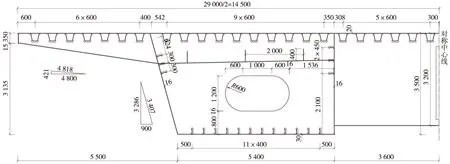
图1 半钢梁横断面(单位:mm)

图2 平面梁计算模型

图3 空间计算模型
按小西一郎的《钢桥》计算跨中截面有效宽度比
R/αt=(3 500×16)/(3 608×2×20)=0.388
AF=0.180 m2Aw=0.059 m2
1.08-0.04AF/Aw=0.958
均布荷载作用时
悬臂翼缘:Bp/L=4 582/80 000=0.057,查表得有效宽度比为0.969;
中间翼缘:B/2L=7 200/2×80 000=0.045,查表得有效宽度比为0.98;
综合系数为(9 164×0.969+19 836×0.98)/29 000=0.976;
(9 164 mm为悬臂翼缘宽度,19 836 mm为腹板中间翼缘宽度);
即相当于剪力滞系数为1/ 0.976=1.025。
集中荷载作用在跨中时
悬臂翼缘:Bp/L=4 582/80 000=0.057,查表得有效宽度比为0.761×0.958=0.729;
中间翼缘:B/2L=7 200/2×80 000=0.045,查表得有效宽度比为0.803×0.958=0.769;
综合系数为(9 164×0.729+19 836×0.769)/29 000=0.757;
即相当于剪力滞系数为1/ 0.757=1.321。
3 各种荷载作用下剪力滞系数分析
为精确分析80 m钢梁的剪力滞系数,需根据不同荷载形式进行分析,以下分别按仅作用自重、二期恒载、均布活载及集中活载进行计算,其中均布活载分为按横向车轮位置进行纵向加载和纵向仅加载到每个腹板上两种形式,集中活载分为按横向车轮位置进行集中力加载、集中加载到每个腹板及只加载到中间腹板上三种形式。
3.1 自重作用下应力分析
按平面梁单元计算时,自重作用下跨中截面顶板应力为39.2 MPa。
按空间壳单元计算时,跨中截面顶板应力矢量图如图4所示,顶板应力数值如图5。
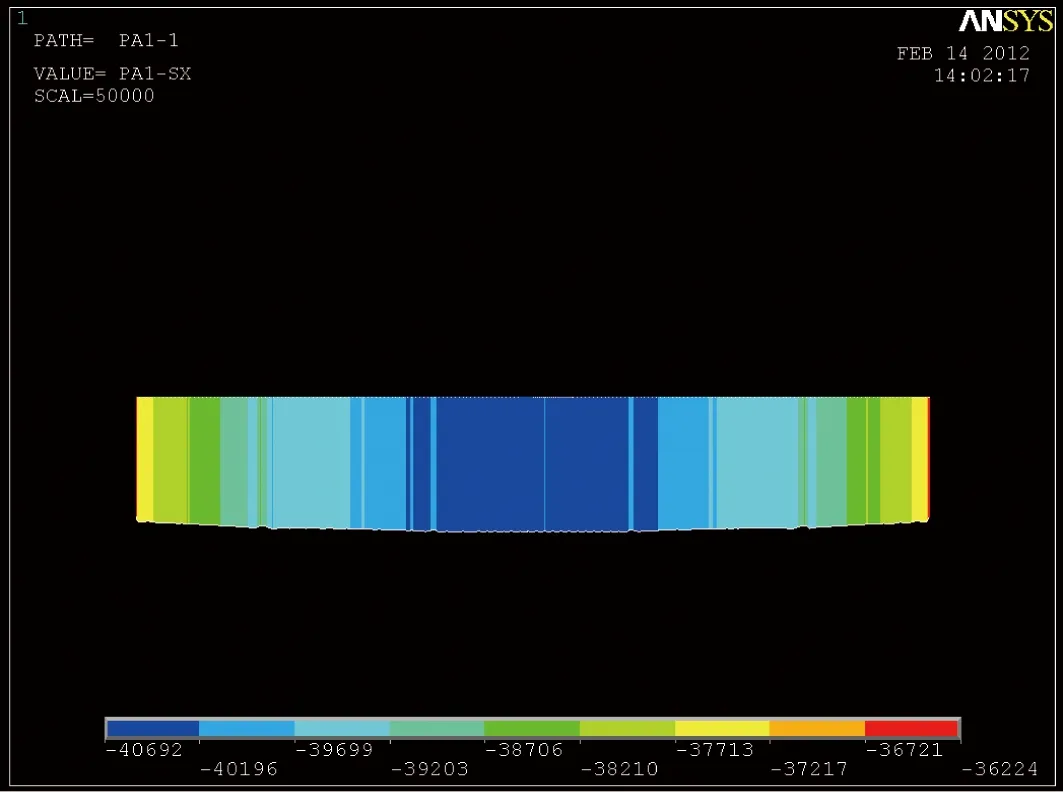
图4 跨中截面顶板应力矢量
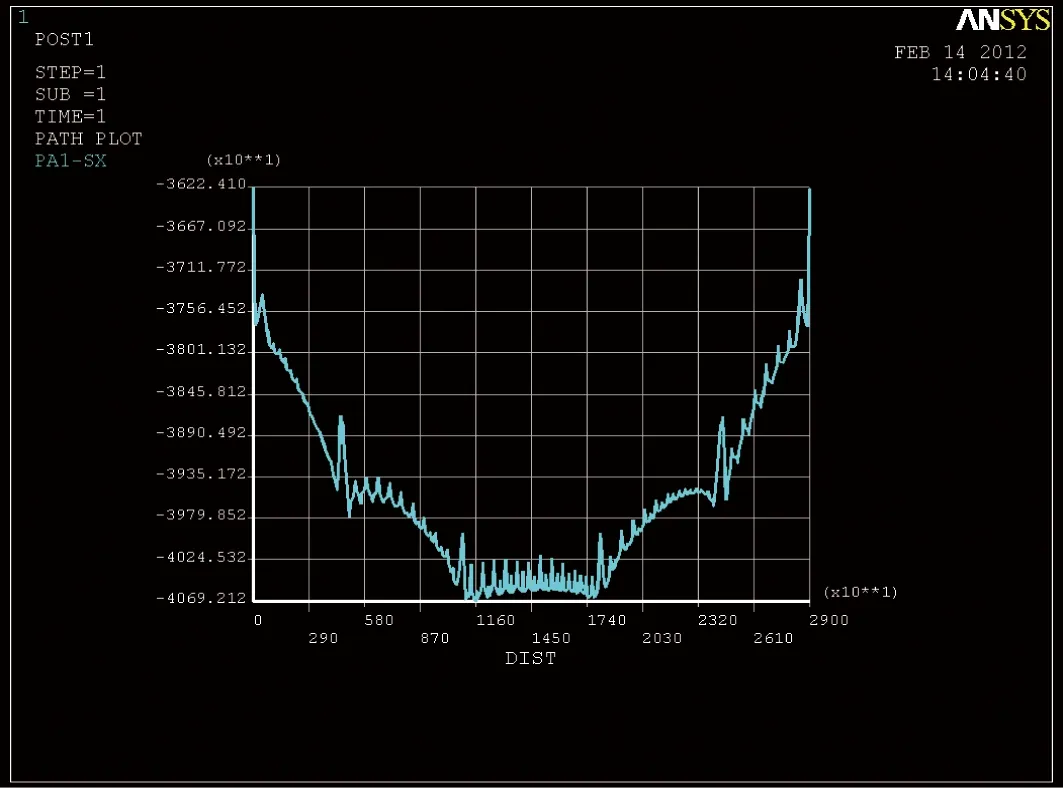
图5 跨中截面顶板应力数值
由上可知,平面梁单元模型顶板应力为39.2 MPa,空间壳单元顶板应力最大值为40.7 MPa,出现在顶板上两腹板中间部分,但此处应力包含了第二体系应力,而与腹板相交处顶板的最大应力为39.9 MPa,故在自重作用下箱梁的剪力滞系数为39.9/39.2=1.018,与规范计算值1.025较为接近。
3.2 二期恒载作用下应力分析
按平面梁单元计算时,二期恒载作用下跨中截面顶板应力为23.8 MPa。
按空间壳单元计算时,跨中截面顶板应力数值如图6。
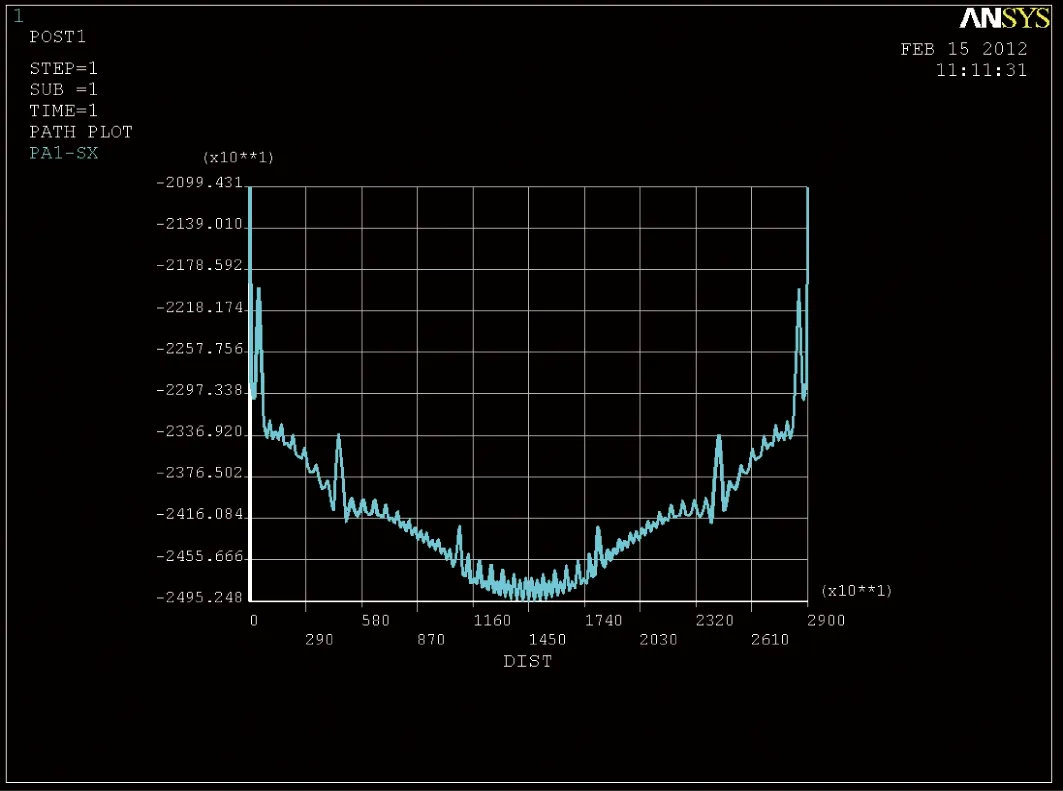
图6 跨中截面顶板应力数值
由上可知,平面梁单元模型顶板应力为23.8 MPa,空间壳单元顶板应力最大值为24.95 MPa,出现在顶板上两腹板中间部分,但此处应力包含了第二体系应力,而与腹板相交处顶板的最大应力为24.2 MPa,故在二期恒载作用下箱梁的剪力滞系数为24.2/23.8=1.016,与规范计算值1.025较为接近。
3.3 车道线荷载作用下应力分析
按平面梁单元计算时,车道线荷载作用下跨中截面顶板应力为13.4 MPa。
按空间壳单元计算时,跨中截面顶板应力数值如图7。

图7 跨中截面顶板应力数值
由上可知,平面梁单元模型顶板应力为13.4 MPa,空间壳单元顶板应力最大值为14.85 MPa,出现在荷载作用处,但此处应力包含了第二体系及第三体系应力,而与腹板相交处顶板的最大应力为13.7 MPa,故在车道线荷载作用下箱梁的剪力滞系数为13.7/13.4=1.022,与规范计算值1.025较为接近。
3.4 腹板中心线荷载作用下应力分析
按平面梁单元计算时,腹板中心线荷载作用下跨中截面顶板应力为13.4 MPa。
按空间壳单元计算时,跨中截面顶板应力数值如图8。
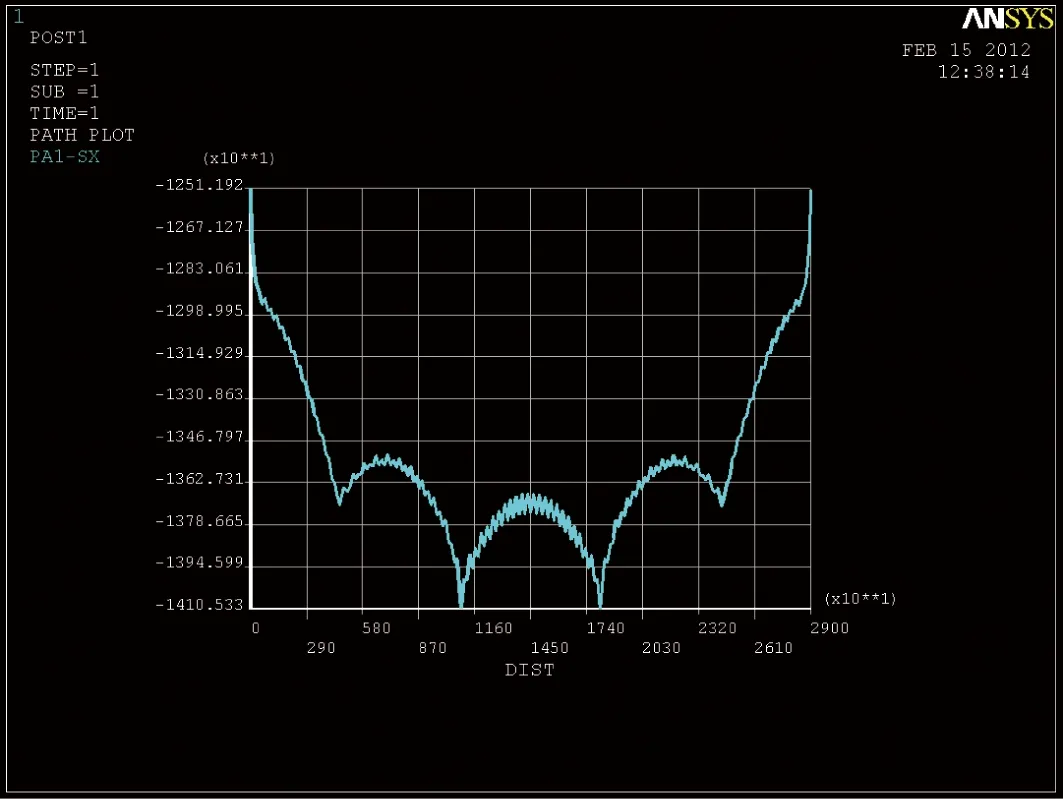
图8 跨中截面顶板应力矢量
由上可知,平面梁单元模型顶板应力为13.4 MPa,空间壳单元顶板应力最大值为14.1 MPa,出现与腹板相交处,故在腹板中心线荷载作用下箱梁的剪力滞系数为14.1/13.4=1.052,与规范计算值1.025较为接近。
3.5 车道集中力作用下应力分析
按平面梁单元计算时,车道集中力作用下跨中截面顶板应力为11.8 MPa。
按空间壳单元计算时,跨中截面顶板应力数值如图9。
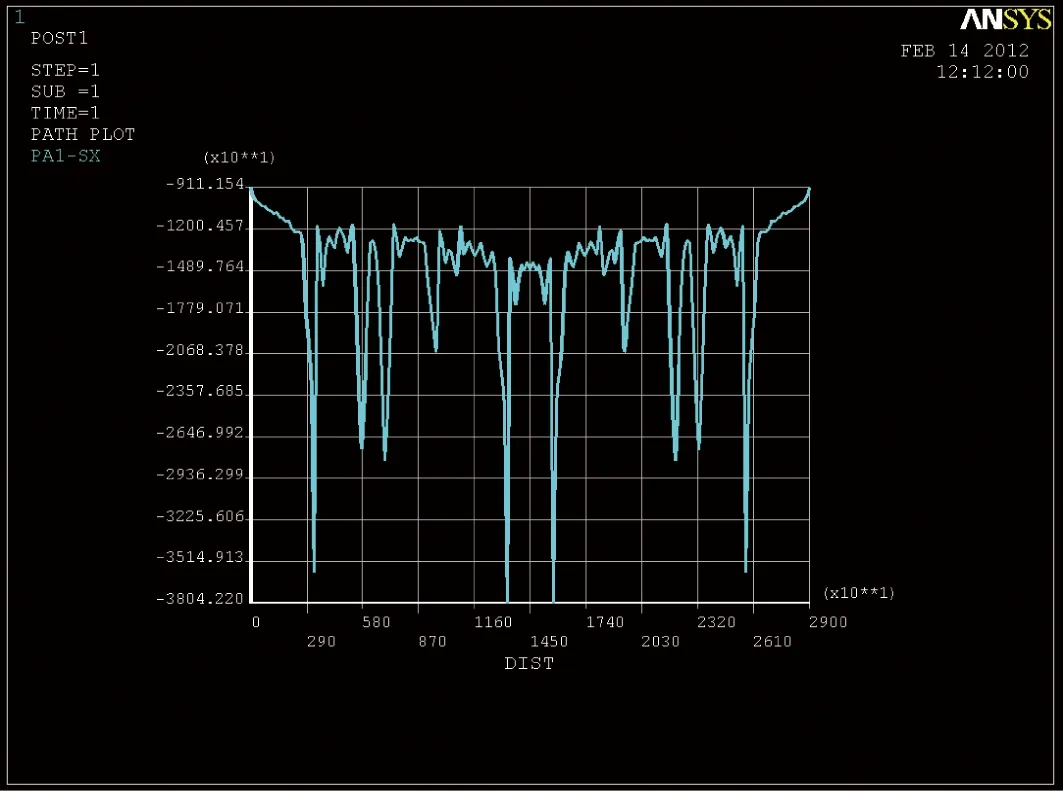
图9 跨中截面顶板应力数值
由上可知,平面梁单元模型顶板应力为11.8 MPa,空间壳单元顶板应力最大值为38.04 MPa,出现在荷载作用处,但此处应力包含了第二体系及第三体系应力,而与腹板相交处顶板的最大应力为12.0 MPa,故在车道集中力作用下箱梁的剪力滞系数为12.0/11.8=1.017,与规范计算值1.321略有区别。
3.6 腹板中心集中力作用下应力分析
按平面梁单元计算时,腹板中心集中力作用下跨中截面顶板应力为11.8 MPa。
按空间壳单元计算时,跨中截面顶板应力数值如图10。
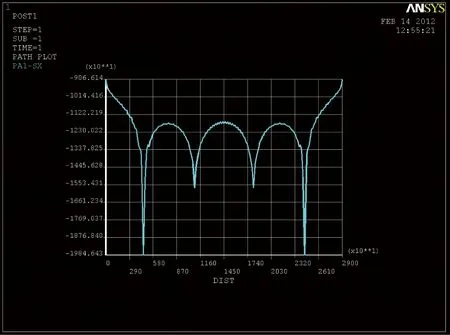
图10 跨中截面顶板应力矢量
由上可知,平面梁单元模型顶板应力为11.8 MPa,空间壳单元顶板应力最大值为19.84 MPa,出现在斜腹板与顶板相交处,而中腹板与顶板相交处的最大应力为15.53 MPa,故在腹板中心集中力作用下箱梁的剪力滞系数为15.53/11.8=1.316,与规范计算值1.321较为接近。
3.7 中腹板中心集中力作用下应力分析
按平面梁单元计算时,中腹板中心集中力作用下跨中截面顶板应力为11.8 MPa。
按空间壳单元计算时,跨中截面顶板应力数值如图11。

图11 跨中截面顶板应力矢量
由上可知,平面梁单元模型顶板应力为11.8 MPa,空间壳单元顶板应力最大值为20.2 MPa,出现在中腹板与顶板相交处,故在中腹板中心集中力作用下箱梁的剪力滞系数为20.2/11.8=1.712,与规范计算值1.321相差较多。
4 结论
根据以上分析结果汇总如表2。
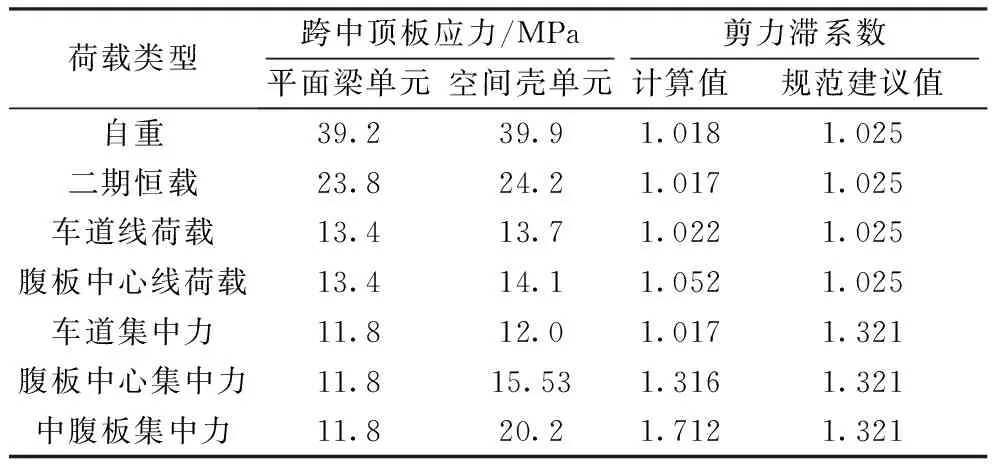
表2 跨中顶板应力计算结果汇总
由表1可以看出:
(1)在自重,二期恒载作用下,剪力滞系数计算值分别为1.018,1.017,平面梁单元计算时可按1.02采用。
(2)在车道线荷载和腹板中心线荷载作用下,剪力滞系数计算值分别为1.022,1.052,平面梁单元计算时可按1.05采用。
(3)在车道集中力、腹板中心集中力和中腹板集中力作用下,剪力滞系数计算值分别为1.017、1.316、1.712,在这3种作用方式下剪力滞系数相差较大,结合汽车活载的实际作用形式及规范建议值,平面梁单元计算时可按1.32采用。
根据本梁的应力状态,为计算时应用方便,本钢梁的综合剪力滞系数为(39.2×1.02+23.8×1.02+13.4×1.05+11.8×1.32)/(39.2+23.8+13.4+11.8)=1.064。
[1] 吴冲.现代钢桥[M].北京:人民交通出版社,2003
[2] 徐君兰,孙淑红.钢桥[M].北京:人民交通出版社,1998
[3] 郭金琼,房贞政,郑政.箱形梁设计理论[M].北京:人民交通出版社,2005
[4] 李福生.北京密云潮白河大桥钢箱梁三滑道顶推施工技术[J].铁道勘察,2013
[5] 王福兴.京杭运河常州邹区大桥钢箱梁安装施工技术[J].铁道勘察,2006
[6] 李立峰,邵旭东,易伟建,等.扁平钢箱梁局部稳定模型试验[J].中国公路学报,2007,20(3):60-65
[7] 顾兴宇,周世忠.车辆荷载下钢箱梁沥青混凝土铺装受力分析[J].东南大学学报,2001,31(6):18-20
[8] 刘世忠,欧阳永金.变截面薄壁箱梁剪力滞剪切变形效应分析[J].中国公路学报,2002,15(3):61-63
[9] 欧阳永金.大跨度比连续钢箱梁桥的剪力滞效应研究[J].世界桥梁,2009,1(4):29-32
ResearchontheShearingForceLagCoefficientof80mSimplySupportSteelBoxGirder
LIU Xin-bin
2014-02-27
刘信斌(1985—),男,2008年毕业于西南交通大学桥梁工程专业,工学硕士,工程师。
1672-7479(2014)03-0095-04
U441.+5
: A
