基于工程椭球的地方坐标系坐标换算模型比较分析
2014-07-25王国祥
王国祥
(中铁二院工程集团有限责任公司,四川成都 610031)
基于工程椭球的地方坐标系坐标换算模型比较分析
王国祥
(中铁二院工程集团有限责任公司,四川成都 610031)
精密工程测量中,为了减小投影变形,一般将国家坐标系下的成果转化到具有任意抵偿面和任意中央子午线的地方坐标系中。依据参考椭球的构造原理,在对目前常用转化计算方法分析比较的基础上,通过选取不同的参数和变换模型构造出9种不同的任意中央子午线任意投影面之间坐标计算方法,并分析每个模型的特性及适用情况,编制了CREEC GPS数据处理软件,并用工程实例数据进行分析计算与比较。
抵偿面 中央子午线 国家坐标系 地方坐标系 工程椭球
1 概述
国家高斯坐标系采用的投影面为参考椭球面,而工程控制网采用的投影面为测区某一高程面(抵偿面)。由于参考椭球面和工程控制网投影面不重合,高斯投影中产生长度变形,导致以国家高斯坐标系中的坐标反算出来的距离与工程控制网对应长度不相等。为了消除长度变形对工程产生的影响,使高程归化改正[1]和高斯投影变形之代数和尽可能小。在工程测量单位的实际应用当中,既要求选取特定的中央子午线,用国家坐标系已知点约束工程控制网,又要求投影面选用某一高程面。因此,计算时首先将国家椭球转化为具有任意抵偿面的工程椭球,即构建工程椭球;其次是选取特定的中央子午线(测区的平均经度值)将国家坐标系成果转化到地方坐标系中,供现场施工使用,即坐标投影换带计算。针对这一问题,国内外许多学者都做了比较深入的研究,但由于大家所选用的基准、参数、模型都不一样,从而使得换算出来的坐标也不尽相同。首先讨论我国常用的3种构造工程椭球和3种加抵偿高的坐标换算(共9种)方法,其次提出每个计算模型的特性及适用情况,最后采用CREEC GPS数据处理软件进行计算验证。
2 构造工程椭球
构造工程椭球的两个原则:①工程椭球的中心与国家参考椭球的中心重合,没有平移量,且使椭球的扁率保持不变。②国家椭球与地方椭球定向一致,没有旋转。构造工程椭球就是将国家椭球的长半径增大Δa,使半径增大后的工程椭球面与实际地面大致吻合,使得a1=a+Δa。各参数的关系如图1、图2所示。

图1 地形面、国家椭球面、大地水准面和工程椭球面

图2 大地高和正常高
其中:Bm——测区的平均纬度;
a——国家参考椭球的长半轴;
a1——工程椭球的长半轴;
ζ——测区平均高程异常;
Hr——投影面的正常高(平均高程面或抵偿高程面);
Hm——投影面大地高。
其中:Hm=Hr+ζ
长半轴改变量Δa的确定如下。
(1)高程直接补偿法
将投影面的平均大地高直接加到国家椭球长半轴a,即Δa=Hm,a1=a+Hm。这种构造方式适合测区的地形比较平坦时使用。
(2)法线方向增长法
假定长半轴是沿测区地面点的法线方向增加,则根据卯酉圈曲率半径N等于法线介于椭球面和短轴之间的长度,可通过测区的N确定;N与参考椭球长半轴a的关系如下
(1)
由(1)式得
(2)
(3)平均曲率半径法
通过测区的平均曲率半径确定Δa,国家参考椭球面一点的平均曲率半径与参考椭球面长半轴a关系如下
(3)
设测区的平均曲率半径为R测=Rm+Hm。由式(3)知,新椭球的长半轴的长度为
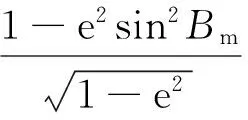

(4)
因此
(5)
根据构造出的工程椭球参数值和选用的中央子午线重新计算高斯平面坐标点的值,不同的Δa换算的结果也不相同。下面讨论3种常用的加抵偿高坐标换算方法:空间直角坐标过渡法、纬度增量法和长半轴补偿法。
3 工程椭球下的坐标换算
3.1 空间直角坐标过渡法
由工程椭球的性质可知,不同工程椭球下的空间直角坐标系是完全重合的;对于地面同一点,其在不同工程椭球下算出的空间直角坐标完全相同。其计算过程如下:
(1)以国家参考E为基准,由国家坐标系坐标(x,y),通过高斯坐标反算公式计算出经纬度(B,L)。
(2)以国家参考椭球E为基准,由大地坐标(B,L,H)按式(6)转化为空间直角坐标(X,Y,Z)。有
(6)
(3)以工程椭球E1的参数为基准,取a1=a+Δa,由空间直角坐标(X,Y,Z)按式(7)计算出大地坐标(B1,L1,H1),计算B1要用迭代方法。
(7)
(4)以工程椭球E1的参数为基准,取a1=a+Δa,由经纬度(B1,L1),通过高斯投影坐标公式计算出平面直角坐标(x1,y1),即地方坐标系坐标。
以上实现了由国家坐标系坐标通过空间直角坐标实现了到地方坐标系的换算;由地方坐标系到国家坐标系的换算只要逆向运算就可。
在步骤(2)中,计算空间直角坐标(X,Y,Z)时,必须知道测点的大地高。但在实际计算过程中,可假定换算点的大地高为零(见表1)。选取3个具有代表性的点,再将这些点从国家坐标系换算到大地坐标系中,逐一变化大地高,得到不同的结果(见表2)。
与大地高H=0 m时求得的坐标结果相比,Y坐标没有发生变化,而X坐标差值最大的点在点1中,H=5 000 m时相差1.3 mm,H=10 000时也仅相差2.5 mm。由此可知,采用空间直角坐标过渡法,将国家坐标系中坐标换算到地方坐标系坐标时,将换算点的大地高假设为零,当精度满足要求时是可行的,也可用点位高程代替大地高。

表1 3个不同的具有代表性的点

表2 坐标随大地高变化比较表 m
3.2 纬度增量法
地面点在椭球面上的位置,是由一定的元素和定位椭球所规定的,如果选择的椭球元素和定位发生变化,地面点在椭球面上的大地坐标必将随之变化。根据椭球元素和定位变化推求点的大地经纬度和大地高变化的公式,叫大地坐标微分公式
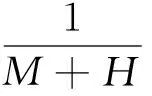

(8)

(9)
式中,da、df表示椭球元素(长半径、扁率)的变化;
dX,dY,dZ表示椭球中心变化,即椭球定位的变化。
由于工程椭球中心与国家参考椭球中心重合,椭球的扁率保持不变,由大地坐标微分公式知:测区同一点其经度不会发生变化,仅纬度将随之发生改变,随长半径而变化的纬度改变量
ΔB=Δa(Ne2sinBcosB)/(aM)=

(10)
纬度增量法的计算过程如下:
①以国家参考椭球E为基准,将点坐标(x,y)通过高斯投影反算公式计算出坐标经纬度(B,L)。
②计算出各点在新椭球E1上的纬度B1=B+ΔB。
③用(B1,L)和a1,用高斯投影坐标正算公式计算出高斯平面直角坐标(x1,y1),即地方坐标系坐标。
3.3 长半轴补偿法
对于地面同一点,假设换算前后经纬度保持不变,因此在计算时只改变长半轴a而保持投影后的经纬度值不变,通过高斯投影计算出地方坐标系中的坐标(x1,y1)。
4 算例分析
根据任意中央子午线和任意投影面的国家参考椭球长半轴的3种增大方法和坐标换算3种方法,编制了CREEC GPS数据处理软件包,并对某实例数据进行分析计算,见表3。
为了检查程序计算的精度,进行逆运算,即将地方坐标系的坐标转化到国家坐标系中,并与国家坐标系中的已知点值进行比较,见表4。
由表3、表4可以得出:
①对于同一种换算方法,在对长半轴增量Δa的取值模型不同的情况下,计算的结果也不相同。由换算前和换算后的坐标较差结果可以看出,取值模型的不同对X坐标的变化影响较大,而对Y坐标的变化影响较小。如对空间直角坐标过渡法,ΔX相互间的差值较大,最大为424.9 mm;而ΔY相互间的差值较小,最大为20.8 mm。
②对于不同的换算方法,在对长半轴增量Δa取值模型相同的情况下,空间直角坐标过渡法和纬度增量法计算出来的结果相同,而与长半轴补偿法计算出来的结果不相同。由换算方法的模型可知,对于地面同一点,在前两种方法中,该点相对于不同的工程椭球,其纬度是发生变化的;而在长半轴补偿法中,点纬度是假设固定不变的。该假设本身不严格,不符合工程椭球构造的原理,故该方法不宜采用。
③在所有的计算方法中,Δa选取的计算模型不同,其计算的结果也不相同,X坐标之间的较差大,而对Y坐标影响小。在不同的计算方法中选取不同的取值模型,产生的X较差为1.340 m,Y较差为0.034 m。

表3 基于工程椭球的地方坐标换算成果 m

表4 正算与逆算比较
④在工程椭球的构造方法中,法线方向增长法与平均曲率半径法都与测区的平均纬度Bm有关,随着Bm的取值不同,获得结果也不相同。因此,在实际使用时,应注意Bm的取值。
⑤根据程序正算和逆运算的差值可以看出,该程序计算出的坐标值精度可以达到0.05 mm,完全满足工程施工需要。
5 结论
利用工程椭球的设想,通过不同的模型构造出了9种不同的计算方法,基本上涵盖了目前各种工程中所采用的换带换投影面方法,通用性强。在由国家坐标系中的坐标向地方坐标系相互转换过程中,所选取的模型方法不同,导致求得的转化坐标也不相同。为此,提出如下建议:
(1)实际工作中,一个测区由不同的施工单位施测时,容易产生由于坐标不一致而导致施测边处出现交叉不吻合的情况;应采用相同的坐标换算模型,统一处理方案,避免产生标段间衔接不平顺问题。
(2)在由国家坐标系坐标到地方坐标系的相互转换过程中,所选取的工程椭球不同、计算模型方法不同,求得的转换坐标结果也不相同。选取不同的工程椭球和不同计算模型方法主要造成X坐标方向的差异,对东西走向的线路产生大的横向偏差,对南北走向的线路产生大的纵向偏差,所以东西走向的线路更需要注意工程椭球的构建和计算模型选取方法。
(3)测区高程异常值往往不能准确确定,当实施转换时,必须注明它的取值。高程异常值一般情况下不能忽略,若确实无法获得而忽略不计时,要特别给予说明。
(4)构造工程椭球的平均曲率半径法,工程椭球下坐标换算的纬度增量法,建议优先采用。
[1] 孔祥元,梅是义.控制测量学[M].武汉:武汉大学出版社,1996:1-116
[2] 孔祥元,郭际明,刘宗泉.大地测量学[M].武汉:武汉大学出版社,2005:1-204
[3] 刘大杰,施一民,等.大地坐标转化与GPS控制网平差计算及软件系统[M].上海:同济大学出版社,1997
[4] 董克勤.任意似椭球高斯投影的实现[J].工程勘察,1995(2)
[5] 王继刚,王坚.具有抵偿面的任意带高斯投影直角坐标系的选取方法[J],测绘通报,2002(11)
[6] 范一中,王继刚,赵丽华.抵偿投影面的最佳选取问题[J].测绘通报,2000(2)
[7] 范一中,赵丽华.任意带高斯正形投影直角坐标系的最佳选取问题[J].测绘通报,2000(8)
[8] 鲍建宽.高斯平面坐标换算到测区平均高程面上的方法[J].测绘通报,1997,9(3)
ComparativeAnalysisonCoordinationConversionModelBasedonLocalCoordinateSystemofEngineeringEllipsoid
WANG Guo-xiang
2014-02-27
中铁二院工程精调有限责任公司科研项目07185103(07-07)。
王国祥(1973—),男,1996年毕业于西南交通大学摄影测量与遥感专业,高级工程师。
1672-7479(2014)03-0001-04
P282.2
: A
