沥青路面结构厚度与模量对路表弯沉的影响分析

□文 /王晓华

JTGD50—2006《公路沥青路面设计规范》是以设计弯沉值为路面整体刚度的控制指标，对沥青混凝土面层和半刚性材料的基层、底基层拉应力是否满足容许拉应力的要求进行验算。从力学角度考虑，路面损坏状态主要是路表的过大变形、路面结构层被拉裂以及路面结构层的剪切破坏，因此应进行路面结构的力学响应分析，即对沥青混凝土面层中面层、基层和底基层各自厚度与模量对路表弯沉的影响并根据路面各结构层的主要技术要求，调整结构组成，以使设计者遵循各结构层的力学特点进行路面结构的设计。

1 有限元模型的选取

路面结构可以看成三维的工程结构物，承受任意形式的载荷，因此建立有限元模型可以实现在三维空间范围内对路面结构进行离散化并采用三维的分析方法对路面结构受力进行相应的计算。本次对路面结构力学分析中，采用多层弹性连续体系理论，把路面结构假定为弹性层状体系。

1.1 基本假定

1）各层都是由均质、各向同性的弹性材料组成，这种材料的力学性能服从虎克定律。

2）假定土基在水平方向和向下的深度方向均为无限，其上的各层厚度均为有限，但水平方向仍为无限。

3）上层表面作用有轴对称圆形均布载荷（可以是垂直均布载荷，也可以是一般圆形载荷），同时在下层无限深度处及水平无限远处应力和应变都是0。

4）层间接触面满足一定的条件，可以假定是完全连续、完全光滑，也可以介于两者之间。

5）不计路面结构的自重影响。

1.2 基本参数

为分析不同路面结构参数的改变对行车载荷作用下应力场的影响，选取一典型路面结构进行分析，各结构层及计算参数见表1。

表1 路面结构参数

式中：P为作用在车轮上的载荷，kN；p为轮胎接触压力，kPa；δ为接触面当量圆半径，m。

轮胎接地面积与轮胎压力之间的关系可以由式（2）确定。

式中：A为轮胎接地面积，cm2；P为轮胎压力，N。

随着载荷的增加轮胎的接地面积会产生变化，运用式（1）和式（2）计算出相对应的轴重、轮压与轮胎接地面积，具体计算参数见表2。

作用载荷形式为圆形均布并采用轮胎内压力作为轮胎接触压力。当量圆的半径δ可以按式（1）确定。

表2 轴重与轮压、轮胎接地面积

1.3 有限元模型

采用 ANSYS通用有限元软件进行计算，各层采用sol id 45八节点实体单元。在进行道路结构力学分析时，一般假定路面各层为平面无限大的弹性层，路基为弹性半空间体。采用有限元计算时，无法将模型的尺寸取为无穷大，因此取沥青混凝土路面长10 m，宽10 m，路基深度为10 m，水平路面为xy面，y为行车方向。网格划分尺寸为2 cm，为便于模拟实际轮胎与路面接触情况，在加载面上进行局部细化，见图1。

边界条件假设为底面没有z方向位移；左右两面没有x方向位移，前后两侧没有y方向位移，层间完全连续。考虑到路面结构的对称性，建立1/2模型，在xz面设置对称约束。

图1 有限元模型

2 面层厚度与模量的敏感性分析

2.1 沥青路面路表弯沉分析

路表弯沉是在一定载荷作用下路表面的竖向变形，是反映路面整体承载能力高低和使用状况好坏的最直观、最简单的指标。它是由路面各结构层(包括土基)各自变形的综合结果，因此该变形在一定程度上反映了路面各结构层及土基的力学性质。

以双轮组车辆载荷作用下，在路表面轮隙中心处的弯沉作为路面整体抗变形能力的指标。因此，对位移的分析，主要就是分析路表面轮隙中心处的弯沉。下面以各结构层的模量和厚度为变量，分析其变化对路表弯沉的影响。

2.1.1 沥青路面面层厚度与模量对路表弯沉的影响

以表1中拟定的路面结构参数为基础，计算不同面层厚度及模量情况下的路表弯沉值，见图2和图3。

图2 面层厚度对路表弯沉的影响

图3 面层模量对路表弯沉的影响

2.1.2 基层厚度与模量对路表弯沉的影响

以表1中拟定的路面结构参数为基础，计算不同基层厚度及模量情况下的路表弯沉值，见图4和图5。

图4 基层厚度对路表弯沉值的影响

图5 基层模量对路表弯沉值的影响

2.1.3 底基层厚度与模量对路表弯沉的影响

在其他参数不变的情况下，计算不同底基层厚度及模量情况下的路表弯沉值，见图6和图7。

图6 不同底基层厚度时的路表弯沉值

图7 不同底基层模量时的路表弯沉值

2.1.4 土基模量对路表弯沉的影响

土基是路面结构的基础，土基模量对于路面结构的受力与变形特性具有显著的影响，在其他参数不变的情况下，计算不同土基模量情况下的路表弯沉值，见图8。

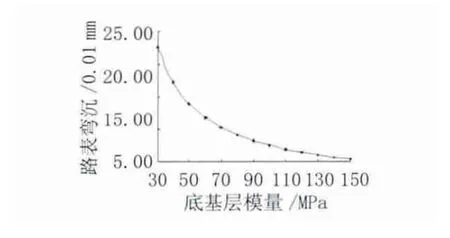
图8 不同土基模量时的路表弯沉

2.2 各影响因素与弯沉值分析

路表弯沉随着各影响因素的增大而减小，即降低路表弯沉可通过增大各结构层的模量与厚度以及土基模量来实现。弯沉值随土基模量的增大而减小幅度最大，表明土基模量对弯沉值的影响最大。而当土基模量增加到一定程度后，对降低弯沉值作用有所减缓，因此刻意继续增加土基模量对减小弯沉值意义不大。

2.3 正交试验计算结果分析

判断一个方案优劣性，不能简单利用单一指标，正交分析法是在许多可选方案中选取最优方案的有力工具，它在总体评价基础上可做出最优选择。如果综合分析各结构层的模量和厚度等11种因素对弯沉值的影响关系，分析起来比较繁琐。本文将分别论证模量和厚度对弯沉值的影响。为简化分析，将上面层、中面层、下面层假设为整体一个面层考虑，同理将上基层和下基层假设为整体一个基层考虑。分析采用的路面结构形式见表3。

表3 正交分析采用的路面结构

按模量分析，面层模量A、基层模量B、底基层模量C、土基模量D作为因子，假设4个因子之间任意两个没有交互作用。为使计算次数少些，采用3种水平的正交，见表4，路表弯沉正交计算结果见表5。

表4 因子和水平 MPa

表5 路表弯沉正交计算结果

3 结论

1）分析不同结构层模量对路表弯沉的影响，根据正交试验计算结果，各因素对弯沉的影响按从大到小顺序为土基模量＞基层模量＞底基层模量＞面层模量，这与各因素对路表弯沉的线性关系式中斜率大小反映相一致，即斜率越大，该因素对路表弯沉值的影响越明显。

2）对路表弯沉的影响按从大到小顺序为土基模量＞上基层厚度＞下基层厚度＞底基层厚度＞上基层模量＞上面层厚度＞下基层模量＞中面层厚度＞下面层厚度＞下面层模量＞底基层模量＞中面层模量＞上面层模量。

3）通过面层厚度与模量的敏感性分析，经正交试验计算得出对路表弯沉的影响按从大到小顺序，设计者可以根据各结构层的力学特点、结合当地道路用材等实际条件进行路面结构的设计。