一般尺度法的振动疲劳强化系数分析

程军圣，袁毅，喻镇涛，袁辉

(1.湖南大学汽车车身先进设计制造国家重点实验室长沙410082；2.东风汽车公司技术中心试验部，湖北十堰441004)

一般尺度法的振动疲劳强化系数分析

程军圣1，袁毅1，喻镇涛2，袁辉2

(1.湖南大学汽车车身先进设计制造国家重点实验室长沙410082；2.东风汽车公司技术中心试验部，湖北十堰441004)

在Dirlik模型的基础之上，结合一般尺度法（General scaling law）提出适用于平稳宽带随机过程的疲劳强化系数模型。一般尺度法认为结构在原始载荷和强化后载荷下的应力响应功率谱各阶谱矩成简单的线性关系；与Dirlik宽带疲劳损伤模型结合，便得到适用于平稳宽带随机过程的疲劳强化系数模型。为了验证模型的有效性，分别在原始加速度功率谱和经一般尺度法强化后的加速度功率谱载荷下；对悬臂梁采用雨流计数(Rainflow counting)和M iner损伤准则进行疲劳寿命预测，得到它们的疲劳强化系数，并与疲劳强化系数模型得到的疲劳强化系数进行对比。结果表明：提出的疲劳强化系数模型精度为99.7%，由此可验证疲劳强化系数模型的有效性。

振动与波；一般尺度法；振动疲劳；疲劳强化系数；疲劳寿命预测

疲劳失效是指零件在经历一定循环加载之后，产生裂纹并最终失效（断裂）[1]。在产品设计阶段，对产品进行耐久性分析主要采用有限元法[2，3]；在产品检验阶段，耐久性分析主要通过振动试验台试验[4]。目前很多零件的疲劳寿命都超过107次循环，称之为超高周疲劳零件[5]。对于这类零件，采用传统的疲劳试验方法是很耗时的。因此，寻求一种强化疲劳试验方法来缩短试验时间是非常必要的。

目前，国内对于振动疲劳强化试验中的关键技术—疲劳强化系数模型研究较少。国外只有Allegri研究了适用于平稳窄带随机过程的疲劳强化系数模型[6]。Allegri对平稳窄带随机过程的疲劳强化系数模型进行的推导存在两个明显问题，用随机应力响应的均方根值代替S-N曲线中的应力值，用应力响应正穿越0点的次数代替单位时间的应力循环次数。以上两点对于平稳窄带随机过程可以很好解释，在平稳窄带随机过程中可认为应力循环的次数等于应力响应正穿越0点的次数；应力峰值分布只与功率谱密度的0阶谱矩有关。对平稳宽带随机过程而言，Dirlik提出的应力幅值概率密度模型与功率谱密度的0、1、2和4阶谱矩都有关，而且单位时间内应力循环正穿越0点的次数小于应力循环的次数。

一般尺度法[6]认为结构在原始载荷下的应力功率谱和强化载荷后的应力功率谱具有相同的谱形状和频率范围，而且使得它们所对应的谱矩具有相同比例关系。由于Dirlik疲劳损伤模型只与0、1、2和4阶谱矩有关，所以结合一般尺度法与Dirlik疲劳损伤模型就可以得到强化载荷前后疲劳寿命之间的强化关系——宽带随机过程下的疲劳强化系数模型。

为了验证疲劳强化系数模型的有效性，需要对悬臂梁分别在原始加速度功率谱和经一般尺度法强化后的加速度功率谱载荷下进行疲劳寿命预测，得到它们的疲劳强化系数。目前对随机振动载荷下结构的疲劳寿命预测已经产生了很多不同的方法。结合雨流计数法[7]（Rainflow counting）和Palmgren-M iner[8]线性累计损伤准则的时域疲劳寿命预测方法凭借其完善的理论基础[9-10]和较好的预测结果[11-12]已经被普遍接受。

本文首先通过有限元分析获得悬臂梁危险点在两种不同载荷下的应力功率谱；接着采用三角级数法对两种不同载荷下应力功率谱进行时域模拟；然后采用雨流计数法（Rainflow counting）和Good-man[13]平均应力修正模型，并结合Palmgren-M iner线性累计损伤准则分别对两种不同载荷下的悬臂梁进行了疲劳寿命预测，得到它们的疲劳强化系数；最后将根据本文提出的疲劳强化系数模型得到的疲劳强化系数和经雨流计数得到的疲劳强化系数进行对比。结果表明：本文提出的平稳宽带随机过程疲劳强化系数模型精度为99.7%，验证了疲劳强化系数模型的有效性。

1 基于一般尺度法的疲劳强化系数模型

为了计算疲劳强化系数，本文首先采用一般尺度法对载荷的加速度功率谱密度进行强化，得到强化之后载荷的加速度功率谱密度与原始载荷的加速度功率谱密度之间的关系，结合有限元理论得到强化载荷下应力响应的功率谱密度与原始载荷下应力响应的功率谱密度之间的关系，计算应力响应谱谱矩之间的关系，最后结合以Dirlik幅值概率密度模型为基础的Dirlik疲劳损伤模型得到强化载荷之后的疲劳寿命和原始载荷下的疲劳寿命之间的关系—疲劳强化系数模型。基本思路如图1所示。

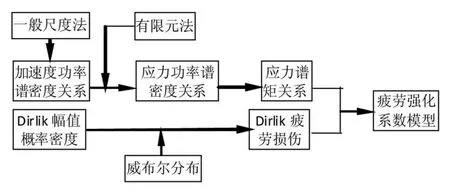
图1 疲劳强化系数模型推导过程

1.1 基本假设

为了得到一个推导相对一致的疲劳损伤，有必要做出一些假设：

(1)材料是线弹性的；

(2)不存在非线性（只有小应力出现）；

(3)随机信号是零均值的稳态高斯分布；

(4)等效应力也满足S-N曲线。

1.2 一般尺度法

将实际条件下的加速度功率谱密度进行简单的线性放大得到试验室条件下的加速度功率谱密度，两者频率范围和形状相同，只是对应频率处幅值进行了相同比例的放大。两者关系如式（1）所示

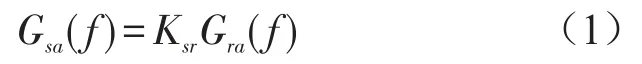
式中Gsa表示试验室条件下的加速度功率谱密度，Gra表示实际条件下的加速度功率谱密度，Ksr表示线性放大系数。

材料承受循环应力是结构产生疲劳失效的重要原因，这些应力必然的带来一定损伤，当损伤达到一定程度就会产生断裂破坏（失效）。因此，必须将外加载荷的加速度功率谱密度转换成应力功率谱密度。

结合有限元基本理论可以推导出结构中每个单元的应力功率谱密度[6]

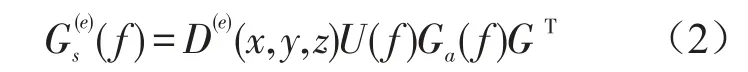
式中上标(e)表示结构中的任意单元，Gs表示应力功率谱密度矩阵，D表示结构的材料和形函数矩阵，U表示结构响应矩阵相关的函数，G表示节点力与节点速度之间的转化矩阵，Ga表示加速度功率谱密度矩阵。

要推导试验条件下的应力功率谱和实际条件下的应力谱之间的关系，还需要做如下假设：

(1)试验测试的结构和实际条件是严格一致的；

(2)试验条件下的约束和实际条件是严格一致的；

在上述假设情况下，联合式（1）和式（2）得到

式中Gss表示试验条件下的应力功率谱密度，Grs表示实际条件下的应力功率谱密度。

定义单侧功率谱密度的谱矩为

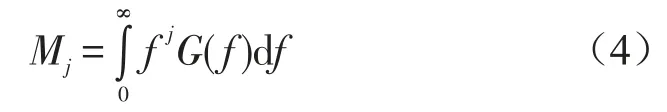
联立式（3）和式（4）可以得到

由上式可知，经过一般尺度法的强化之后，试验条件下的谱矩和实际条件下的对应谱矩也成简单的线性关系。

1.3 Dirlik幅值分布模型

Dirlik通过Monte Carlo技术时域模拟，将宽带平稳随机振动的幅值概率密度由一个指数分布和两个瑞利（Rayleigh）分布的近似[14]

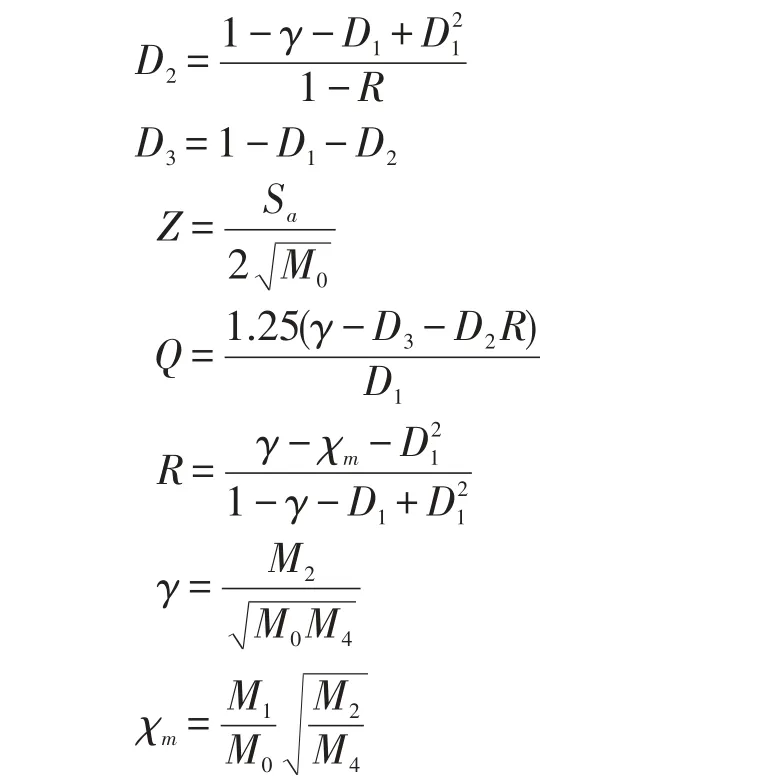
上述Dirlik幅值概率分布模型看似复杂，其实只有四个基本参数即谱矩M0、M1、M2和M4。

1.4 Dirlik疲劳损伤模型

宽带随机分布的损伤模型为

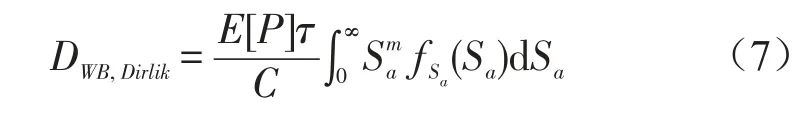
Dirlik疲劳损伤模型为

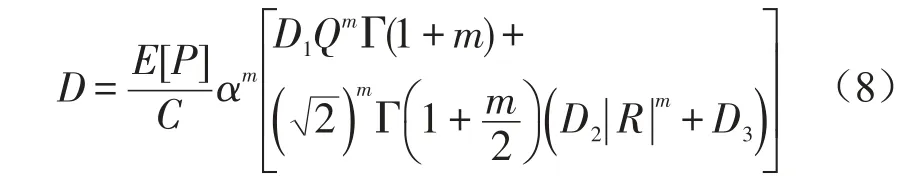
1.5 基于一般尺度法的疲劳强化系数

通过式（5）我们可以知道，式（8）中D1、D2、D3、Q、R和E(P)都不会因为对应力功率谱进行放大而放大。因此，可以简单的得到实际条件下损伤和试验条件下损伤之间的关系为

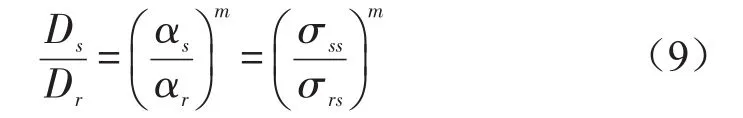
又由式（6）谱矩之间的关系得到

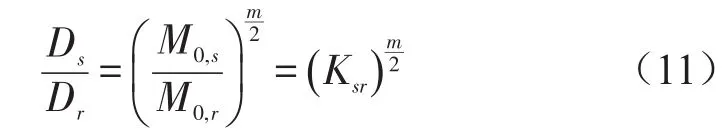
疲劳寿命和损伤之间的倒数关系表示为

因此可以得到疲劳强化系数模型为

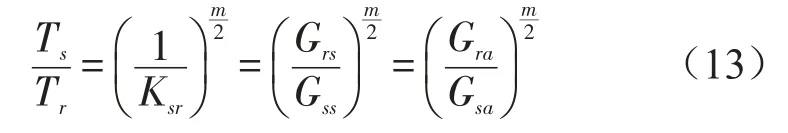
从式（13）中可以看出，本文提出的疲劳强化系数模型只与加速度功率谱线性放大系数以及材料参数m有关。

2 模型验证

为了验证本文提出的宽带随机过程疲劳损伤模型的有效性，首先通过有限元分析获得悬臂梁危险点在两种不同载荷下的应力功率谱。接着采用三角级数法对两种不同载荷下应力功率谱进行时域模拟。然后采用雨流计数法（Rainflow counting）和Good-man平均应力修正模型，并结合Palmgren-M iner线性累计损伤准则对两种不同载荷下的悬臂梁进行疲劳寿命预测，得到它们的疲劳强化系数。最后将经过本文的疲劳强化系数模型得到的疲劳强化系数和经雨流计数方法得到的疲劳强化系数进行对比验证。基本思路如图2所示。

2.1 问题描述

结构尺寸如图3所示的悬臂梁承受来自基座的随机振动，左端固定约束，材料为45钢，右圆孔直径4.1 mm，配重m=2 kg，梁厚度为1 mm，材料参数m=-10.635 6，左端圆孔为激励加载点，载荷方向垂直纸面向上。加载载荷为一恒幅加速度功率谱，频率范围0～200 Hz。其中原始加速度功率谱幅值为，强化加速度功率谱幅值为

图2 疲劳强化系数模型验证过程

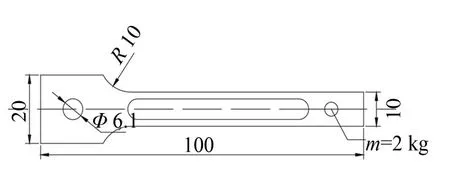
图3 悬臂梁结构示意图（mm）

2.2 振动疲劳分析

首先对悬臂梁进行模态分析，得到其前6阶固有频率分别为2.88 Hz、14.49 Hz、149.23 Hz、1 027.6 Hz、1 057.7 Hz、1 798.4 Hz，随机振动载荷（频率为1～200 Hz）会引起结构共振，采用雨流计数法（Rainflow counting）和Good-man平均应力修正模型，并结合Palmgren-M iner线性累计损伤准则对两种不同载荷进行了疲劳寿命预测。

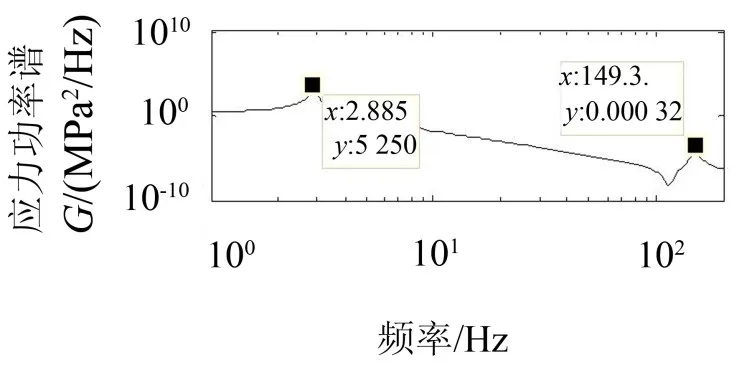
图4-1 原始载荷下的应力功率谱图

2.2.1 确定危险点的应力谱

通过有限元分析可以确定危险部位的位置，并得到危险部位的应力响应功率谱图。如图4-1和图4-2所示，分别为原始载荷的应力功率谱图和强化载荷的应力功率谱图。

2.2.2 应力谱时域模拟

三角级数法也称谐波叠加法，是一种成熟的时域模拟方法，适用于各种谱形随机过程的时域模拟，基本思想是采用离散谱逼近目标随机过程的模拟[15，16]。简谐振动的幅值由随机振动的过程下的均方根值确定，频率取自功率谱密度的频率点，初相位服从0～2π的均匀分布。不断调整初相位，得到一组不同的子样本，计算每个子样本随机过程的不规则因子[1]均值为0.206 6，属于典型的宽带随机过程。

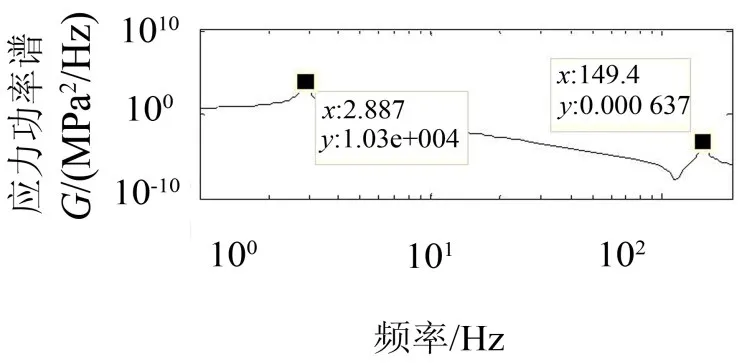
图4-2 强化载荷下的应力功率谱图

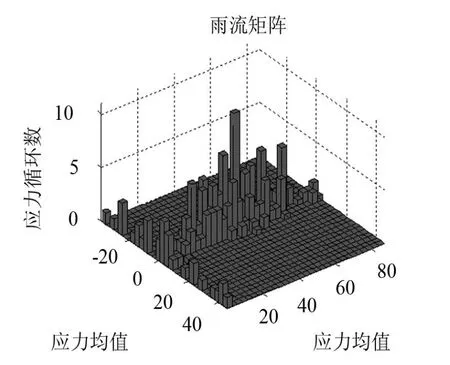
图5-1 原始载荷下的应力雨流计数

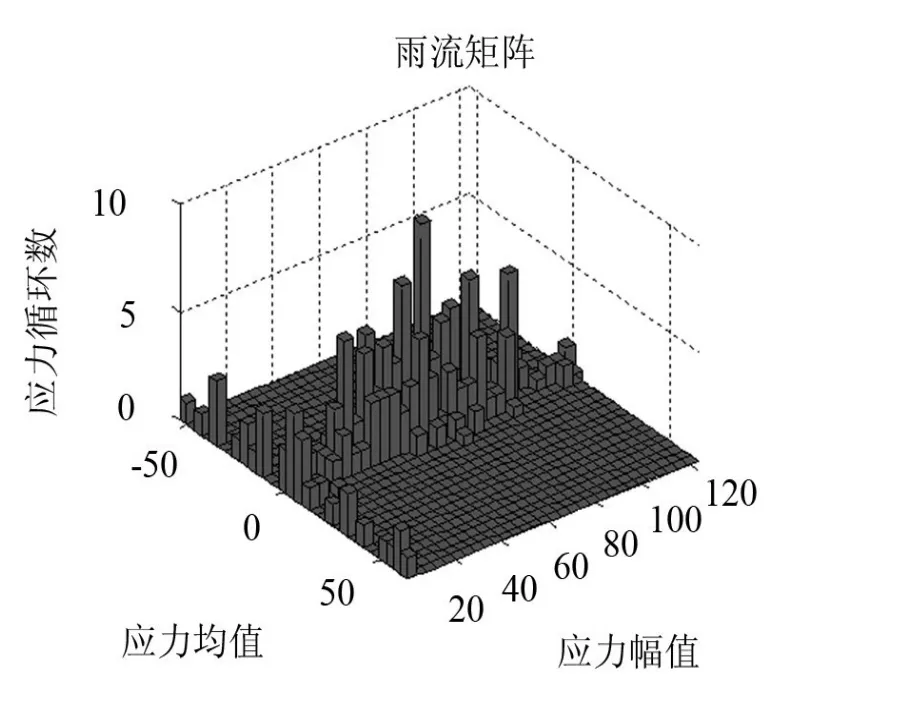
图5-2 载荷强化后的应力雨流计数

2.2.3 雨流计数

将不规则的随机的载荷-时间历程，转化成为一系列循环的方法，称为“循环计数法”。本文采用简单实用且与变幅循环载荷下的应力-应变响应一致的雨流计数法。雨流计数结果如图5-1和图5-2所示。

2.2.4 平均应力修正

平均应力大于零表示拉伸平均应力，S-N曲线下移，表示同样应力幅值作用下的寿命下降，或者说在同样寿命下的疲劳强度降低，对疲劳有不利的影响。平均应力小于零，S-N曲线上移，表示同样应力幅值作用下的寿命增大，或者说在同样寿命下的疲劳强度提高，压缩平均应力对疲劳的影响是有利的。因此，必须对经雨流计数的应力循环进行Good-man平均应力修正。

2.2.5 损伤计算及寿命预测

经过Good-man平均应力修正模型修正后的应力循环，结合Palmgren-M iner线性累计损伤准则得到原始载荷下悬臂梁的疲劳寿命为2.197 3×1010min，强化之后载荷下的疲劳寿命为5.492 6×108min。悬臂梁的疲劳寿命强化40.005倍。

2.3 模型验证

将原始载荷的加速度功率谱和经一般尺度法强化的加速度功率谱幅值代入式（13）得到

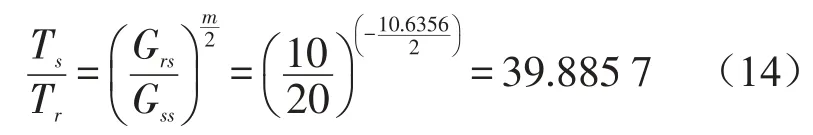
因此，经本文提出的宽带随机振动疲劳强化系数模型计算得到的疲劳强化系数为39.885 7倍，而经雨流计数和M iner损伤准则进行疲劳寿命预测得到的强化系数40.005倍。模型验证表明：本文提出的适用于宽带随机过程的疲劳强化系数模型精度为99.7%，验证了模型的有效性。

3 结语

采用本文提出的适用于宽带随机过程的疲劳强化系数模型进行有关宽带随机过程的加速疲劳试验，只需在知道材料参数m的前提下按照一般尺度法将原始加速度功率谱按照同等比例进行放大作为强化后的加速度功率谱载荷进行疲劳试验。然后结合本文提出的疲劳强化系数模型就可以得到结构在正常载荷下的疲劳寿命。

（1）从模型验证的结果来看，该疲劳强化模型能较好的预测载荷强化之后的疲劳寿命；

（2）疲劳强化系数只与材料的S-N曲线在双对数直线图中的斜率有关；

（3）该疲劳强化系数模型是基于Dirlik模型推导出来的，所以也只适用于平稳高斯信号，并不适合非高斯信号。

[1]张然治.疲劳试验测试分析理论与实践[M].北京：国防工业出版社，2011.44-45.

[2]安刚，龚鑫茂.随机振动环境下结构的疲劳失效分析[J].机械科学与技术，2000，19(9)：40-44.

[3]王长武，张幼安.随机疲劳分析在机载设备疲劳寿命预测中的应用[J].中国机械工程，2004，15（21）：1906-1908.

[4]吴仁智，杨学良，周金华.平地机半轴疲劳寿命预估及其台架疲劳试验[J].中国机械工程，2001，12（12）：1336-1339.

[5]陈沙古，刘荣凤，等.16MnR钢超高周疲劳性能试验[J].西南科技大学学报，2009，24(1)：29-32.

[6]Allegri G,Zhang X.On the inverse power laws for accelerated random fatigue testing[J].International Journal of Fatigue,2008,30:967-977.

[7]Rychlik I A.New definition of the rainflow counting method[J].Int.J.Fatigue,1987,9:119-121.

[8]M iner M A.Cumulative fatigue damage[J].International Journal of Fracture,1945:A159-A164.

[9]Dow ling N E.Fatigue failure prediction of complicated load stress-stain histories[J].ASTM J.Mater,1972,7:71-87.

[10]Wirshing P H,Haugen E B.Probalilistic design for random fatigue loads[J].J.Eng.Mech.Div.ASCE,1973, 99:593-607.

[11]Tovo R.Cycle distribution and fatigue damage under broad-band random loading[J].Int.J.Fatigue,2002,24 (11):1137-1147.

[12]Petrucci G,Zuccarello B.Fatigue life prediction under wide-band random loading[J].Fatigue Fract Eng Mater Struct 2004;27(12):1183-1195.

[13]Sm ith K N,Watson P,Topper T H.A stress-strain function for fatigue of metals[J].Journal of Meterial, 1970,5(4):767-778.

[14]Bishop N W M.The use of frequency domain parameters to predict structural fatigue[D].Ph.D Thesis,Warwick University,1988.

[15]Figwer J.A new method of random time-series simulation [J].Simulation Practice and Theory,1997,5:217-234.

[16]Hu B,Schiehlen W.On the simulation of stochastic process by spectral representation[J].Probabilistic Engineering Mechanics,1997,12(2):105-113.

Analysis of Vibration Fatigue Strength Coefficient Based on General Scaling Law

CHENG Jun-sheng1,YUAN Yi1,YU Zhen-tao2,YUAN Hui2

(1.State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,
Hunan University,Changsha 410082,China; 2.Test Department,Dongfeng Motor Corporation Technical Center,Shiyan 441004,Hubei China）

Based on Dirlik model and combining with the general scaling law,this paper proposes a new model for analyzing the fatigue strength coefficient,which is suitable to the stationary wide-band random vibration loading.The general scaling law considers that the spectral moments of different orders of the stress-response power-spectra of the structure under original loading and strengthened loading have a simple linear relationship.Combination of the spectral moments with the Dirlik wide-band fatigue damage model can lead to the model of the fatigue strength coefficient for the stationary wide-band random vibration loading.To verify the effectiveness of this model,the rainflow counting method and M iner damage criterion are used to predict the fatigue lifespan of a cantilever beam under the original acceleration powerspectral loads.And the result of the fatigue strength coefficient is compared with that calculated by the current model under the present acceleration power-spectral loads strengthened by general scaling law.It is shown that the accuracy rate of the current model of fatigue strength coefficient proposed here can reach 99.7%.Thus,the effectiveness of this model is validated.

vibration and wave;general scaling law;vibration fatigue;fatigue strength coefficient;fatigue life prediction

TB52；V215.5

代码： A

10.3969/j.issn.1006-1335.2014.01.012

1006-1355(2014)01-0047-05

2013-03-13

程军圣(1968-)，男，湖南永州人，湖南大学教授，博士生导师，主要研究方向为：1.动态信号分析与处理；2.机电设备状态监测与故障诊断；3.振动与噪声控制。

E-mail:chengjunsheng_1968@163.com