梁模型三明治板的隔声预报

钱中昌，刘碧龙，刘克

（1.上海市计量测试技术研究院，上海201203；2.中国科学院声学研究所，北京100190）

梁模型三明治板的隔声预报

钱中昌1，2，刘碧龙2，刘克2

（1.上海市计量测试技术研究院，上海201203；2.中国科学院声学研究所，北京100190）

提出一种针对有限大三明治蜂窝板的隔声预报方法。在一定条件下，三明治蜂窝板被看成是正交各向异性的，通过对蜂窝板正交方向上切割下来梁的简单测试，可以得到三明治蜂窝板的等效刚度，结合正交各向异性板的振动方程，把板的振动展开成模态叠加的形式并求解，最终可以得到一块有限大三明治蜂窝板的理论隔声公式，理论预报结果与实验室测量结果对比良好。

声学；三明治板；声传递损失；阻尼；有限大尺寸

三明治结构具有质量轻、刚度大等特性，在多个领域有着重要的应用，其主要原因在于三明治夹层结构普遍具有很高的比刚度。

由于三明治板及加筋板结构的广泛应用，其结构振动特性和隔声性能日益受到人们的重视，国内外学者开展了广泛的研究[1―5]。早在1959年，Kurtze和Watters通过电路类比方法[1]，假定弯曲阻抗和剪切阻抗相互并联得到了复合材料板的总阻抗和结构中传播的弯曲波速度，其结果与弯曲波的理论估计相一致。Dym和Lang[2]把对称三明治板的运动分解为胀缩振动和弯曲振动，分别推导了胀缩振动和弯曲振动模式下板的阻抗并计算了传递系数。Moore和Lyon[3]对具有均质和正交各向异性夹芯的对称无限大夹层复合材料板的声传递特性进行了研究。Narayanan和Shanbhag[4]研究了无限大夹层板的传声损失，研究表明，夹芯的剪切模量对隔声影响尤为显著。国内专门针对蜂窝板隔声问题的研究主要有王胜春等[5]。Nilsson[6]提出了一种三明治梁等效弯曲刚度的估算方法，该方法具有简单易操作等特点。

本文的工作是在Nilsson工作的基础上，得到三明治蜂窝板正交方向上的等效弯曲刚度，结合正交各向异性板的隔声公式，给出有限大三明治蜂窝板的隔声预报方法，并给出了实验验证。

1 三明治板隔声的理论模型

对于本文研究的三明治蜂窝板，在感兴趣的频率范围内（100～4 000 Hz），其振动可以近似为一块正交各向异性的单层板[6]，板的弯曲刚度与频率有关。考虑一块矩形正交各向异性板，尺寸为l1×l2，镶嵌在一块无限大刚性障板上，边界条件为简支，如图1所示。

图1 平面波入射到矩形板示意图

假定入射波为平面波，表示为

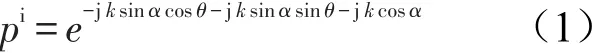
其中α为入射角，θ为入射波在x-y平面投影与x轴的夹角，k是空气中声波波数，板在声波作用下的运动方程可写为

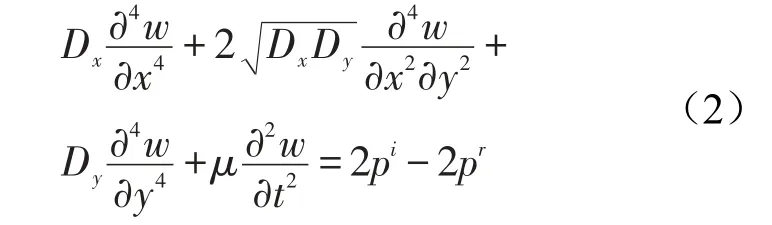
w表示板的法向位移，Dx、Dy分别是x、y方向上的弯曲刚度，pr是板的辐射声压，μ表示板的面密度，这里略去了eiωt以简化计算。

采用模态展开法，把板的位移和声压展开为自由振动模态的叠加，如下

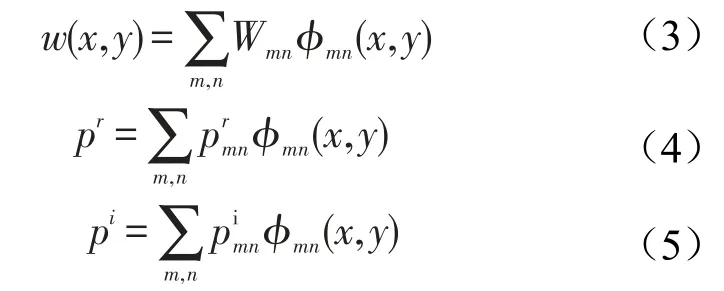
其中φmn(x,y)是归一化基函数，表示为

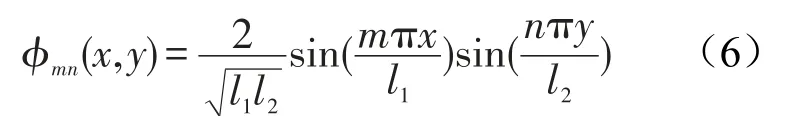
将式（3）至（5）代入（2），利用基函数的正交性，可得

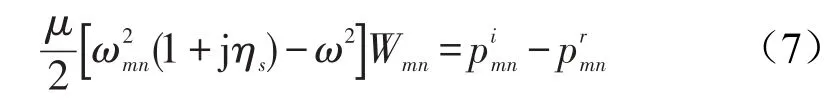
其中ω2mn为

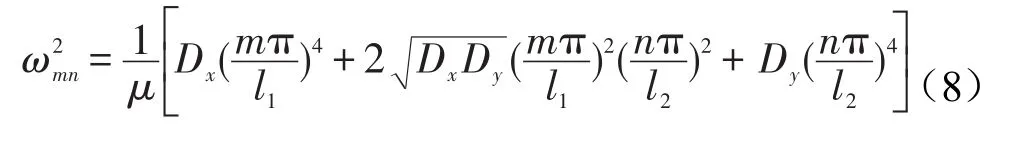
ηs表示结构损耗因子，和可表示成

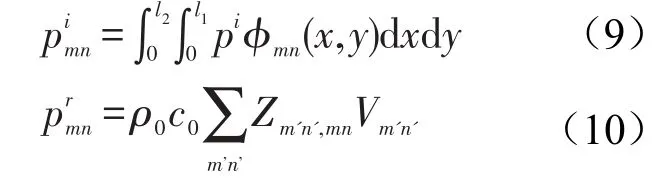
Vm'n'表示板振速的模态分量，Zm,n,,mn是无量纲化的模态阻抗，其实部σm,n,mn也称作模态辐射系数，其虚部相当于在板面上附加一质量块，当空气相对于板为轻流体时，在此处计算隔声时可以忽略。根据文献[7，8],σm,n,mn的非对角项对板的振动和声传递影响甚微，因此σm'n',mn可以简化成σmn，其计算方法可参见[9]，则板的振速响应模态分量可表达为

其中Ymn是模态导纳，表达式为

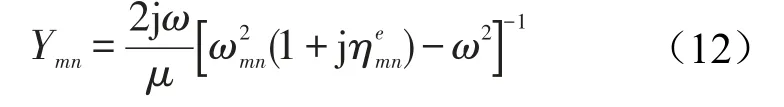
可以看出，有效损耗因子由两部分组成，一部分是结构本身固有的损耗，另一部分则是由于辐射引起的损耗。入射到整个板的声功率为Ji=l1l2cosα/2ρ0c0，透射的声功率为

整个板的声透射系数可表达成

上式表示的是某单一角度平面波入射时的声传递损失，对于扩散场声波入射，可以采用Fahy[10]文献中提到的公式，把单一角度声透射推广到整个扩散场的透射，具体形式为

上式中运用了一个重要的关系式，如下

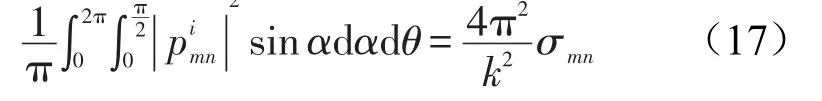
进一步可以得到声传递损失

2 正交方向上等效刚度的测量

用于实验测量的两块三明治板参数如表1所示，两块板包括面板和夹芯都由铝压制而成。

如图2所示，Beam Ax和Ay是从板A上沿x和y方向切割下来的两根梁，板B与此类似。把切割下来的梁用弹性绳悬挂于钢架上，用力锤敲击梁上任一部位，并用加速度计测出梁上各点的速度响应，分别改变敲击的部位和加速度计的测点以避免遗漏测点，最终可测得梁在两端自由边界条件下前几阶的共振频率。根据上文提到的Nilsson的工作，把测量所得前几阶频率代入到下式[6]

表1 测试用蜂窝板尺寸

图2 蜂窝梁的割取示意图

上式中Dxn表示第n阶模态的弯曲刚度，fn对应其共振频率，μ为梁单位面积质量，L是梁的长度，αn的取值参见文献[6]。由此可见，通过简单的模态实验便可获得梁在共振频率处的等效弯曲刚度，对于其它频率，弯曲刚度满足式下式

其中

上式中，D2为两层薄面板的弯曲刚度，蜂窝夹芯的有效剪切模量为Ge，D1为梁的静态弯曲刚度。根据所测得的各阶共振频率处的等效弯曲刚度，利用最小二乘法，便可拟合得出参数A，B和C，再代入式（20），便可得到各个频率处的弯曲刚度。拟合时，选取的目标函数定义为

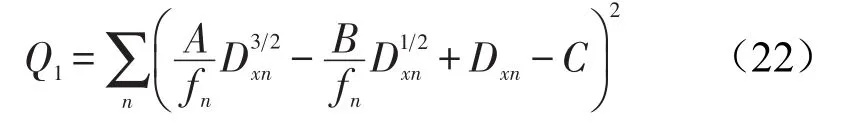
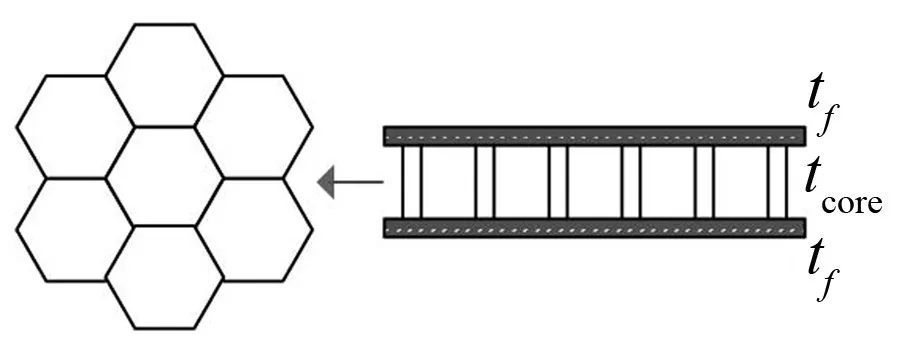
图3 蜂窝板剖面示意图

拟合结果如图4和5所示，观察可发现，蜂窝板的等效弯曲刚度随频率增大而减小，最终趋于一常数。同时还可以发现，三明治蜂窝板存在很强的各向异性，且随着频率的增加这种差别逐渐变大。

表2 梁的基本参数

图4 蜂窝板A的动态弯曲刚度

图5 蜂窝板B的动态弯曲刚度

3 实验验证

为了验证理论的正确性，两块板的隔声量通过专用隔声室测量，隔声室由声源室和接收室构成，在两室之间的隔断墙壁上，有一1.08 m×1.20 m的开口，测试板被安装在其中，如图6和7所示，整个测试参照国家标准[11]。隔声量表示为

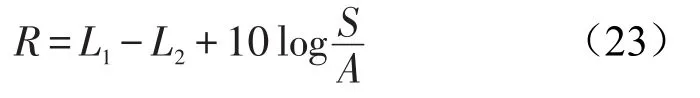
其中L1和L2分别是声源室和接收室的平均声压级。S和A分别是试件的面积和接收室的总吸声量，其中V是接收室体积，T60表示接收室的混响时间。

图6 声源室照片

图7 接收室照片

图8和9给出了两块板的测试结果，并给出了和理论结果的对比。

图8 结果与实验对比（A板）

图9 结果与实验对比（B板）

理论预报时，阻尼损耗因子取1%，可以发现，实验结果和理论预报结果基本吻合。在低频段，理论结果与实验结果存在一些差异，这主要是由于边界条件不确定性造成的，理论模型是基于简支边界条件的，而实际边界条件是介于简支和固支之间的，边界对声传递的影响主要在低频段。理论预报和实验结果另一处差异出现在吻合频率附近，这一频段内，理论预报隔声量低于实验值，导致这一结果的原因可能是理论计算所用的阻尼损耗因子低于实际值。

4 结语

本文在前人工作的基础上，提出了一种用于预报三明治蜂窝板隔声的方法，该方法基于三明治梁的理论，在一定频率范围内，把蜂窝板等效成一块正交各向异性单层板，板的弯曲刚度可以通过简单的模态实验得到。理论预测结果与实验测得结果对比良好。

[1]Kurtze G and Watters B.New wall design for high transm ission loss or high damping[J].Journal of Acoustical Society of America,1959,31:739-748.

[2]Dym C L and Lang M A.Transmission of sound through sandwich panels[J].Journal of the Acoustical Society of America ,1974,56:1523-1532.

[3]Moore J A and Lyon R H.Sound transmission loss characteristics of sandwich panel constructions[J].Journal of the Acoustical Society of America ,1991,89:777-791.

[4]Narayanan S and Shanbhag R L.Sound transmission through a damped sandwich panel[J].Journal of Sound and Vibration,1982,8 0:315-327.

[5]WANG Sheng-chun,DENG Zhao-xiang,SHEN Wei-dong.Sound transmission loss characteristics of unbounded orthotropic sandwich panels in bending vibration considering transverse shear deformation[J].Composite Structures,2010,92:2885-2889.

[6]Nilsson E,Nilsson A C.Prediction and measurement of some dynam ic properties of sandwich structures with honeycomb and foam cores[J].Journal of Sound and Vibration,2002,251:409-430.

[7]Takahashi D.Effects of panel boundedness on sound transm ission problems[J].Journal of the Acoustical Society of America,1995,98:2598-2606.

[8]Li W L and Gibeling H J.Determ ination of the mutual radiation efficiencies of a rectangular panel and their impact on the radiated sound power[J].Journal of Sound and Vibration,2000,229:1213-1233.

[9]Wallace C E.The acoustic radiation damping of the modes a rectangular panel[J].Journal of Acoustical Society of America,1987,81:1787-1794.

[10]Fahy F.Sound and structural vibration:radiation, transmission and response[M].Academic Press,London, 2007.

[11]GB/T 19889.3-2005.建筑和建筑构件隔声测量.第3部分：建筑构件空气声隔声的实验室测量[S].

Prediction of Sound Transm ission Loss for Sandwich Panel by Using Beam Model

QIAN Zhong-chang1,2,LIU Bi-long2,LIU Ke2

(1.Shanghai institute of Measurement and Testing Technology,Shanghai 201203,China; 2.Institute ofAcoustics,ChineseAcademy of Sciences,Beijing 100190,China)

An approach for prediction of sound transm ission loss for a finite sandwich panel with honeycomb core is described.The sandwich panel is treated as an orthotropic structure,which bending stiffness in two principal directions is estimated by means of simple tests on beam elements isolated from the sandwich panel.Utilizing orthotropic panel theory, along with the obtained bending stiffness in two directions,the sound transm ission loss of simply-supported sandwich panel is predicted by modal expansion method.The predicted transm ission loss is compared with the measurement data and their agreement is good.

acoustics;sandwich panel;sound transmission loss;damping;finite size

TB5

A

10.3969/j.issn.1006-1335.2014.01.003

1006-1355(2014)01-0012-04

2013-03-14

国家重点基础研究发展计划(973计划基金编号：2012CB720204)

钱中昌（1986-），男，江苏南通人，博士，目前从事机舱噪声研究。

E-mail:qianzhongchang@mail.ioa.ac.cn