动载荷识别时域方法的研究现状与发展趋势
2014-07-25周盼张权率志君李玩幽
周盼,张权,率志君,李玩幽
(哈尔滨工程大学动力与能源工程学院,哈尔滨150001)
动载荷识别时域方法的研究现状与发展趋势
周盼,张权,率志君,李玩幽
(哈尔滨工程大学动力与能源工程学院,哈尔滨150001)
与动态载荷识别的频域方法相比,时域方法不仅适用于线性系统,还适用于非线性系统以及能有效处理瞬态冲击激励的识别问题,近年来时域方法愈发受到学者们的关注。目前广泛应用的几种时域方法主要有—反卷积法、计权加速度法、函数逼近法、卡尔曼滤波器和递归最小二乘法、逆系统法以及新兴的智能方法等等。在对各方法研究现状的概述与总结中,分析了各自的优缺点。从研究对象、研究方法、应用领域三方面分析,非线性系统、线性时变系统将成为分析研究的重点。结论显示,与现代智能算法相结合的逆系统方法将成为新的研究热点,将其相应的载荷识别方法应用于机械设备的故障诊断也将成为今后发展的新趋势。
振动与波;载荷识别;逆问题;时域识别方法;综述
在工程结构设计、试验及性能研究中,研究人员为分析结构的动态特性,进行结构动力响应计算、动态参数设计、故障分析及可靠性预测等,往往需要精确掌握作用在结构上的动态载荷。因此,如何确定结构的动态载荷已成为工程实际中迫切需要解决的一个问题。
载荷识别是结构动力学的第二类反问题,是根据结构动态特性和实测动态响应估计结构所受到的动态载荷[1]。近年来,不少国内外学者对载荷识别的研究进展进行了总结分析[2―4]。文献[4]对频域识别方法做了比较全面的归纳总结。在频域内,系统输入激励与输出响应之间表现为线性关系。载荷识别只需要对系统特性矩阵作逆运算即可,容易实现。但是频域法需要对测试信号进行傅里叶变换,要求信号样本具有一定的长度,所以频域法一般只适用于稳态动载荷或随机载荷,不适用于冲击载荷的识别[3]。此外,系统的频率响应函数矩阵在共振频率附近一般呈现病态,导致载荷识别误差很大。频域方法是基于系统线性假设的,并不能识别非线性系统的载荷。
与频域法相比,时域方法不需要对采集信号作傅里叶变换,识别精度不受信号采集方式的影响[3]。此外,时域识别方法能够处理瞬态冲击载荷。且对于非线性系统,时域方法更有其优势。
本文主要对近年来载荷识别的时域方法进行总结分析,具体包括反卷积方法、计权加速度法、函数拟合法、卡尔曼滤波器和递归最小二乘法、逆系统法,希望为以后的研究提供一定的借鉴和参考价值。
1 反卷积方法
时域内动载荷与系统响应(包括位移、速度、加速度、应变)之间表现为复杂的卷积关系,如式(1)所示。

在数学上,载荷识别就是反卷积过程。反卷积方法可以归纳为三类:时域反卷积[5,6]、频域反卷积[7-―11]和小波反卷积[12,13]。
1.1 时域反卷积
1998年,Wu利用应变重构冲击载荷的时间历程,对比了梯度投影法和相位变换法的识别精度,结果表明梯度投影法稳定性更好,对噪声更不敏感[5]。
2008年,Kazem i提出利用应变的时间积分识别动态载荷,识别结果表明:采用应变识别的载荷波动很大,需要采用正则化方法,且识别载荷对测试噪声很敏感。利用应变第三时间积分求解的载荷精度很高,无需应用正则化,且其对测试噪声和传感器位置均不敏感,识别结果很稳定[6]。
1.2 频域反卷积
频域反卷积是首先将响应信号进行傅里叶变换,在频域内进行载荷的求解,然后将频域识别载荷进行傅立叶逆变换得载荷的时间历程。
对于频域反卷积法,频率响应函数是必需的,应尽量保证频响函数的测试精度。1991年,针对图1中输入输出模型,Inoue对比了估计频响函数的五种不同方法,然后识别冲击载荷,结果表明:采用H4,H5估计频响函数时对噪声不敏感,载荷识别精度较高[7]。
x(t),y(t)为实测输入及输出(包含噪声)
f(t),e(t)为真实输入及输出;m(t),n(t)为输入及输出噪声

图1 输入激励输出响应模型

频域反卷积方法需要对频响矩阵求逆,可能会由于矩阵病态导致运算失效。为避免频响矩阵求逆,1997年,傅志方等人对单输入单输出系统采用非因果维纳滤波器理论获得最优逆系统的频响函数2000年,饶柱石等研究了多输入多输出系统的优化逆系统的频响矩阵[9]。基于优化逆系统的载荷识别方法抗噪声干扰能力良好,尤其当测量信号受到较严重的噪声污染时,明显优于传统方法。
此外,Inoue研究了快速傅里叶变换中窗函数对载荷识别的影响,指出:若采用矩形窗对响应信号进行傅里叶变换,其识别载荷精度差,应采用指数窗,相当于Laplace变换,且衰减系数为是比较合理的[10]。
基于傅里叶变换的频域反卷积方法,优点是频率具有对应性即激励与响应的频率关系是一一对应的[12]。但是频域反卷积方法是以傅里叶变换为基础的,因此为保证载荷识别精度需要较长的时间窗。此外在某些频率下由于反射波的相互干扰会导致响应信息的丢失,导致频域反卷积方法失效,Martin和Doyle对此问题进行了研究[11]。采用多点组合识别载荷可以弥补响应信息丢失的影响;此外,通过给系统频率响应函数添加噪声也可以缓解信息丢失的问题[12]。
1.3 小波反卷积
针对频域反卷积法不能有效处理响应中存在反射波的问题,1997年,Doyle采用小波反卷积的方法识别作用于梁和板结构的冲击载荷[12]。Doyle采用光滑的三角波函数作为基函数,则频响矩阵是对称Toeplitz矩阵,极大地降低计算量。
2008年,程良彦等人采用小波反卷积方法对拱结构的冲击激励进行实验研究。识别载荷与实测载荷整体吻合很好,但冲击激励的上升沿、下降沿识别结果较差,这是由于小波的紧支性构造的数据较离散造成的[13]。
小波反卷积法的优势在于不受结构中反射波的影响,并且与有限元技术结合可以分析复杂结构的载荷识别问题。然而,在选择脉冲宽度、项数目、时间长度、平移量等参数时需要一定的经验。
2 计权加速度法
计权加速度法(Sum of Weighted Acceleration Technique,SWAT)是一种基于模态滤波器的方法,由结构的刚体模态和关心频率下的弹性模态组成一组模态滤波器,提取出结构的刚体运动响应,再根据结构的质量特性确定结构的刚体运动载荷。
1987年,Kreitinger等人提出了适用于自由系统的计权加速度方法[14]。动载荷由测试加速度x¨i() t与有效计权wi的乘积来估计

式(3)中n为系统自由度数目,有效计权wi是指每个测点的等效质量系数。它适用于具有刚体振型的实际结构,但识别精度取决于加速度的测试位置与加权系数的选取。其后,将该方法应用于非线性系统的载荷识别中。
1999年,路敦勇和吴淼[15]将SWAT推广到约束系统的等效外载荷识别中,并采用递推最小二乘法确定加权系数。等效外载荷的计算公式如式(4)示,式中fk(t),fc(t)分别为约束系统受到的弹簧力和阻尼力。

2002年,陈莲采用有限元方法获得结构的振型函数,然后求解有效计权,对悬臂梁进行了载荷识别的数值仿真研究[16]。结果说明:即使在缺省模态下,采用该方法也可以较精确地识别动态载荷。对于n自由度结构,采用n-6阶模态即可计算出有效计数。
SWAT方法能够识别稳态载荷与冲击载荷,但仅适用于具有刚体模态的结构且所求为动态载荷的合力,故其应用有很大的局限性。此外,该方法要求测量传感器的数目至少等于刚体模态和关心频率下弹性模态的数目之和,同时要求加速度传感器的配置要合理,确保得到的滤波器具有较好的计算性能。
3 函数拟合法
函数拟合法,是通过函数的线性组合表示动载荷,如式(5),将载荷识别问题转化为权系数的求解问题,从而简化载荷与响应之间复杂的卷积关系。

式(14)中ci为未知权系数,φi()t为展开函数或基函数,这些函数可以是幂级数、正交多项式、样条函数等。对于精确解,式(14)是无穷项之和,对于近似解,则是有限项之和。
1996—1998年,张方等人先后采用幂级数、广义正交多项式作为基函数拟合系统响应和载荷[17—19]。幂级数存在收敛性差、稳定性差的缺点。广义正交多项式法能够用于冲击载荷的识别,但是多项式阶数随模态增加而增加,导致计算量迅速增加。
2003年,王彦卫等人采用光滑样条函数拟合位移响应,然后根据N自由度粘性阻尼系统的振动微分方程直接求解系统载荷[20]。
2006年,Gunawan等人采用两步B样条函数正则化方法重构动态载荷的时间历程[21]。首先选取使目标函数最小的节点个数以确定冲击激励的加载和卸载过程,然后重新确定加载过程的最优节点数目,采用B样条函数拟合冲击激励,通过求解权系数识别冲击激励。
2007年,Hu N采用切比雪夫多项式拟合时域冲击激励,以估计应变与测试应变的平方误差最小为目标函数,采用二次规划法求解多项式的权系数,从而识别结构载荷[22]。同时,Hu N对载荷位置识别进行了研究。
2007年,秦远田采用矩量法基函数拟合未知动载荷[23]。此外,秦远田对拟合阶数进行了研究,表明:只有当基函数的主频率略大于待识别载荷的最高频率时,才能获得很好的拟合精度。
2008年,Gunawan等人采用正则化二次样条函数拟合冲击载荷,利用基于L曲线的TSVD方法求解载荷[24]。该方法能够提供比较精确的载荷识别结果,但是不能精确识别冲击载荷的卸载过程(幅值为0)。
2009年,史红霞采用广义切比雪夫正交多项式拟合模态载荷函数,结合Duhamel积分方程识别系统的模态载荷,然后通过模态坐标变换求解动态载荷[25]。该方法不能识别含白噪声的谐载荷。此外,由于载荷识别过程中采用的是递归连锁计算格式,容易产生误差积累。
4 卡尔曼滤波器和递归最小二乘法
卡尔曼滤波器(Kalman filter)属于现代控制理论,现已成功应用于动载荷的识别问题中。下面对卡尔曼滤波器和递归最小二乘法(Recursive Least Square,RLS)进行介绍。
n自由度线性系统的离散状态空间模型

式(6)中状态向量X(k)=[x(k) x˙(k)]T,F(k)=[0n×nf(k)]T,观测向量Z(k)=x(k)。x(k),f(k)分别为n×1阶位移响应向量、输入激励向量。Φ为状态转移矩阵,Γ为输入矩阵。w(k),v(k)分别过程噪声、测试噪声向量。
卡尔曼滤波器方程为
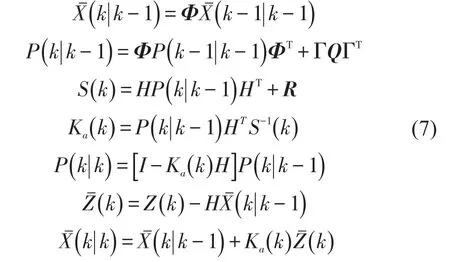
递归最小二乘法的相关方程表述为

式(8)中γ为权系数,Bs(k)和Ms(k)为灵敏度矩阵,Kb(k)为更新的修正增益,Pb为估计激励的误差协方差,为估计激励。
针对卡尔曼滤波器和递归最小二乘法,国外学者提出了三种不同权系数应用于载荷识别问题,分别是常权系数[26―32]、自适应权系数[33―35]、智能模糊权系数[36―39]。
M.H.Lee采用三种不同权系数识别激励,发现:智能模糊权收敛性更好,能有效降低测试误差、模型误差、仪器造成的测试偏差对识别结果的不良影响,并且跟踪能力好[36]。此外,D.C.Lin也验证了自适应权系数较常权系数的载荷精度要高[35]。
为将该方法从线性系统推广到非线性系统,研究学者引入了广义卡尔曼滤波器(Extended Kalman Filter,EKF)。广义卡尔曼滤波器的基本思想是,在最近一次状态估计的每一时刻,将非线性状态空间模型进行线性化处理,然后再应用标准卡尔曼滤波器方程[40]。2004年,Ma和Ho采用EKF和RLS在线识别非线性集中质量系统的时域载荷[33]。2010年,Lin采用EKF和RLS对单自由度非线性系统进行外载荷的数值仿真研究[32]。
卡尔曼滤波器和RLS是以系统的状态空间模型为基础的,能够在线识别未知载荷的时间历程,节省时间,减小计算机负荷。此外,采用该方法需要了解测试噪声及过程噪声的统计特性,其对识别精度有影响。该方法能够较准确地估计正弦激励和冲击激励,但是对于连续冲击激励,该方法只能完全跟踪第一个冲击。
5 逆系统方法
鉴于频响矩阵求逆过程中可能出现的病态问题,1995年,魏星原等采用逆系统法提高载荷识别精度[41]。该方法利用系统的输入输出信息建立自回归滑动平均(ARMA)逆模型,然后求解输入激励,从而将载荷识别的逆问题转化为正问题进行处理。
线性常系数系统的离散状态方程为

式(9)中X(k+1)为系统状态向量,F(k)为系统输入向量,A,B,C,D分别为系统矩阵、控制矩阵、输出矩阵和直接传递矩阵。
线性系统在满足可逆、稳定、能控、能观四个条件下,逆系统状态方程为

其中

但是由于逆系统的存在条件比较苛刻,这种方法的应用受到一定的限制。
1999年,Steltzner和Kammer提出采用非因果逆向结构滤波器(Inverse Structural Filter,ISF)识别结构所受激励[42]。采用TSVD方法求解由Markov参数构成的结构特性矩阵的伪逆,即可得到结构的逆向滤波器(其中引入了延迟)。但是受测试噪声的影响,ISF的系统矩阵的奇异性会导致载荷识别结果不稳定。
2004年,Nordström等人采用时延方法将载荷识别的不适定问题转化为适定问题,研究了时间延迟对激励力识别精度的影响[43]。
针对ISF受测试噪声影响会产生不稳定结果的缺点,2008年,Allen和Carne提出一种延迟逆向滤波器算法计算系统的外部激励[44]。
6 载荷识别的新方法
由于计算机技术的发展以及实际工程需要,国内外学者将一些新算法引入到动态载荷识别领域,如小波正交算子变换法[45,46]、遗传算法[47,48]、神经网络算法[49―52]。
杨萍等人引入离散正交小波,有效提取高阶模态信息,克服窗口FFT对时频局部无法调节的缺点,提高了载荷识别精度[46]。严刚将冲击力等效为一系列参数,以计算值与测试值误差为目标函数,采用遗传算法调整参数,从而识别冲击力的位置和时间历程[47]。张方等人采用神经网络算法建立了动载荷识别模型,该方法精度高,无累积误差,抗干扰能力强,对冲击载荷的识别更具独特优势[49]。
7 发展趋势分析
动态载荷识别为结构的动态计算、设计及分析提供可靠的依据,动态载荷识别对工程应用意义重大,其研究正在蓬勃发展。从载荷识别的研究对象、研究方法、应用领域三方面进行发展趋势分析。
实际机械系统中大量存在非线性特性,这增加了载荷识别的困难。目前较多的工作还是针对线性系统展开的,也有学者已经对非线性结构的载荷识别展开研究。研究复杂结构的非线性系统理论模型和方法是今后发展的方向之一。大多数载荷识别问题是对线性时不变系统展开研究的,即系统的特征参数与时间无关。对线性时变系统,频响函数测试时系统状态与响应测试时系统状态不一致,会导致载荷识别很难取得理想的结果。因此针对线性时变系统还需要发展动载荷的在线识别技术。
通过分析几种时域方法的优劣,不难发现逆系统方法结合现代控制理论中的智能算法是未来研究的热点之一。在上述几种方法中,逆系统方法原理简单,便于理解。但是目前的逆系统方法是建立在系统状态空间模型的基础上的,需要提前掌握系统的先验知识。在只能获取系统输入输出信息的情况下,建立系统的准确逆模型是非常重要的。引入新兴的智能算法,可有效建立系统的逆模型。对于简单的线性系统,可采用一组权向量模拟逆系统。复杂系统可采用神经网络方法进行逆向建模。此外,借鉴现代控制理论中广泛应用的支持向量机,无论是线性系统还是非线性系统的载荷识别问题,均能进行有效处理。
将载荷识别应用于机械设备的故障诊断中是未来发展的一个重要方向。目前工程中故障诊断多采用振动响应进行判定,无论是从时域、频域、幅值域、时频域,均得到了长足的发展。但是并未从根本上分析系统的力源特性。响应体现的不仅仅是力源特性,其中还包含了系统振动传递路径的信息。从力源角度分析故障,就是将系统传递路径剥离出来。例如,对往复运转机械,采用扭振识别不同运转状态下的激励力,识别故障状态。通过载荷识别分析激励源特性从而诊断机械设备的故障,是故障诊断技术未来发展的新趋势。
[1]傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000.
[2]Inoue H,Harrigan J J,Reid S R.Review of inverse analysis for indirect measurement of impact force[J].Appl Mech Rev,2001,54(6):503-524.
[3]许锋,陈怀海,鲍明.机械振动载荷识别研究的现状与未来[J].中国机械工程,2002,13(6):526-531.
[4]胡寅寅,率志君,李玩幽,刘志刚.设备载荷识别与激励源特性的研究现状[J].噪声与振动控制,2011(4):1-5.
[5]Wu E,Tsai C Z and Tseng L H.A deconvolution method for force reconstruction in rods under axial impact[J].J.Acoust.Soc.Am.,1998,104(3):1418-1426.
[6]Kazem i M,Hematiyan M R,Ghavam i K.An efficient method for dynam ic load identification based on structural response[C].EngOpt 2008-International Conference on Engineering Optim ization.Rio de Janeiro,Brazil,2008:1-5.
[7]Inoue H,Ishida H,Kishimoto K,Shibuya T.Measurement of impact load by using an inverse analysis technique (Comparison of methods for estimating the transfer function and its application to the instructed charpy impact test)[J].JSME International Journal,1991,34(4):453-458.
[8]傅志方,饶柱石,周海亭.一种动态载荷的识别方法[J].上海交通大学学报,1997,31(3):5-7.
[9]饶柱石,施勤忠,荻原一郎.基于逆系统分析法的多输入多输出的动载荷优化估计[J].振动与冲击,2000,19 (2):8-12.
[10]Inoue H,Ikeda N,Kishimoto K,Shibuya T and Koizumi T.Inverse analysis of the magnitude and direction of impact force[J].JSME Int.J.,1995,38(1):84-91.
[11]Martin M T,Doyle J F.Impact force identification from wave propagation responses[J].Int.J.Impact Eng.,1996, 18(1):65-77.
[12]Doyle J F.A wavelet deconvolution method for impact force identification[J].Experimental Mechanics,1997,37 (4):403-408.
[13]程良彦,宋振华,王志华,马宏伟.基于小波反卷积的冲击力识别[J].暨南大学学报(自然科学版),2008,29 (5):443-446.
[14]Kreitinger T,Luo H L.Force identification from structural responses[C].Proceedings of the 1987 SEM spring conference.June 1987:851-855.
[15]路敦勇,吴淼.动态载荷识别的SWAT方法研究[J].振动与冲击,1999,18(4):78-82.
[16]陈莲,周海亭.动态载荷识别的计权加速度法[J].噪声与振动控制,2002(3):14-16.
[17]张方,朱德懋.动态载荷时域识别的级数方法[J].振动工程学报,1996,9(1):1-8.
[18]张方,朱德懋.基于广义正交域的一种动载荷识别方法研究[J].南京航空航天大学学报,1996,28(6):755-760.
[19]张方,朱德懋,张福祥.动载荷识别的时间有限元模型理论及其应用[J].振动与冲击,1998,17(2):1-5.
[20]王彦卫,赵玫.一种新的动态载荷识别方法[J].噪声与振动控制,2003(3):11-13.
[21]Gunawan F E,Homma H,Kanto Y.Two-step B-splines regularization method for solving an ill-posed problem of impact-force reconstruction[J].Journal of Sound and Vibration,2006,297:200-214.
[22]Hu N,Fukunaga H,Matsumoto S,Yan B,Peng X H.An efficient approach for identifying impact force using embedded piezoelectric sensors[J].International Journal of Impact Engineering,2007,34:1258-1271.
[23]秦远田.动载荷识别应用技术研究[D].南京:南京航空航天大学博士学位论文,2007.
[24]Gunawan F E,Homma H and Morisawa Y.Impact force estimation by quadratic spline approximation[J].Journal of Solid Mechanics and Materials Engineering,2008,2 (8):1092-1103.
[25]史红霞.基于修正广义正交域的动载荷识别研究[D].哈尔滨:哈尔滨工业大学硕士学位论文,2009.
[26]Ma C K,Tuan P C,Lin D C and Liu C S.A study of an inverse method for the estimation of impulsive loads[J].International Journal of Systems Science,1998,29(6): 663-672.
[27]Ma C K,Lin D C,Chang J M.Estimation of forces generated by a machine mounted upon isolators under operating conditions[J].Journal of the Franklin Institute, 1999,336:875-892.
[28]Ma C K,Lin D C.Input forces estimation of a cantilever beam[J].Inverse Problem in Engineering,2000,8(6): 511-528.
[29]Ma C K,Chang J M,Lin D C.Input forces estimation of beam structures by an inverse method[J].Journal of Sound and Vibration,2003,259(2):387-407.
[30]Liu J J,Ma C K,Kung I C,Lin D C.Input force estimation of a cantilever plate by using a system identification technique[J].Computer Methods in Applied Mechanics and Engineering,2000,190:1309-1322.
[31]Wu A L,Loh C H.Input force estimation using system identification techniques[C].8 th Pacific Conference on Earthquake Engineering,2007.
[32]Lin D C.Input estimation for nonlinear systems[J].Inverse Problems in Science and Engineering,2010,18 (5):673-689.
[33]Ma C K,Ho C C.An inverse method for the estimation of input forces acting on non-linear structural systems[J].Journal of Sound and Vibration,2004,275:953-971.
[34]Chen T C and Lee M H.Determ ination of moving tank and missile impact forces on a bridge structure[J].Defence Science Journal,2008,58(6):752-761.
[35]Lin D C.Adaptive weighting input estimation for nonlinear systems[J].International Journal of Systems Science,2012,43(1):31-40.
[36]Lee M H.Intelligent fuzzy weighted input estimation method for the input force on the plate structure[J].Structural Engineering and Mechanics,2010,34,(1):1-14.
[37]Lee M H,Chen T C.Intelligent fuzzy weighted input estimation method for the forces generated by an operating rotating machine[J].Measurement,2011,44 (5):917-926.
[38]Lee M.H,Chen T.C,Yu T P and Jang H Y.The study of the intelligent fuzzy weighted input estimation method combined with the experiment verification for the multilayer materials[J].World Academy of Science, Engineering and Technology,2009,53:113-122.
[39]Lourens E,Reynders E,Roeck G D,Degrande G, Lombaert G.An augmented Kalman filter for force identification in structural dynam ics[J].Mechanical Systems and Signal Processing,2012,27:446-460.
[40]Simon Haykin著,郑宝玉,等译.自适应滤波器原理(第四版)[M].北京:电子工业出版社,2003.
[41]魏星原,宋斌,郑效忠.载荷识别的逆系统方法[J].振动、测试与诊断,1995,15(3):37-43.
[42]Steltzner A D.Input force estimation,inverse structural system and the inverse structural filter[D].The University of Wisconsin-Madison,Ph.D thesis,1999.
[43]Nordström L J L,Nordberg T P.A time delay method to solve non-collocated input estimation problems[J].Mechanical Systems and Signal Processing,2004,18: 1469-1483.
[44]Allen M S,Carne T G.Delayed multi-step inverse structural filter for robust force identification[J].Mechanical Systems and Signal Processing,2008,22: 1036-1054.
[45]赵玉成,袁树清,李舜酩,等.动态载荷的小波正交算子变换识别法[J].机械强度,1998,20(2):127-130.
[46]杨萍,李鹤岐,李有堂.动态载荷识别的小波正交算子变换法[J].甘肃工业大学学报,2001,27(2):102-105.
[47]Yan G,Zhou L.Impact load identification of composite structure using genetic algorithms[J].Journal of Sound and Vibration,2009,319:869-884.
[48]Hashem i R and Kargarnovin M H.Vibration base identification of impact force using genetic algorithm[J].International Journal of Mechanical Systems Science and Engineering,2007,1(4):204-210.
[49]张方,朱德懋.基于神经网络模型的动载荷识别[J].振动工程学报,1997,10(2):156-162.
[50]Williams M E,Hoit M I.Bridge pier live load analysis using neural networks[J].Advances in Engineering Software,2004,35:645-652.
[51]田燕,邢士勇,张志斌,郑海起.基于径向基网络的变速箱载荷识别研究[J].振动、测试与诊断,2004,24 (2):100-102.
[52]赵凤遥.水电站厂房结构及水利机械动力反分析[D].大连:大连理工大学博士学位论文,2006.
Review of Research and Development Status of Dynam ic Load Identification in Time Domain
ZHOU Pan,ZHANG Quan,SHUAI Zhi-jun,LI Wan-you
(College of Power and Energy Engineering,Harbin Engineering University,Harbin 150001,China)
Load identification in time domain is applicable to both linear systems and nonlinear systems in comparison with that in frequency domain.Besides,the time domain method can deal with transient impact force problem effectively.In recent years,more attention has been paid to the time domain method.In this article,some popular time-domain methods, such as inverse convolution method,weighted acceleration technique,function approximation technique,Kalman filter and recursive least square method,inverse system method and burgeoning intelligent algorithms,are summarized.In addition, the merits and demerits of these approaches are analyzed in the aspects of research objects,identification method and application area.It is indicated that nonlinear system and linear time-variant system will become the research focus,the inverse system method combined with modern intelligent algorithm will become a new research hotspot,and application of load identification to fault diagnose will be a development trend in the future.
vibration and wave;load identification;inverse problem;time domain identification methods;review
TB53;TU312;O327
A
10.3969/j.issn.1006-1335.2014.01.002
1006-1355(2014)01-0006-06
2013-04-01
国家自然科学基金资助项目(基金编号:50979016);中央高校基本科研业务费专项资金项目(基金编号:HEUCFZ1115)。
周盼(1986-),女,河北省深州市人,博士,目前从事载荷识别、振动和噪声控制研究。
E-mail:zhoupan734@163.com
李玩幽(1972-),男,教授,博士生导师,主要从事轴系振动、振动与噪声控制、故障诊断方面的研究。
E-mail:hrbeu_ripet_lwy@163.com
