基于共振梁后节点小幅振动的能量转化

何 伟，刘 鹏，刘昌海

(1.三一重工股份有限公司，长沙 410100;2.同济大学 机械与能源工程学院，上海 201804)

共振破碎机工作时，共振梁作受迫振动，在输入端输入简谐激励，使得安装于共振梁输出端的锤头产生振动，敲击地面并引起水泥混凝土地面的破碎.锤头与地面的碰撞使得共振梁受到较大的反作用冲击力，在此力的影响下，共振梁的振动形态发生不规则变化，如振动幅度增大甚至共振梁“弹起”等，不利于水泥路面的破碎.为了稳定共振梁的振动，破碎机采取了一些减振措施来消除或减小碰撞对振动系统的影响，但对其减振的实质和能量转化过程却研究较少.

1 减振技术

针对碰撞冲击问题，现在主要的减振方法是利用与液压缸安装配合的减振重物及阻尼元件［1］来实现减振.具体做法是:将液压缸的一端悬挂于共振破碎机机架立柱上，另一端与减振重物连接，减振重物和共振梁之间装配有阻尼元件(如橡胶减振片等).当共振破碎机工作时，液压缸泄压，减振重物依靠自身重力紧压在共振梁后节点处，使得破碎锤头与地面紧密接触;当共振梁受到路面的反冲击作用时，重物紧压在共振梁上避免其弹起，同时阻尼元件可吸收冲击能量，如此即可避免共振梁的振动形态发生过大变化.共振破碎机减振系统结构如图1所示.

2 共振梁后节点的小幅振动设想

对于上述减振方式，多数文献资料中只是进行了大致的描述，没有具体分析减振中系统的能量转化过程，这主要是因为共振梁是一种柔性体结构，其振型描述较为复杂.徐海［2］在其论文中利用ADAMS软件对振动系统进行仿真，研究配重质量的变化对机架重心加速度的影响，但也没有选择合适的理论对能量转化过程进行深入分析.

图1 减振系统实体图Fig.1 Dam ping system

本文为解决这一问题，提出了在实际工作中共振梁后节点进行小幅振动的设想，并基于此设想较为圆满地解释了碰撞过程中系统的能量转化.设想主要内容有:仅在输入端简谐激励的作用下，共振梁振动时前后节点可保持固定不动的状态;在锤头与路面发生碰撞的过程中，碰撞产生的冲击能输入振动系统，共振梁的振动形态发生改变，使得共振梁后节点和安装于后节点处的重物发生小幅振动，通过减振重物和共振梁后节点的运动，碰撞冲击能转化为重物机械能和阻尼元件的损耗能.

3 振动系统能量转化

碰撞过程中系统的能量转化不易直接研究，本文将先考虑共振梁仅在简谐激励下的振动方程和能量转化.在此基础上，对系统施加碰撞力并通过减振重物及阻尼元件减振后，分析振动系统的能量转化方程.

3.1 简谐激励下系统能量转化

首先仅考虑共振梁在简谐激励下的振动.简谐激励的频率与共振梁固有频率相同，共振梁作受迫振动并达到共振，其振型为相对于两个固定节点的上下振动，如图2所示.图中x表示共振梁各点的坐标，yA表示共振梁各点振动的幅值.

图2 共振梁振型示意图Fig.2 Diagram of resonant beam mode

振型函数为

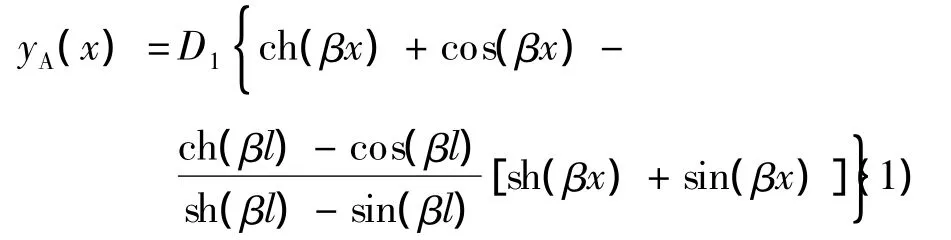
其固有频率为

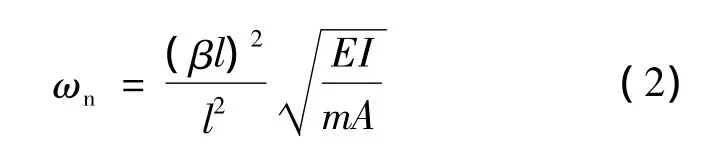
式(1)所示振型方程表示共振梁的振动形状，其中yA(x)表示共振梁x处节点的振幅，D1表示与振幅有关的比例，其数值大小由输入的简谐激励决定，l为共振梁的总长，β为特征值.式(2)中，ωn表示共振梁的固有频率，m表示梁的单位体积质量，A为梁的截面积，EI为截面抗弯刚度.

当系统稳定后，激振器输入的能量完全转化为共振梁自身的结构阻尼损耗.输入的简谐激励f随时间t的变化规律可表示为f=fmaxsin(ωt+φ)，其中fmax表示激励的最大值，ω表示输入激励的频率，φ表示初始相位，t表示时间.令式(1)中x=0，可得共振梁输入端的振动方程y(t)=yA(0)·sin(ωt)，其在一个周期T内输入的能量

根据工程断裂与损伤［3］，结构阻尼在一个很大频率范围内与频率无关，其消耗的能量与振幅的平方成正比，即

式中:η1为系数.故在一个周期内，振动系统能量转化方程可表示为

3.2 碰撞过程中系统能量转化

第3.1节得出了共振梁仅在简谐激励下的振型函数和能量方程，碰撞过程中若要达到需要的破碎效果，应使得振型函数与图2近似一致，此时共振梁的结构阻尼损耗可认为不变.

相对于在简谐激励下的振动，碰撞过程中系统的振动和能量转化过程显得更加复杂.碰撞时共振梁不仅受到简谐激励，还受到地面的反冲击力.系统损耗的能量也由多个部分组成:除共振梁结构阻尼损耗外，还包括水泥板块的应变能和阻尼元件的损耗能.其中，水泥板块的应变能是破碎路面的能量，阻尼元件的损耗能由共振梁后节点的小幅振动引起.碰撞过程中的能量转化可用图3所示流程图表示，图中虚线框表示共振梁仅在简谐激励下的能量转化过程.

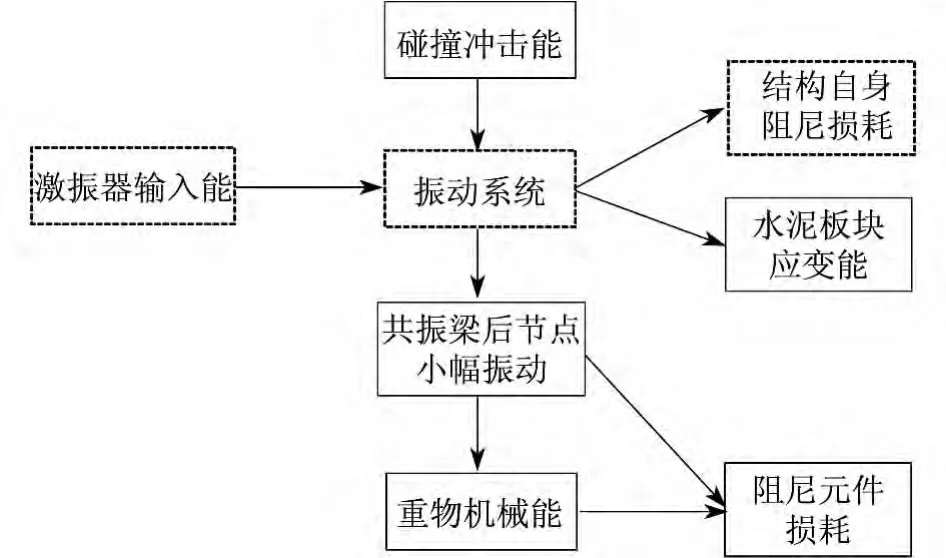
图3 碰撞过程能量转化流程图Fig.3 Energy transformation of resonant beam during collision process

如图3所示，振动系统的输入能量由两部分组成:激振器输入能，在第3.1节中已进行讨论;碰撞冲击能，此部分能量较难用数学表达式进行描述，但当系统稳定后，在一个周期内，此部分能量可视为定值Eim.

根据文献［3］，水泥板块的应变能

式中:Fq为广义力，根据赫兹接触模型，Fq=Kδe，其中K为赫兹刚度系数，e为刚性指数，反映了材料的非线性程度，一般取值为e≥1;δ为广义位移，此处δ=yA(l)，表示共振梁输出端振幅，由式(1)令x=l得到，故有

在减振重物和阻尼元件的作用下，当共振梁输出端受到路面的反冲击力时，共振梁仅有向上弹起的趋势，但不能发生不规则的杂乱振动.根据所作设想，共振梁后节点处进行小幅振动，使得与其配合安装的减振重物同时发生振动，碰撞冲击能转化为重物机械能和阻尼元件损耗能，并最终被阻尼元件消耗吸收，重物和阻尼元件的减振作用可用图4表示.

系统稳定后由于共振梁后节点的振动，碰撞产生的冲击能转化为重物的机械能和阻尼元件的损耗能，此过程能量转化方程可表示为

式中:Eim为定值;m1为减振重物的质量;ys为重物的振幅;C表示阻尼元件的阻尼系数;s表示阻尼元件的变形量，与重物和共振梁后节点的振动有关;g为重力加速度.

图4 系统减振流程图Fig.4 Flowchart of damping system

通过式(8)可以看出，由共振梁后节点振动引起的重物振动幅度与其自身质量m1有关，而阻尼系数C表征了系统吸收振动冲击的能力，适当增大减振重物的质量可减小共振梁后节点和重物自身的振动幅度.

碰撞过程完整的能量转化方程可表示为

方程左边表示激振器输入能量和碰撞产生的冲击能量，其中f'max表示碰撞过程中输入激励的最大值，f'max＞fmax，表现为此时的激振器输入能量大于式(3)中输入能量，其差值为破碎路面所需要的应变能.方程右边依次表示共振梁的结构阻尼损耗、水泥板块的应变能、重物机械能和阻尼元件的损耗能.锤头与路面碰撞后，由于减振重物和阻尼元件的作用，共振梁的振动形态变化较小，故认为振型函数(1)同样适合碰撞过程.

实际工作中，由于重物的质量很大，所以节点运动的最大位移很小，如此即可保证共振梁仍近似处于共振状态.系统稳定后，共振梁受到的反冲击能量被重物与共振梁连接处的阻尼元件所吸收.共振梁振动时，会引起构件之间(如吊耳与共振梁、吊耳与承载体之间等)的相对微小滑动，使得少部分能量转化为摩擦能而消耗，并且此部分能量较少，为方便分析，可以忽略.

4 ADAMS振动仿真

利用ADAMS软件可以进行系统振动的仿真，本文即用ADAMS软件验证所提出的共振梁后节点小幅振动设想的正确性.首先利用SolidWorks软件建立振动系统的仿真模型并导入ADAMS中，利用ANSYS软件将共振梁离散成柔性体后，导出为MNF文件，将ADAMS中的刚性体共振梁用此MNF文件替换［4］，并将其输入节点固定.

为达到高质量的仿真效果，本文对振动系统进行了详细的材料参数设置:共振梁三维尺寸为3.0，0.3，0.1 m;密度为 7 850 kg·m－3;泊松比为 0.3;弹性模量为200 GPa;共振梁固有频率为54 Hz;锤头设置为steel材料，其质量等信息由系统自动确定;重物质量设置为3 500 kg;水泥混凝土密度为2 400 kg·m－3，泊松比为 0.15，弹性模量为 30 GPa;在输入端添加简谐激励f=80 000sin(340t)，利用ADAMS的IMPACT函数在锤头与地面之间施加接触碰撞力，此碰撞力由弹簧阻尼模型［5］得出.建好的振动系统如图5所示.

图5 振动系统模型图Fig.5 Vibration system model

定义共振梁输出端MARKER_5为测试点，设置仿真时间为2 s，仿真步数为400，测得共振梁输出端的振动曲线如图6所示.

由图6可知，当系统稳定后，锤头的振动幅度并不是固定值，而是在一定的范围内变化，其平均振幅约为18 mm.其振幅的变化是因为共振梁的振动是无穷多阶振型的合成，并且振型合成中存在着耦合现象，故锤头的振幅难以维持在一个恒定值，而在一个范围内变化，此种情况仍能满足路面的破碎要求，故可认为本文所建的ADAMS仿真模型是合理的.

定义共振梁后节点处为MARKER_3，可测得其在碰撞过程中的振动曲线，如图7所示.

图6 共振梁输出端振动曲线Fig.6 Vibration wave of the output end of resonant beam

图7 共振梁后节点处振动曲线Fig.7 Vibration wave of the rear-node of resonant beam

根据图7所示振动曲线，在碰撞过程中当系统稳定后，共振梁后节点并不是固定的，而是进行小幅度振动，其平均振幅约为0.4 mm.如此可见本文对共振梁后节点进行小幅振动的设想是正确的，如此便可用此理论来进行共振系统的能量转化分析.仿真结果表明，重物的质量对共振梁后节点振动幅度影响较大，因篇幅有限，此处仅给出四组不同质量重物对共振梁后节点振动的影响，如表1所示.

表1 重物质量对共振梁后节点振幅的影响Tab.1 The effect ofmass on rear-node vibration amplitude

由表1可知，当重物质量较小时，对共振梁后节点的压力不够，此时共振梁振动形态发生改变，共振梁后节点振幅较大，共振梁输出端振幅偏小;随着重物质量的增大，共振梁后节点振幅减小，输出端振幅增大，这与前述章节的理论分析是一致的.根据仿真结果，重物质量选为3 500～4 500 kg是可取的.

5 结论

共振破碎机工作时，需要通过减振重物和阻尼元件对其振动系统进行减振，为分析此减振方式的实质及减振中的能量转化过程，本文提出了一种新的设想——共振梁后节点的小幅振动，并根据此设想较为理想地解决了碰撞过程中的能量转化问题.最后用ADAMS软件建立了振动系统的三维模型并进行了仿真，仿真结果表明，振动过程中在碰撞力、减振重物和阻尼元件的共同作用下，共振梁后节点作小幅振动.因此，本文提出的设想是正确的，并可采用此理论进行振动系统的能量转化分析.

［1］GURRIES R A，NEV R.Resonantly driven vertical impact system:US，157138［P］.1980 －06 －05.

［2］徐海.共振破碎机振动系统的动力学仿真研究［D］.武汉:武汉理工大学，2012.

XU Hai.Dynamics simulation research on vibration system of the resonant breaker［D］.Wuhan:Wuhan University of Technology，2012.

［3］庄茁，蒋持平.工程断裂与损伤［M］.北京:机械工业出版社，2004.

ZHUANG Zhuo，JIANG Chiping.Engineering breakage and damage［M］.Beijing:Mechanical Engineering Press，2004.

［4］李增刚.ADAMS入门详解与实例［M］.北京:国防工业出版社，2006.

LIZenggang.ADAMS introduction and examples［M］.Beijing:National Defense Industry Press，2006.

［5］LANKARANIH M，NIKRAVESH P.Continuous contact force models for impact analysis in multibody systems［J］.Nonlinear Dynamics，1994，5:193 －207.