双循环半群上的同余关系

关艺, 任苗苗, 陈益智

(1.西北大学数学学院,陕西 西安 710127;2.广东惠州学院数学系,广东 惠州 516007)

双循环半群上的同余关系

关艺1, 任苗苗1, 陈益智2

(1.西北大学数学学院,陕西 西安 710127;2.广东惠州学院数学系,广东 惠州 516007)

从双循环半群的同余关系出发,讨论了幂等元所在的同余类,证明了双循环半群上的一类同余ρd(d∈N)与其逆子半群之间的相互唯一确定关系,并对这种同余做成的集合进行了刻画,证明了这种同余做成的格与自然数集在某种偏序下做成的格同构,得到了一些有意义的结果.

双循环半群;同余;逆子半群;子格

1 引言及预备知识

设(S,·)是半群,若对任意的a∈S,S中有且仅有a的一个逆元,记为a−1,则称S为逆半群[1].设µ是逆半群S上最大的幂等元分离同余,若µ=1s,则称S为基本逆半群[1].用N表示所有自然数集,N×N为N与N的笛卡尔积集,其上的乘法为:由文献 [1]知,N×N 关于定义的乘法做成半群,且称此半群为双循环半群.设 S是逆半群,若S上的格林D关系为泛关系,即D=S×S,则称S为双单逆半群.若逆半群S既是基本的又是双单的,则称 S为基本双单逆半群.设 S是基本双单逆半群,Cω是 S的幂等元集,则在同构意义下,S就是双循环半群.设S是逆半群,若S上的格林J关系为泛关系,即J=S×S,则称S为单逆半群.设S是基本单逆半群,Cω是S的幂等元集,则在同构意义下,S就是双循环半群的逆子半群Bd(d∈N)[1].设L是一个格,X/=∅是L的一个子集,且对a,b∈X,均有a∧b∈X及a∨b∈X,则称X是L的一个子格[2].双循环半群作为一类特殊的逆半群,并且逆半群是正则半群,文献[3]给出了正则半群幂等元同余类的刻画,文献[4]对双循环半群上的同余结构进行了讨论,并给出了最小群同余的刻画,文献[5]研究了自反逆半群上的一类同余,文献[6]对于逆半群知识进行了系统阐述.本文在以上文献的基础上,对双循环半群〈N×N,·〉上的一类同余ρd(d∈N)进行探讨,得到了〈N×N,·〉上的同余ρd(d∈N)与其逆子半群Bd(d∈N)之间的相互唯一确定关系,进而给出这类同余的刻画.

2 主要结论

设〈N×N,·〉是双循环半群,d∈N.定义〈N×N,·〉上的二元关系ρd如下:

这样就有以下结果:

引理 2.1ρd是同余关系.

证明首先证明ρd是等价关系.

对任意的(m,n)∈N×N,因为d|0.所以d|(m−n)−(m−n),即(m,n)ρd(m,n),从而反身性成立.

对任意的(m,n),(m∗,n∗)∈N×N,若(m,n)ρd(m∗,n∗),则d|(m∗−n∗)−(m−n),进而有d|(m−n)−(m∗−n∗),即(m∗,n∗)ρd(m,n),从而对称性成立.

对任意的(m,n),(m′,n′),(m∗,n∗)∈N×N,若(m,n)ρd(m′,n′),(m′,n′)ρd(m∗,n∗),则有

d|(m′−n′)−(m−n),d|(m∗−n∗)−(m′−n′),

进而

d|[(m∗−n∗)−(m′−n′)]+[(m′−n′)−(m−n)],

于是d|(m∗−n∗)−(m−n),即(m,n)ρd(m∗,n∗),从而传递性成立.

下证 ρd满足左右相容性.若设 (m,n)ρd(m∗,n∗),则有 d|(m∗−n∗)−(m−n),对任意的(m′,n′)∈N×N,得

(m′,n′)(m,n)=(m′−n′+t,n−m+t),其中t=max(n′,m),

(m′,n′)(m∗,n∗)=(m′−n′+r,n∗−m∗+r),其中r=max(n′,m∗),

又因为

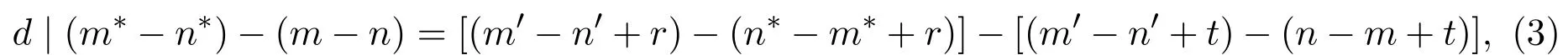
所以

(m′−n′+t,n−m+t)ρd(m′−n′+r,n∗−m∗+r),

即

(m′,n′)(m,n)ρd(m′,n′)(m∗,n∗),

因此ρd满足左相容.同理可证,ρd满足右相容.

综上,ρd是同余关系.

下面给出〈N×N,·〉上幂等元的刻画.

引理2.2(m,n)是〈N×N,·〉的幂等元当且仅当m=n.

证明(=⇒)设(m,n)是〈N×N,·〉的幂等元,则

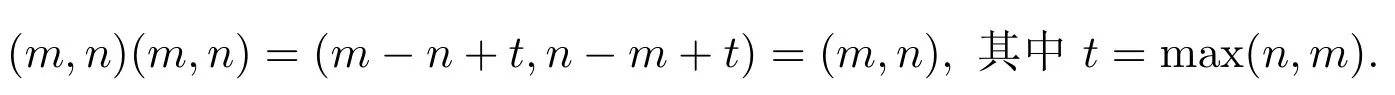
因为m−n+t=m,n−m+t=n,所以t=m=n.

(⇐=)(m,n)(m,n)=(m−n+t,n−m+t)=(m,n),其中t=max(n,m),因为m=n,所以t=m=n,于是(m,n)(m,n)=(m,n),即有(m,n)是幂等元.

由引理2.1、引理2.2得到了双循环半群〈N×N,·〉上的一类特殊的同余ρd(d∈N)以及〈N×N,·〉上幂等元的刻画.首先考虑幂等元所在的ρd类.

对任意的m∈N,由引理2.2知,(m,m)是〈N×N,·〉的任意幂等元,对(m,m)所在的 ρd类定义如下:

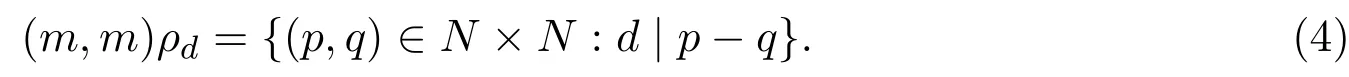
又对任意的n∈N,因为d|(p−q)−(m−m)=d|(p−q)−(n−n),所以

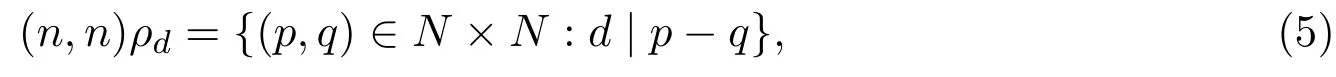
即得(m,m)ρd=(n,n)ρd.由此可知,任意两个幂等元都满足ρd关系,则所有的幂等元都在同一个ρd类中,因此同余ρd是幂等纯同余.

进一步有:

性质 2.1双循环半群〈N×N,·〉的幂等元所在的ρd类是基本单逆Cω半群.

证明对任意的(m,m)∈N×N,(m,m)ρd={(p,q)∈N×N:d|p−q},记

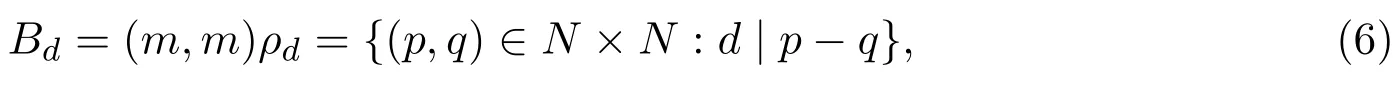
易证Bd是〈N×N,·〉的逆子半群,由文献[1]性质7.7知,Bd就是基本单逆Cω半群.

双循环半群 〈N×N,·〉的逆子半群 Bd(d∈N)的全体做成的集合记为 B,双循环半群〈N×N,·〉上的一类同余ρd(d∈N)的全体做成的集合记为C.

以下讨论集合 B与集合 C之间的关系.任意给定一个数 d(d∈N),都可由 d构造双循环半群 〈N×N,·〉上的同余 ρd,又因为幂等元所在的 ρd类就是 Bd,即任给一个 ρd都有唯一的 Bd与之对应.同样的,任给一个基本单逆 Cω半群,由文献 [1]性质 7.7知,都有唯一的 Bd(d∈N)与之对应,进而数d(d∈N)也随之确定,通过数d(d∈N)又可确定一个同余 ρd.由此可见 〈N×N,·〉的逆子半群 Bd(d∈N)与其上的一类同余ρd(d∈N)之间可相互唯一确定.设映射 ϕ:B→ C.对任意的 Bd∈B,使得 ρd=ϕ(Bd).对任意的ρd1,ρd2∈C,若ρd1=ρd2,则(m,m)ρd1=(m,m)ρd2,即有Bd1=Bd2,从而ϕ是单射.对任意的ρd∈C,可得(m,m)ρd=Bd,使得ρd=ϕ(Bd),从而ϕ是满射.因此可以给出如下结论.

结论 2.1集合B与集合C之间可建立一一对应.

3 关于集合C的刻画

双循环半群〈N×N,·〉上同余的全体在包含关系下做成的格记为L=〈con(N×N,·),⊆〉.

定理3.1集合C是格L的子格.

证明由C={ρd|d∈N},需证明对任意的ρd1,ρd2∈C,有

其中[d1,d2]、(d1,d2)分别是d1、d2的最小公倍数和最大公约数.

首先,证明C在“∧”运算下封闭.

易证ρd1∧ρd2=ρd1∩ρd2.因为ρd1∩ρd2⊆ρd1,ρd1∩ρd2⊆ρd2,所以ρd1∩ρd2是ρd1,ρd2的下界.设ρd是ρd1,ρd2的任一下界,则ρd⊆ρd1,ρd⊆ρd2,进而ρd⊆ρd1∩ρd2.

所以ρd1∩ρd2是ρd1,ρd2的最大下界,即ρd1∧ρd2=ρd1∩ρd2.

现证ρd1∩ρd2=ρ[d1,d2].

(⇒)对任意的((m,n),(p,q))∈ρd1∩ρd2,则((m,n),(p,q))∈ρd1,((m,n),(p,q))∈ρd2,即有

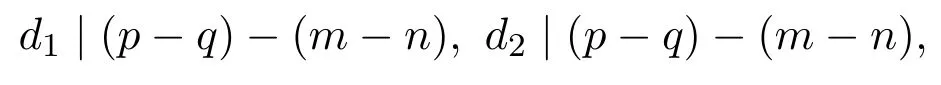
进而[d1,d2]|(p−q)−(m−n),所以((m,n),(p,q))∈ρ[d1,d2],由此可得ρd1∩ρd2⊆ρ[d1,d2].

(⇐)对任意的((m,n),(p,q))∈ρ[d1,d2],则[d1,d2]|(p−q)−(m−n),即有

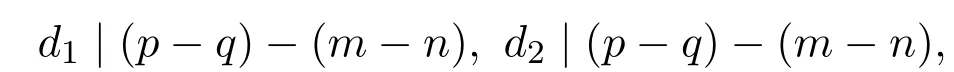
进而((m,n),(p,q))∈ρd1,((m,n),(p,q))∈ρd2,所以((m,n),(p,q))∈ρd1∩ρd2,由此可得ρ[d1,d2]⊆ρd1∩ρd2.综上,ρd1∩ρd2=ρ[d1,d2].

其次,证明C在“∨”运算下封闭.

对任意的((m,n),(p,q))∈ρd1,则d1|(p−q)−(m−n),进而(d1,d2)|(p−q)−(m−n),所以((m,n),(p,q))∈ρ(d1,d2),由此可得ρd1⊆ρ(d1,d2).

对任意的((m,n),(p,q))∈ρd2,则d2|(p−q)−(m−n),进而(d1,d2)|(p−q)−(m−n),所以((m,n),(p,q))∈ρ(d1,d2),由此可得ρd2⊆ρ(d1,d2).

综上ρ(d1,d2)是ρd1,ρd2的上界.

设ρd是ρd1,ρd2的任一上界,则ρd1⊆ρd.对任意的((m,n),(p,q))∈ρd1,有

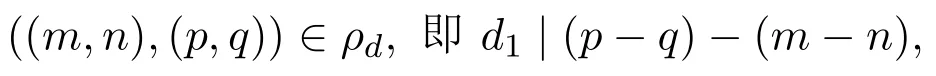
可推得d|(p−q)−(m−n).又有ρd2⊆ρd,则对任意的((m,n),(p,q))∈ρd2,有

可推得d|(p−q)−(m−n),因此,d|(d1,d2).

以下证明 ρ(d1,d2)⊆ρd.

任给((m,n),(p,q))∈ρ(d1,d2),有(d1,d2)|(p−q)−(m−n),进而

d|(p−q)−(m−n),即((m,n),(p,q))∈ρd,

因此 ρ(d1,d2)⊆ ρd. 由此可得 ρ(d1,d2)是 ρd1,ρd2上界中最小的,即 ρd1∨ρd2= ρ(d1,d2). 因

为d1,d2∈N,所以[d1,d2],(d1,d2)∈N,则

ρd1∧ρd2=ρ[d1,d2]∈C,ρd1∨ρd2=ρ(d1,d2)∈C.

综上可知,集合C是格L的子格.

设N是自然数集.定义N上的二元关系“≤”如下:

这样就有:

引理 3.1〈N,≤〉是格.

证明首先证明“≤”是偏序关系.对任意的a∈N,因为a|a,所以a≤a,从而自反性成立.对任意的a,b∈N,若a≤b,b≤a,则b|a,a|b,因此a=b,从而反对称性成立.对任意的a,b,c∈N,若a≤b,b≤c,则b|a,c|b,于是c|a,即a≤c,从而传递性成立.

下证〈N,≤〉中任意两元的最大下界和最小上界都存在.需证对任意的a,b∈N,有

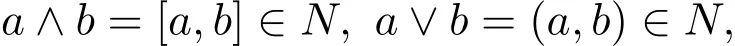
其中[a,b]、(a,b)分别是a,b的最小公倍数和最大公约数.

对任意的a,b∈N,因为a|[a,b],b|[a,b],所以[a,b]≤a,[a,b]≤b,即[a,b]是a,b的下界.设c是a,b的任一下界,则有c≤a,c≤b,于是a|c,b|c,进而[a,b]|c,因此c≤[a,b],从而[a,b]是a,b的最大下界,即a∧b=[a,b].类似可证,(a,b)是a,b的最小上界,即a∨b=(a,b).

综上,〈N,≤〉是格.

接下来考虑以上两种格之间的关系,得到如下定理:

定理3.2格C与格〈N,≤〉同构.

证明设映射ϕ:〈N,≤〉→C.对任意的a∈N,使得ρa=ϕ(a).显然ϕ是双射.下证ϕ是同态映射.

对任意的a,b∈N,因为

ϕ(a∨b)=ϕ((a,b))=ρ(a,b)=ρa∨ρb=ϕ(a)∨ϕ(b),

且有

ϕ(a∧b)=ϕ([a,b])=ρ[a,b]=ρa∧ρb=ϕ(a)∧ϕ(b),

所以ϕ是同态映射.

参考文献

[1] Howie J M.An introduction to Semigroup Theory[M].New York:Academic press,1976.

[2] 盛德成.抽象代数[M].北京:科学出版社,2001.

[3] 乔占科.正则半群的幂等元同余类[J].纯粹数学与应用数学,1995,11(1):69-71.

[4] 徐文锋.双循环半群上的同余结构[J].韶关学院学报:自然科学版,2012,33(8):11-13.

[5] 黄天霖.E-自反逆半群上的Cli ff ord同余[J].纯粹数学与应用数学,2005,21(3):255-262.

[6] Petrich M.Inverse Semigroups[M].New York:Wiley,1984.

Congruence relations on a bicyclic semigroup

Guan Yi1,Ren Miaomiao1,Chen Yizhi2
(1.Department of Mathematics,Northwest University,Xi′an 710127,China; 2.Department of Mathematics,Huizhou University,Huizhou 516007,China)

This paper is devoted to study congruences on a bicyclic semigroup.It is shown that there is an unique bijection between a class of congruences ρd(d∈N)on it and its inverse subsemigroups.Also,the lattice of such congruences and the lattice of natural numbers under some partial order are isomorphic.

bicyclic semigroup,congruence,inverse subsemigroup,sublattice

O152.7

A

1008-5513(2014)04-0435-06

10.3969/j.issn.1008-5513.2014.04.014

2014-04-30.

广东高校优秀青年创新人才培养计划项目(2013LYM0086).

关艺(1989-),硕士生,研究方向：代数学.

2010 MSC:20M18