基于混沌理论的滚动轴承故障信号判据

任学平，刘桐桐

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

旋转机械是应用广泛的机械设备，在各行各业中都起着至关重要的作用，而轴承则是旋转机械设备的主要部件，由轴承故障导致的旋转机械故障占到其总故障的一半以上，造成了巨大的经济损失[1]。

Duffing振子方程是近几年提出的能够判断机械故障的有效方法之一，该方法对特定频率的微弱正弦信号具有敏感依赖性，而对其他无关信号则具有很强的抑制作用[2-3]，能够检测出淹没在强噪声信号中的微弱正弦信号。可用于判断旋转设备故障。

1 Duffing振子基本理论

传统的Duffing振子方程为

x″+kx′-αx3+βx5=frcos(ω0t)+s，

(1)

式中：-αx3+βx5为非线性恢复力；frcos(ω0t)为内置周期策动力；k为阻尼系数；s为待测信号。

利用四阶Runge-Kutta法[4]对(1)式进行微分求解并令x′=y， 则(1) 式变形为

(2)

混沌系统的一个主要特征就是存在混沌吸引子，并且每一个参数变量都对应着一个奇怪吸引子，传统方程存在5个参数变量，因此得到的相轨迹应该是5条曲线的混合体。

方程中的限制参数越多，最终得到的结果就越接近真实情况。因此在上述方程的基础上，对Duffing方程进行改进，对方程的嵌入维数和最大lyapunov指数进行计算[5]，并经过多次尝试，最终将传统方程的非线性恢复力由-αx3+βx5变为-αx3+βx5+γx7，此时得到的混沌方程仍然具有混沌特性，限制参数则由原来的5个变为6个，更能够反映待测信号中故障信息的特征参数。变形之后的方程为

(3)

现令s=acos(15t)+randn(1,n)，将其加入(3)式中，利用MATLAB进行仿真，结果如图1所示，图中横、纵坐标分别表示输出信号的速度(m/s)、位移(m)(图4、图6同)。由图可知，加入模拟信号后，系统由混沌状态进入到大尺度周期状态，证明了微弱正弦信号的存在。

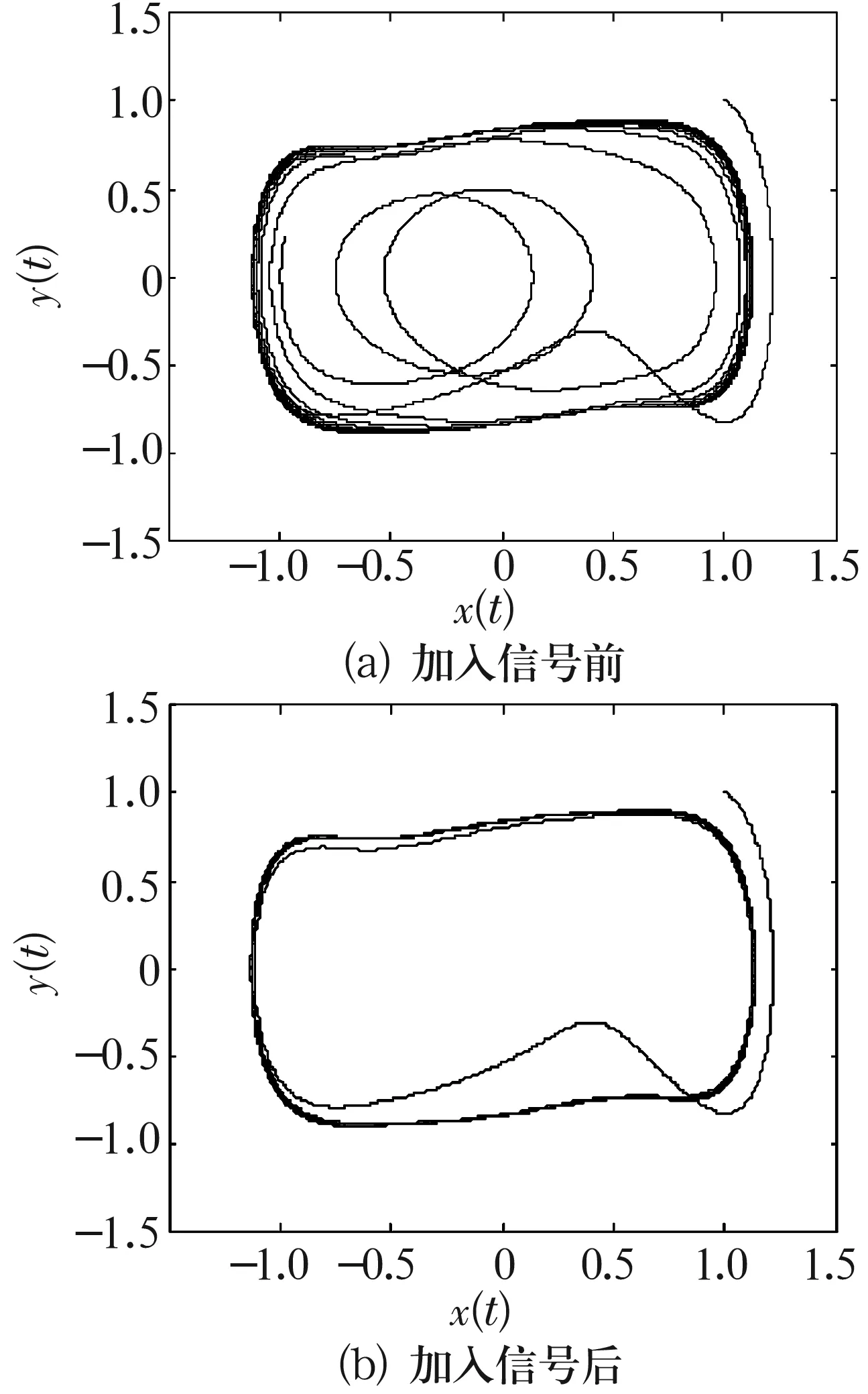
图1 加入模拟信号前后系统的相轨迹

研究发现，系统的输出和的方差具有一定的规律性：当外加周期信号的频率与内置周期策动力的频率相同时，系统的输出和的方差最大；而当两者频率不相同时，系统的输出和的方差总是偏小于该最大值；并且当外加周期信号的频率接近于内置周期策动力的频率时，系统的输出信号相比其他值会发生明显的变化。对上述模拟信号进行处理得到的输出信号x(t)和y(t)的方差如图2所示。

通过图2可以看出，当内置周期策动力频率fr=15 Hz时，2个方差均出现了很大的波峰，从而也反映出待测模拟信号中存在频率为15 Hz的微弱周期信号。与给定的输入模拟信号相吻合。利用改进的Duffing方程通过2种不同的角度都能判断出故障信号的存在，证明了该方法的有效性和可行性。

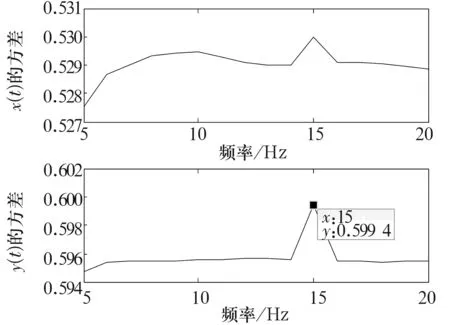
图2 模拟信号最大lyapunov指数图

2 利用改进方程检测旋转机械故障

通过模拟信号对改进方程进行的仿真，证明改进方程能够检测出故障信号，为进一步证明该方法在现场环境中也能检测出旋转机械的故障信号，分别利用Duffing方程对参数(节圆直径、滚动体直径、滚动体数、接触角)已知和未知的轴承进行检测。检测数据通过振动测试试验台获取，测量时采用3通道加速度传感器，采样频率为2 000 Hz，电动机转速为1 450 r/min。

2.1 已知参数的轴承信号检测

测试轴承为N205EM圆柱滚子轴承，轴承安装在振动测试试验台上，外圈固定，内圈旋转，测试装置如图3所示。

图3 轴承信号采集装置

试验过程中，首先采集10组正常轴承信号，然后将轴承换成事先加工好的故障轴承(内圈故障、外圈故障及滚动体故障)。内、外圈故障采用钼丝切割机在滚道上切割深度和宽度均为0.5 mm、长度为套圈宽度的长方形槽，滚动体故障为直径0.5 mm、深度0.2 mm的小圆坑。

滚动体直径7.5 mm，滚子组节圆直径39 mm，滚动体数12，接触角0。数据的采样频率为2 000 Hz，采样点N=2 048，电动机转速n=1 450 r/min。计算所得轴承各部件故障频率见表1。

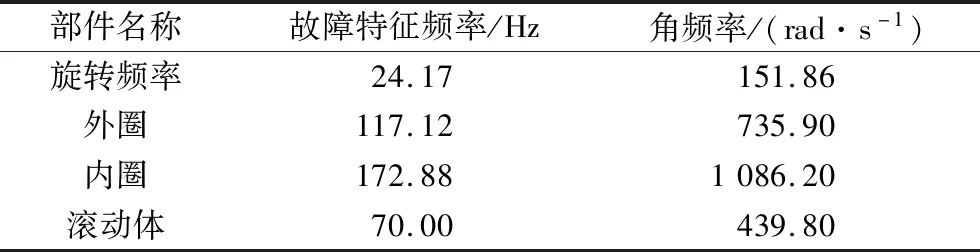
表1 轴承各位置故障频率

在此，针对外圈故障进行说明，其他故障与此同理。根据轴承外圈的各个特征参数设计出的Duffing振子方程为

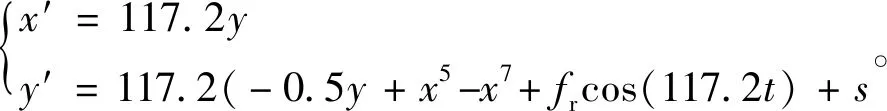
(4)

将采集到的3种故障信号加入到(4)式中，利用MATLAB进行计算，得到的相轨迹如图4所示。通过比较看出，系统只有在加入外圈故障时相轨迹变为周期状态，其余均处于混沌状态。说明该方法有效判断出了轴承故障位置。

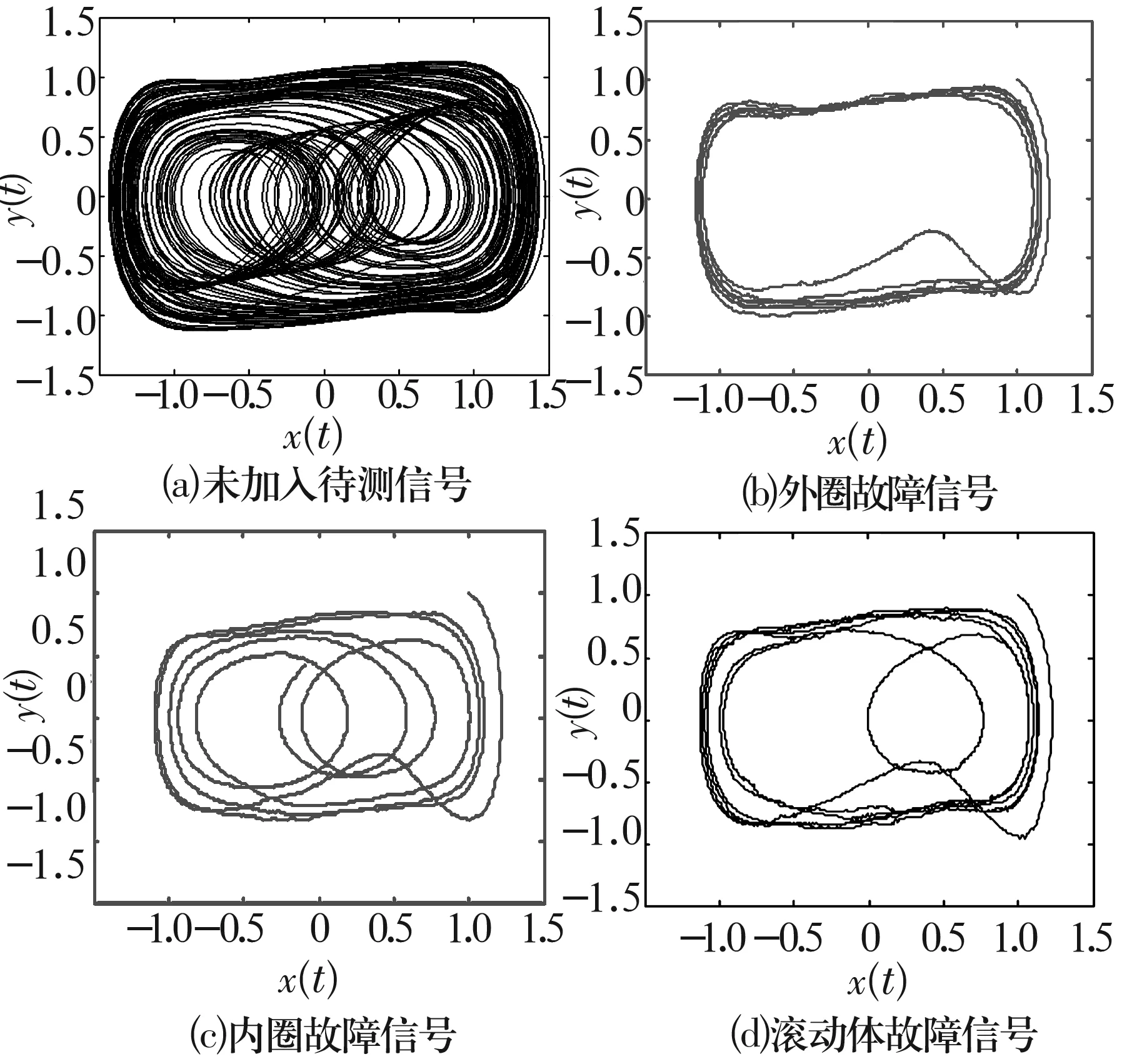
图4 加入待测轴承信号前后系统的相轨迹

2.2 未知参数轴承信号检测

在现场测试复杂设备的振动信号时，往往不知道其中部件的参数，当系统发生故障之后，对轴承内圈、外圈、滚动体各设计一个Duffing方程，分别去测试采集到的数据，系统相图发生变化的即为故障所处位置。

现以某内圈故障轴承为例进行分析，采集故障信号时将电动机转速设为1 200 r/min，用(3)式进一步计算，式中ω0在50～150 Hz之间变化，其余均为常数，ω0步长为1 Hz，计算得轴承故障信号在系统内置周期策动力发生变化时的输出方差如图5所示。

图5 轴承故障输出方差

通过图5可以看出，轴承故障在内置周期策动力频率为107 Hz时输出方差存在峰值，因此可以推断轴承的故障频率在107 Hz左右，据此设计的Duffing振子方程为

(5)

其中，ω在107 Hz附近变化，最终发现当ω=106.5 Hz时，将测得的轴承故障信号加入到(5)式中，系统相轨迹发生突变，得到的轴承故障相轨迹如图6所示。

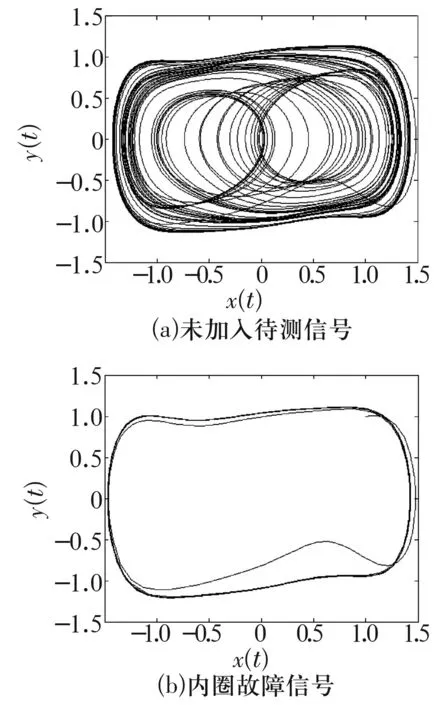
图6 内圈故障轴承的相轨迹

通过图6可以看出，在加入轴承故障信号之后，系统由混沌状态变为大尺度周期状态，反映出轴承故障信号中存在特征频率为106.5 Hz附近的微弱正弦信号。轴承的故障频率与其参数的关系为[6]

(6)

式中：Dw为滚动体直径，mm；Dpw为轴承节圆直径，mm；α为接触角；Z为滚动体数；n为轴承转速，r/min；fr为轴承转动频率。

同理，改变转速为1 450，1 500及1 750 r/min，将得到的特征频率分别代入(6)式，得到四元一次方程组，通过求解得Dw=8 mm，Dpw=39 mm，α=0°，Z=9，所得数据与6205-2RS SKF深沟球轴承数据相同，可以判断出故障轴承为深沟球轴承内圈故障，与事先给定的结果相同。

3 结束语

利用改进Duffing振子方程对参数已知和参数未知的滚动轴承故障进行判断得知，该方法能够判断出旋转机械部件的故障所在，并且简单直观，对于今后旋转机械故障信号的判别将会有很好的应用空间。