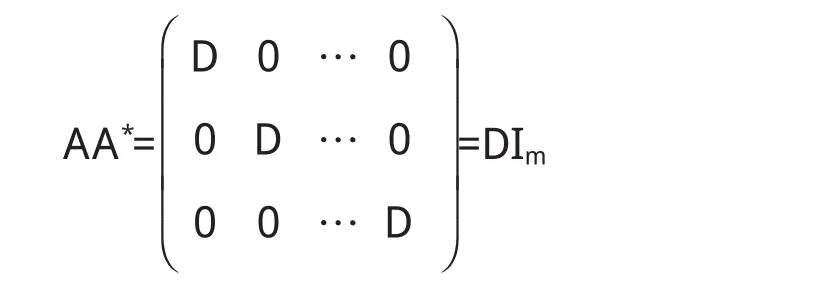谈行式与列式
2014-07-22贾美娥
贾美娥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
谈行式与列式
贾美娥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文主要讨论了行(列)式的展开与证明.
行列式;行式;列式
通常的行列式,其行数与列数必须相等,而行式与列式的行数与列数未必相等.
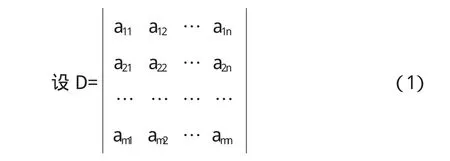
是一个m×n(m≤n)行式,则
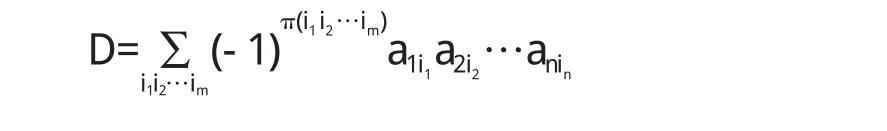
其中i1i2…im是1,2,…,m中n个数码的选排列. π(i1i2…im)是排列i1i2…im的反序数.
注:本文均用π(i1i2…im)表示排列i1i2…im的反序数.
设D是形如(1)的一个m×n(m≥n)的列式,则
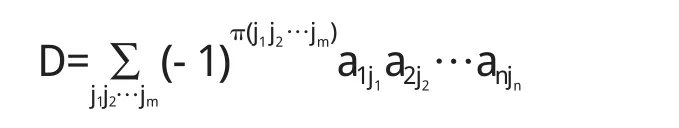
其中j1j2…jn是1,2,…,m,中nT数码的选排列.
不难证明,行式与行列式有相同的有关行的性质.列式与行列式有相同的有关列的性质,但对于行式的列和列式的行这些性质未必满足.在此这些性质就不一一列举.本文着重于行式、列式的展开式,只讨论行式,列式的有关性质同理可得.
定义1 设D是形如(1)的一个m×n行(列)式,D的元素aij的余子行(列)式,Nij指的是在D中划去元素aij所在的行及列后,剩下的元素构成的(m-1)×(n-1)行(列)式.Nij的元素ast(s=1,…,i-1,i+1… m;t=1,…,j-1,j+1,…,n)带上符号(-1)π(is)+π(jt)后构成的(m-1)×(n-1)行(列)式称为元素aij的代数余子行(列)式,记做Bij.
不难验证,当m=n时,Bij就是行列式D的元素aij的代数余子式.下面注明,行式与行列式一样也可以依行展开.首先证明如下定理1.
定理1若在形如(1)的m×n行式D的第i行的元素除aij外都是零,即MD等于aij与它的代数余子行式Bij的乘积:

证明 10首先假定D的第一行元素除aij外都是零,这时,

要证D=a1jB1j因

所以Bij的每一项都可写做:
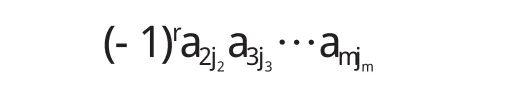
其中j2…jm是1,…j-1,j+1,…,n中m-1个数码的选排列,而且j2…jm恰有r个小于j.这一项在B1j中的符号为(-1)π(j2…jm),因此a1jB1j的每一项都可写做:a1ja2j2a3j3…amjm,其中jj2…jm是1,2…,n中mT数码的选排列.这一项在a1jB1j中的符号为(-1)r+π(j2…jm).由于j2,j3,…,jm,因此
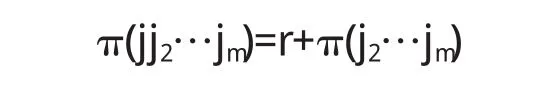
故(1)在a1jB1j中的符号为:(-1)n(jj2…jjn)
显然(1)也是D的项,而且D的每一项都可写成(1)的形式.(1)在D中的符号为

20证明一般情形,设

的第i行元素除aij外都是零,将D的第i行依次与i-1,…2,1交换,因交换行式的两行,行式改变符号,所以

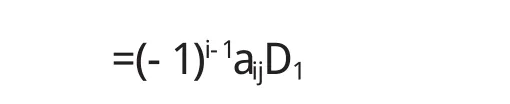
显然D1=(-1)i-1Bij,所以D=aijBij
定理2 m×n行式D等于它的任意一行的所有元素与它们的对应的代数余子行式的乘积的和.
换言之,行式有依行的展开式:
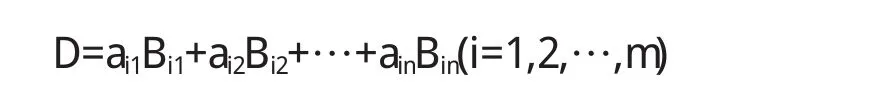
因行式对于行可拆项,所以定理的结论显然这里就不证了.下面的定理也是显然的.
定理3 行式的某一行元素与另一行对应元素的代数余子行式的乘积的和等于零.设D是形如(1)的一个m×n行列式,则有
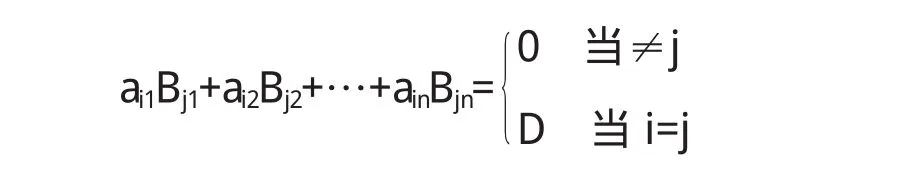
利用这一结果可求一些矩阵的广义逆.
设A=(aij)是一个m×n矩阵,称形如(1)中的D为矩阵A的行(列)式.称
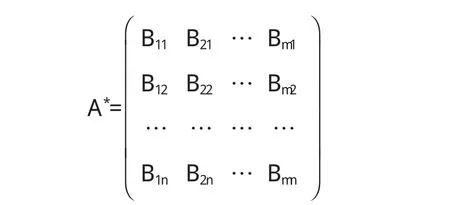
为矩阵A的广义伴随矩阵,其中Bij是D的元素aij的代数余子行(列)式,因为
〔1〕张禾瑞,郝炳新.高等代数第四版[M].高等教育出版社,1999.
O151.2
A
1673-260X(2014)04-0012-02