一个负系数的p叶解析函数的偏差定理
2014-07-22周海燕
周海燕
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
一个负系数的p叶解析函数的偏差定理
周海燕
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文引进一类负系数的p叶解析函数,用初等方法和从属关系讨论类中函数的系数不等式,由此推出该类中函数的偏差定理,推广文[2]中的相应结果.
p-叶;负系数;系数不等式;偏差定理
1 引言
设S(p)表示在单位圆盘U={z:|z|<1}内解析函数f(z)=zp+的全体组成的类,T(p)表示S(p)中具有形式

的函数全体.同样用s*(α,p),c(α,p)和Sn*(α,p)分别表示如下函数类:

C(α,p)={f∈T:∃g(z)∈s*(α,p),使得
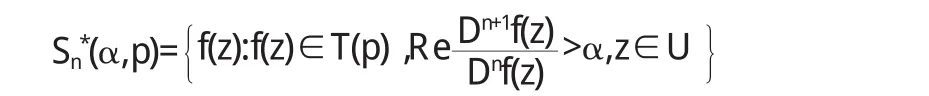
其中Dnf(z)为Salagean算子[1],且

显然S0*(α,0,0)=S*(α).
本文引进函数类:

则称f(z)属于函数类Cn(α,p).显然Cn(α,1)为文[2]中引进并讨论的函数类Cn(α).
本文用初等方法和从属关系讨论解析函数类Cn(α,p)的性质,得到讨论中函数的系数不等式,由此推出类中函数的偏差定理.推广[2]中的相应结果.
2 偏差定理
为了证明偏差定理,先给出类中函数的系数不等式:

证明若f(z)∈Cn(α,p),则有
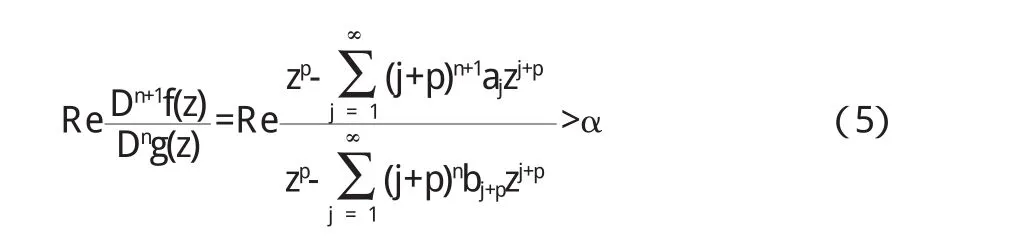
注意到z取实值时,((Dn+1f(z))/Dng(z))也为实值.令z→1¯则有

从而

反之,若(4)式成立,则有

当到Z取实值时,(Dn+1f(z)/Dng(z))也为实值.令z→1ˇ,则有
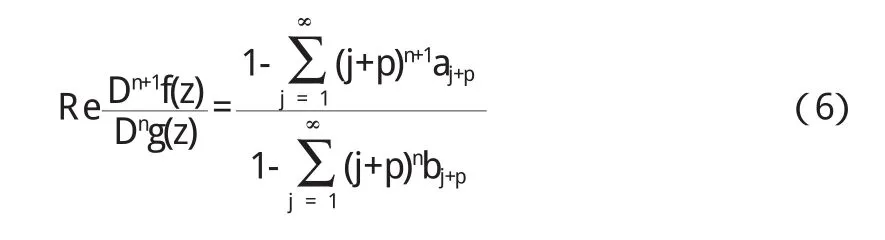
从(4)式得到

由此推出
∞
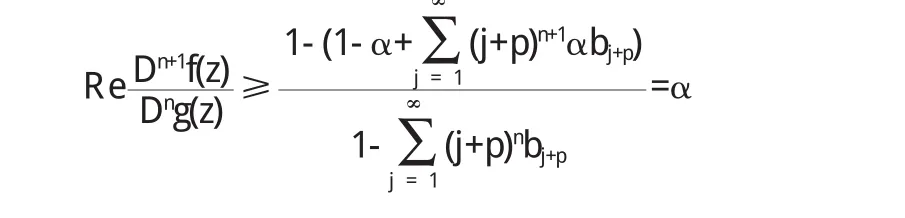
所以f(z)∈Cn(α,p).
当f(z)=g(z)时,从引理得到:
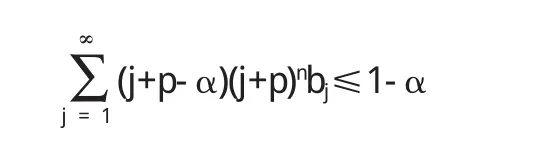
从推论1得到
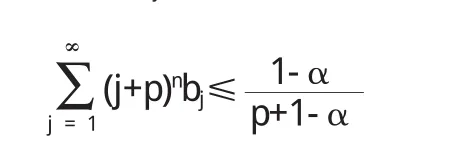
3 偏差定理
定理 由(1)式所确定的函数f(z)∈Cn(α,p),则有

是精确的,(7)和(8)式极值函数为
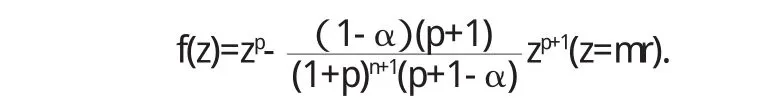
证明 设f(z)∈Cn(α,p),由引理可知
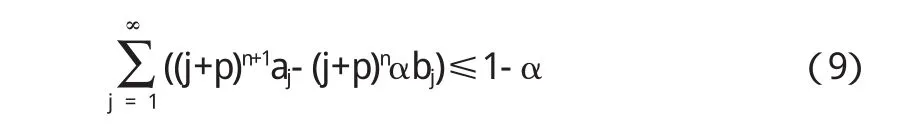
从(9)式推出
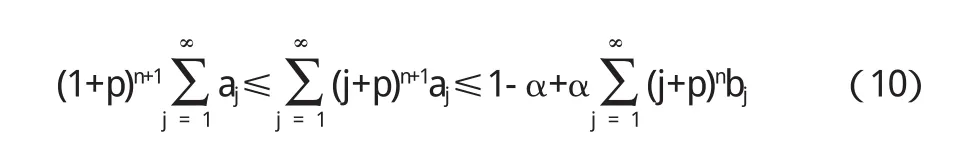
由推论2可知

则由(10)式和(11)式推出
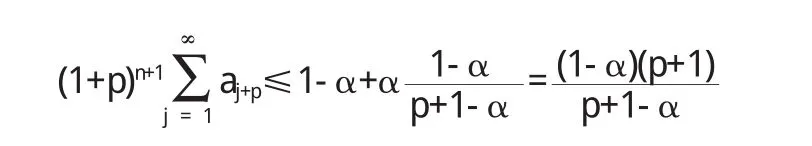
因此

由此推出(7)式成立.
又因为

利用(13)和(14)式,容易证明(8)式成立.
推论3在定理的假设下,函数f(z)包含在中心在原点,半径为r的圆内,这里

注:当引理和定理中取p=1时就得到文[2]中的相应结果.
〔1〕G S.Salagean Subclass of univalent functions[J].Lecture Notes in Math,pringer Berlin,S1983,pp.1013,362-372
〔2〕邓琴.负系数单叶函数的一个新子族[J].数学研究与评论, 2007,27(4):832-838.
〔3〕李书海.特殊解析函数[M].呼和浩特:内蒙古科技出版社, 2007.
O174.51
A
1673-260X(2014)04-0014-02
