基于核切片逆回归的轴承故障特征提取

周志才，刘东风，石新发

(海军工程大学 青岛油液检测分析中心，山东 青岛 266012 )

在工程实际中获得的机器信号往往含有噪声，且故障发生时机器不可能长时间运行，所得到的故障样本数量有限。为了更准确地识别机器的状态和故障，需通过多种物理量的特征信息进行判别，而利用高维小样本数据构造分类模型时容易产生过拟合现象。因此，故障特征信息的选取成为机械故障诊断的关键。

目前常采用主成分分析(Principal Component Analysis, PCA)对高维故障数据进行压缩，提取能较好反映故障信息的特征。PCA提取的只是原始特征中的线性成分，而在监测和诊断中反映机器状态的大量信息蕴含在数据的非线性成分中。文献[1-2]引入核函数概念，将低维不可分的非线性特征映射到高维可分空间，由此产生核主成分分析(Kernel Principal Component Analysis,KPCA)的概念。KPCA虽很好地考虑了非线性，但在提取新的分类特征向量时，未区别样本类内、类间信息，因此对于构建故障模式识别模型通常并非最优。

下文考虑采用一种能较好利用先验信息进行类间区分的非线性特征提取方法——核切片逆回归(Kernel Sliced Inverse Regression, KSIR)，阐述其基本思想和算法，同时采用KSIR和KPCA对轴承故障试验数据进行维数压缩和特征提取的对比分析，并讨论相关参数的选择对KSIR特征提取能力的影响。

1 KSIR的基本思想和算法

1.1 基本思想

切片逆回归(Sliced Inverse Regression, SIR)是由文献[3]提出的结合逆回归和PCA的算法，其在寻找最优投影方向时考虑输出变量(响应变量)和输入变量的信息，实现高维数据的综合降维。

假设x为由n个p维观察样本xi(i=1,…,n)组成的n×p维观察矩阵，y为n×1的输出变量，文献[3]提出

y=f(β1x,β2x,…,βKx,ε)，

(1)

式中：f为RK+1空间的未知函数；β1,β2,…，βK为K个未知向量；ε为与x独立的分布未知的随机误差。

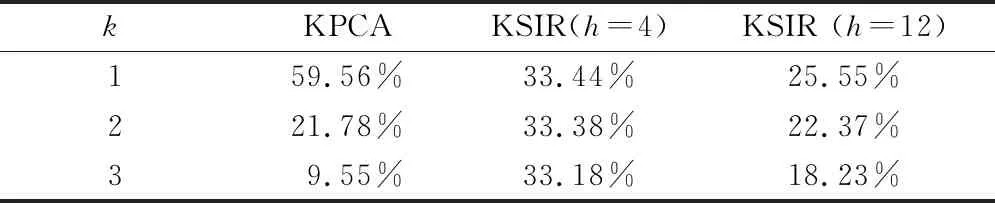
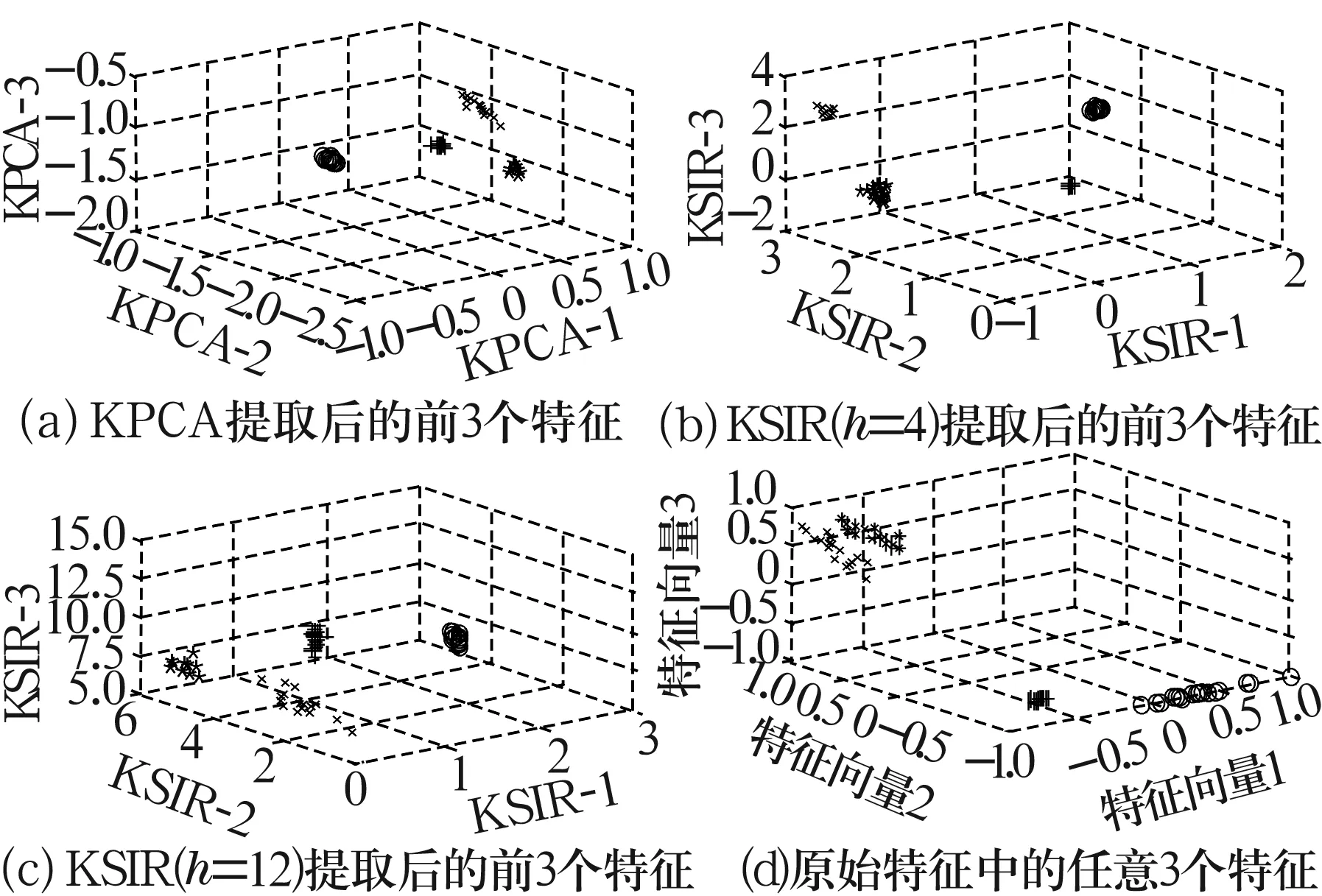
当此模型成立时，p维原始样本空间变量便映射到K维空间(β1x,β2x,…,βKx)T上，且保留关于y的所有信息。当K

为寻找EDR方向，用逆回归思想将x和y颠倒角色，由求解p维回归变成一维回归，直接避开高维带来的复杂问题。当y发生变化时，E(x|y)构成1条曲线，称为逆回归曲线。由此证明，对x进行标准化矩阵z的逆回归曲线E(z|y)包含在由标准化的EDR方向β1,β2,…，βK构成的线性空间中，协方差矩阵ΣηCov(E(z|y))在任何一个与βk(k=1,…,K)正交的方向上都退化，从而对应于Ση的最大K个特征值的标准化特征向量βk(k=1,…,K)就是标准化的EDR方向。

切片的思想便是根据y将样本“切”成h片，然后在每个切片内计算样本均值，并由此估计总体协方差矩阵，运用PCA求得E(x|y)的前K个EDR方向。

考虑到样本各物理量间的复杂非线性关系，引入Mercer核函数，通过由核函数定义的非线性映射Φ将初始样本空间变换到高维特征空间，高维空间映射向量的点积运算转换为原始样本空间数据向量的数学运算，避免直接构造映射函数的麻烦，同时也极大减小计算过程的复杂度和数据的存储量，由此便将线性SIR发展为非线性KSIR[4]。

1.2 算法

KSIR通过Φ将样本映射到更高维空间[5]中，即

Φ:xi→Φ(xi)。

(2)

此时， (1)式变为

y=f(β1Φ(x),β2Φ(x),…,βKΦ(x),ε)。

(3)

利用前述SIR思想对(3)式进行计算求得EDR方向，具体计算过程为：

(1)首先对Φ(x)进行零均值化处理，使满足E(Φ(x))=0，定义Φ=[Φ(x1),…,Φ(xn)]T，样本协方差矩阵为

(4)

(2)根据y将样本切成h片后进行分组，每组切片内的相应映射样本均值为

(5)

式中：ni为第i切片组内的样本数；Ii为第i切片组。

(3)利用每组切片的样本均值和容量加权值计算总体样本协方差矩阵为

(6)

(4)将Φ沿KSIR的前r个方向投影，即得前r个主要成分。

2 试验与结果分析

2.1 KSIR与KPCA在故障特征提取中的对比分析

试验采用美国Case Western Reserve University的SKF 6023深沟球轴承故障振动数据[6]。轴承故障数据试验平台示意图如图1所示，包括1台1.47 kW的电动机、1个转矩传感器、1个功率计和电子控制设备，试验轴承支承电动机轴。使用电火花加工技术在轴承上布置单点故障，深度为0.533 4 mm，设置正常轴承、内圈故障、外圈故障、球故障4种单一故障类型，将振动信号中每4 096个点作为1个样本，每类各20个样本。为了获取较全的故障特征信息，从样本中提取时域、频域和经验模态分解能量熵等共43维故障特征[7]，构成80×43维的故障样本矩阵。

图1 轴承故障数据试验平台示意图

表1 3种提取方法下特征向量对自变量的解释能力比较

对于KPCA，特征向量的解释能力逐渐下降，前3个特征向量的累计贡献率已达90.89%，在维数压缩的同时关键信息丢失较少；对于KSIR，特征向量对自变量的解释能力则相对较平均，h取4时，前3个特征向量的累计贡献率达100%，意味着故障关键信息仅通过映射后的3个特征向量便足以表达，大大减少后续训练模型的复杂程度和计算量；当h大于类别数(h=12)时，可明显看出特征提取能力不但未增加，反而比KPCA还差，这是由于KSIR对切片分组过于依赖。

方差贡献率ηk只是在每种方法所获得的EDR空间进行相对比较。为了比较3种方法下映射到前3个EDR方向的特征向量对故障信息的提取效果，将3种方法映射后的80×9维的特征向量矩阵作为原始特征向量，采用文献[7]提出的特征选择的改进方法对其进行计算，各特征向量分类性能比较如图2所示，值越大则表示特征向量的分类性能越好。

图2 各特征向量分类性能比较

由图2可知，在相同评判条件下，KSIR(h=4)映射后的特征向量的故障分类性能最佳，KPCA中方差贡献率最大的第1个特征向量仅保留原样本较多的关键信息，但从分类性能来讲，第3个特征向量却优于第1个特征向量。

由于类的可分性不仅取决于均值的可分性，还依赖于方差的可分性，所以特征向量对因变量的解释能力可在图3所示的前3个特征向量组成的三维空间中的分布得到解释。图3d为原始特征样本中随机选取的三维特征组成的分布图，其类别均值的可分性较差，直接采用此原始特征进行判别易产生较高误判率；图3a的KPCA和图3c的KSIR(h=12)方法，类别均值的可分性较明显，但各类别的方差较大，由此表现出的发散性易引起类别间的误判；图3b的KSIR(h=4)方法，不仅类别间边界明显，而且同类样本个体聚集紧密，类别信息对特征向量提取的贡献得到充分体现。

图3 样本在特征空间的分布

综上所述，KSIR借助核函数实现分类属性与类别信息间的内在非线性关系，在取得合适h时可用较少特征向量获得对自变量和因变量较强的解释能力，而且在低维的EDR空间实现对数据的解释和可视化，分类性能优于KPCA。

2.2KSIR中h与r的选择

由2.1节可知，在h选取不当时，原始特征信息在r维主分量上投影时产生较大的丢失。为了研究h与r对原始特征信息提取能力的影响，h与前3个特征向量累计贡献率的关系如图4所示。

图4 h与前3个特征向量累计贡献率的关系

由图4可知，随h增加，前3个特征向量累计贡献率呈逐步下降的趋势，切片是为了考虑样本的先验类别信息，因此当h大于样本类别数时，相同类别不同切片内的样本在投影后间距变大，从而可在更多的EDR方向上进行细分。图4也间接验证h与非零EDR空间维数K间的关系[8]：K=h-1。当h小于样本类别数时，前K维特征向量的累计贡献率虽为1，但由于把不同类别的故障样本放到同一切片组内考虑，导致故障类别间的差距信息丢失，造成分类能力降低，故在使用KSIR进行降维特征提取时，当h等于样本类别数时，为了使分类性能最优，r应当在2≤r≤K间根据需要进行选择。

3 结束语

KSIR能考虑数据间的非线性关系，通过非线性映射将原始故障样本映射到高维空间；然后对样本切片分组计算EDR方向，获得投影到EDR方向上的特征向量，实现对原始样本故障信息基本无损失的降维提取；最后采用试验分析了KSIR相比于KPCA的优越之处。结果表明，KSIR考虑样本类别的先验信息，能以更少、分类能力更优的特征向量取得更高的分类精度。另外，分析讨论了KSIR中相关参数的确定，为KSIR应用于实际的故障模式判别和分类提供参考。