基于有限元法的自润滑关节轴承静力学分析

2014-07-21胡宝根王卫英岳琳琳

轴承 2014年4期

胡宝根，王卫英，岳琳琳

(南京航空航天大学机电学院，南京 210016)

自润滑关节轴承由一层很薄的衬垫粘结在关节轴承外圈内表面，与轴承内圈外表面形成摩擦副进行工作。具有结构简单、体积小、耐冲击、耐腐蚀、吸振、适应温度范围广和寿命长等特点，此外还具有在工作过程中免维修和无需添加润滑剂等优异特性，广泛应用于航空航天、工程机械、水利设施及军工机械等方面[1-3]。

自润滑关节轴承内、外圈之间为球面接触，到目前为止，利用解析的方法求解其内、外圈及衬垫的应力分布和变形有一定困难。随着计算机数值模拟技术和有限元方法的不断发展，利用有限元法对关节轴承进行力学和摩擦学性能研究已逐渐取代传统的解析法分析[4-5]。目前，已有大量文献利用有限元分析软件对关节轴承进行力学和结构分析，但多侧重于关节轴承内、外圈的接触应力及其尺寸的相关优化，而对自润滑关节轴承衬垫结构的研究报道较少。研究衬垫的应力分布、接触应力变化和变形情况，不仅可以为自润滑衬垫材料的选择提供参考，还可为自润滑关节轴承的失效机理和优化设计提供理论依据。

1 结构和材料参数

向心关节轴承工作时主要承受径向载荷，以自润滑向心关节轴承GE30C为研究对象，对其进行静力学分析，研究径向载荷对轴承衬垫的影响。轴承由外圈、内圈和自润滑衬垫组成，其主要结构参数：内径d为30 mm,外径D为47 mm，内圈宽度B为22 mm，外圈宽度C为18 mm，球面直径dk为40.7 mm。聚四氟乙烯复合材料衬垫宽度为18 mm，厚度为0.5 mm，固定于轴承外圈内侧。轴承的额定动载荷为65 kN,额定静载荷为166 kN。滑动摩擦副为钢/聚四氟乙烯复合材料。分析时为了能有效模拟向心关节轴承静态试验条件，增加了加载板和心轴2个辅助零件。

由于聚四氟乙烯复合材料中聚四氟乙烯的含量一般较高，故这里直接采用纯聚四氟乙烯的参数进行模拟分析，自润滑关节轴承的材料相关参数见表1。

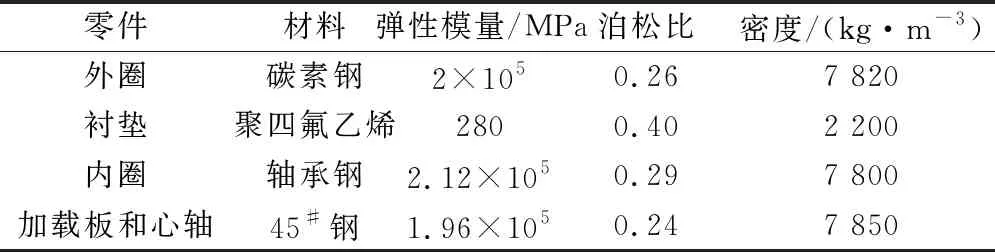
表1 自润滑向心关节轴承材料相关参数

2 有限元仿真模型的建立

将简化后的自润滑向心关节轴承模型导入ANSYS workbench中进行有限元分析，并添加材料信息并赋给相应的零件。文献[4]为了简化模型和减少计算时间，将心轴和加载板作为刚性体进行分析，这与实际工况不符，这里将心轴和加载板设为柔性体。

根据实际工况，在心轴表面，轴承内圈内、外表面，衬垫内、外表面，外圈内、外表面和加载板内表面均定义了接触类型。由于轴承的自润滑效应，将衬垫与内圈的接触类型设置为Frictional，输入摩擦因数为0.04。同时为了减少衬垫与内圈的渗透，将接触刚度stiffness设置为1，并采用Augmented Lagrange接触算法对该接触进行分析。除衬垫与外圈用黏合剂粘结在一起外，其他接触均为过盈配合。为加快分析的速度，均采用只需一次迭代的boned接触类型，并采用MPC作为接触算法。

根据模型的特征，受载后模型会发生变形，导致初始接触状态发生变化。为避免材料过度扭曲，对自润滑关节轴承内、外圈及衬垫采用6面体单元，网格划分方法为扫掠法(Swept Meshing)，并设置内、外圈网格大小为1 mm，衬垫层网格大小为0.5 mm。对心轴和加载板采用4面体划分网格法(Tetrahedrons)，设置单元大小为2 mm。关节轴承有限元模型如图1所示。

图1 自润滑关节轴承有限元模型

自润滑向心关节轴承能承受方向不变的载荷，在承受径向载荷Fr的同时能承受任一方向较小的轴向载荷Fa。当向心关节轴承承受恒定的径向和轴向载荷作用时，其当量动载荷的计算公式为

P=XrFr，

式中：系数Xr按表2选取。

表2 当量动载荷系数

由于该向心关节轴承工作时主要承受径向载荷，同时只承受较小的轴向载荷，Fa/Fr的比值趋于0，故作简化处理P=Fr。由于仅分析其静力学性能，故选用额定静载荷作为径向载荷，以面载荷的形式施加在加载板上的一个圆形区域内，圆的直径为10 mm。

对关节轴承设置边界条件时，在不影响试验数据的前提下，根据实际工况，将心轴的两端完全固定。由于该机构没有底座支承，为防止心轴弯曲过大，将加载板外圆环面设置为全约束。自润滑关节轴的载荷及约束设置如图2所示。因轴承只承受径向载荷(图中对应z方向)，所有变形均为对称分布，故可不设置零件x，y方向的位移约束。

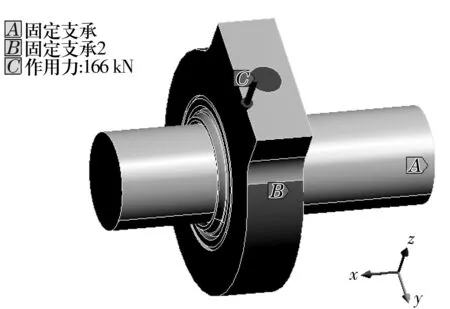
图2 自润滑关节轴承边界条件

3 分析计算与讨论

根据上述有限元模型和边界条件的设置，得到自润滑向心关节轴承von Mises等效应力分布如图3所示。外圈最大von Mises等效应力出现在外圈外侧边缘上，为551.42 MPa。而衬垫的最大等效应力出现在边缘靠内1～2 mm处，这是由于内圈比外圈宽，同时由于受外圈内侧倒角的影响，在径向载荷作用下，使衬垫边缘产生应力集中。

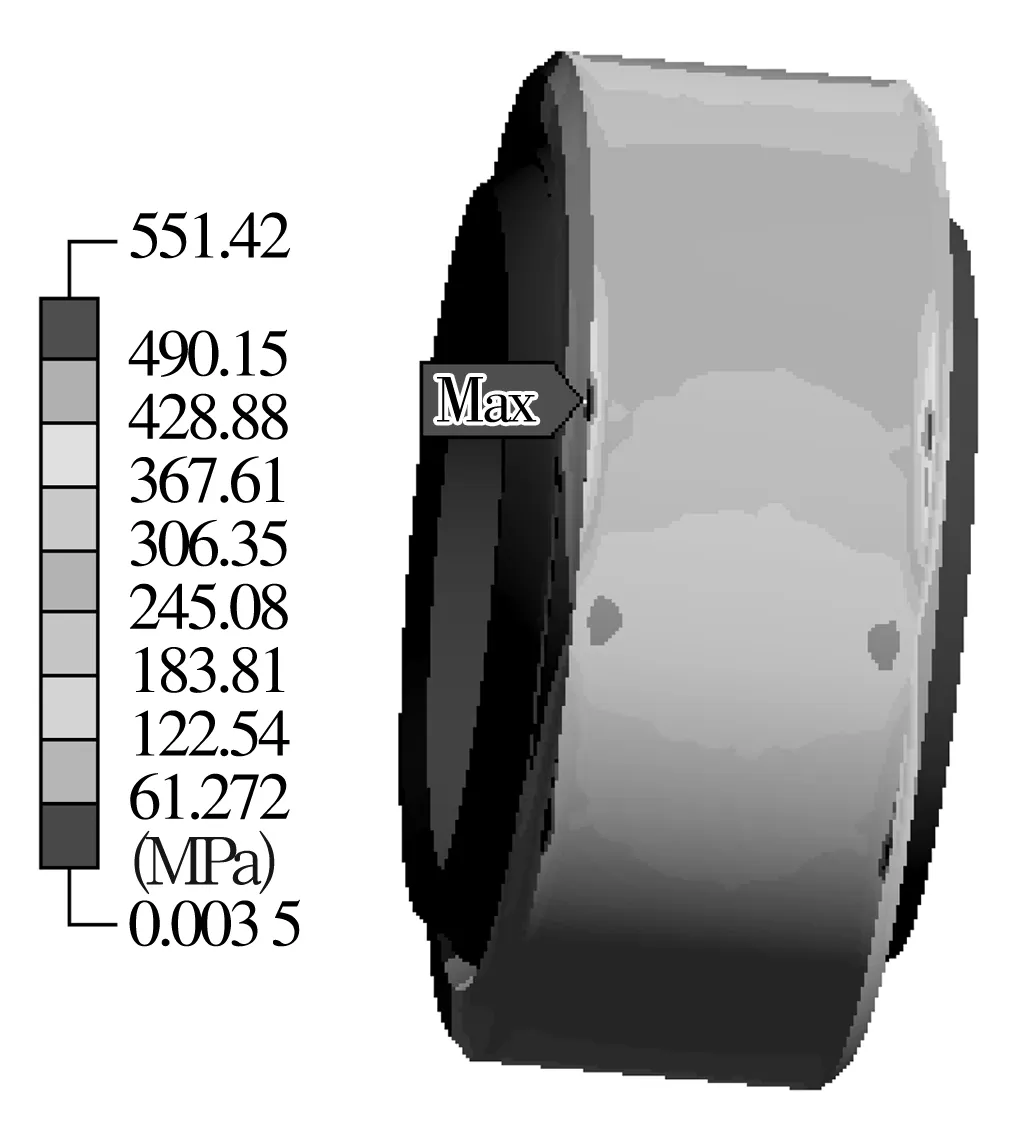
图3 关节轴承Mises应力分布图

关节轴承在径向载荷作用下的位移如图4所示(z向为载荷作用方向)，最大位移约为0.054 mm，出现在衬垫层的边缘上。内圈宽度大于外圈宽度，在受到径向载荷作用时，衬垫外侧会产生应力集中，由于衬垫材料的弹性模量较小，容易产生变形，向外圈外侧凸出，故位移最大值出现在外圈边缘处；外圈最大变形出现在径向载荷作用中心点的轴向上，且向圆周两边逐渐减小；内圈最大变形出现在表面中心处，最大值约为0.008 4 mm。

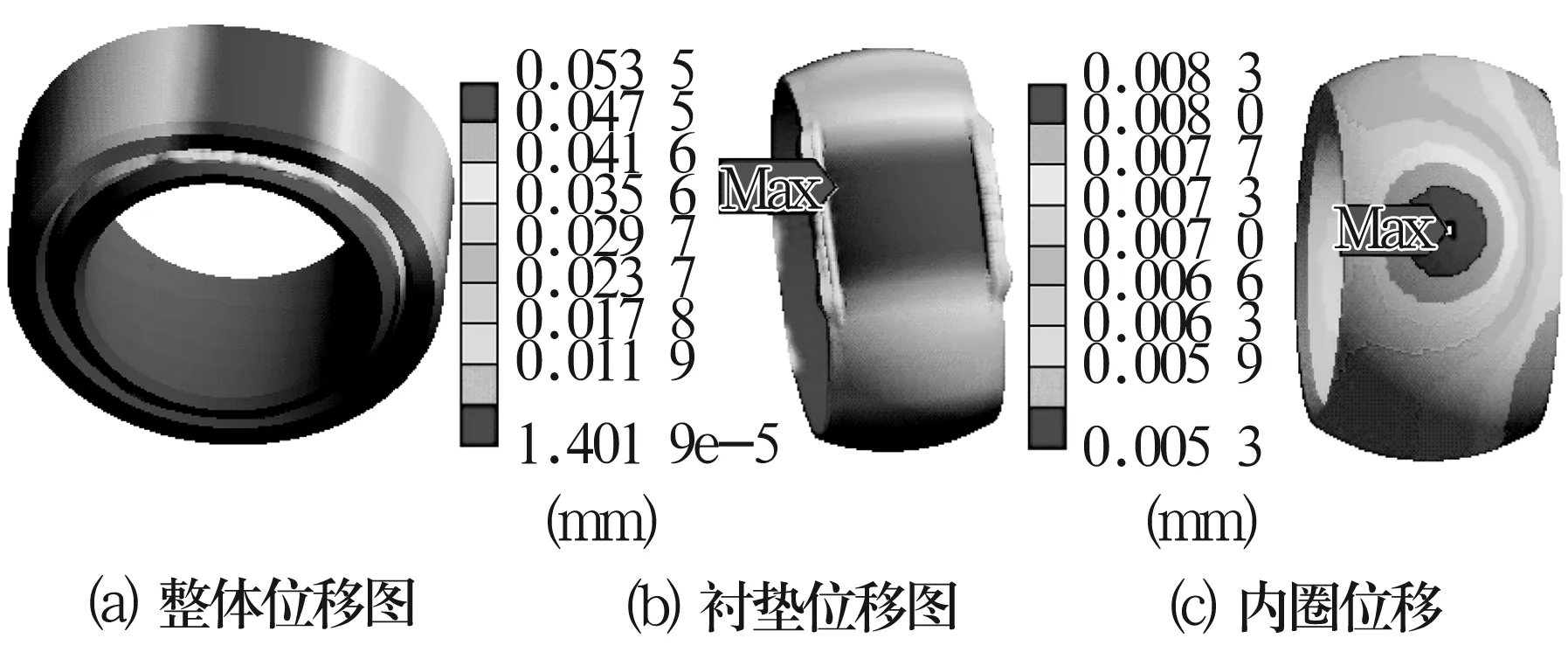
图4 关节轴承径向位移分布图

对向心关节轴承进行优化设计和结构分析时，轴承衬垫层与内圈之间的接触应力非常重要。轴承在转动和摆动过程中，接触应力对2球面间的摩擦力及接触面间的磨损起决定性作用，从而直接影响轴承的总体性能和寿命。图5为自润滑向心关节轴承衬垫层与内圈之间的接触应力分布。

图5 关节轴承衬垫接触应力分布图

从图5可以看出，衬垫层与轴承内圈之间的最大接触应力主要集中在径向载荷方向的中心处，最大值为88.554 MPa，衬垫磨损最严重位置出现在载荷中心附近，并向两侧递减。衬垫内侧接触应力在径向载荷中心z=0，并沿圆环切线方向(y方向)-20～20 mm变化时的接触应力分布情况如图6所示，基本呈抛物线形状，与文献[4]分析的在没有衬垫情况下，关节轴承内、外圈接触面上的接触应力分布基本一致。

图6 关节轴承衬垫接触应力趋势图

衬垫是自润滑关节轴承实现自润滑的关键部分，当采用不同衬垫材料时，对轴承性能及使用寿命将产生不同的影响。因此，在对自润滑关节轴承进行静力学分析时，有必要对不同衬垫材料的关节轴承进行对比分析。在此通过不改变材料的泊松比和密度，同比例增加衬垫材料的弹性模量，分析衬垫的变形量与接触应力的变化情况。以前述衬垫材料的弹性模量为基数，分别以2，4，8，16，32倍基数的衬垫材料弹性模量进行分析，得出相对应衬垫的最大位移和最大接触应力，趋势如图7所示。

由图7可以看出，随着弹性模量的增大，衬垫变形(位移)逐渐趋缓，而衬垫的接触应力基本呈线性增大趋势。以二硫化钼填充聚四氟乙烯复合材料为例，增加二硫化钼填充比例时，会增加复合材料的弹性模量和材料硬度，提高材料耐磨性，材料受载不易变形；但随着二硫化钼填充比例的增加，衬垫复合材料的摩擦因数和接触应力提高，从而加速衬垫磨损。

不同材料的最佳配比是不同的，因此，需要对填充材料的填加比例进行不断试验探索，以获得适宜的填充比，使复合材料的耐磨性能达到最佳。