基于形态分形维数与改进ELM的轴承故障预测

2014-07-21陈强华李洪儒许葆华

轴承 2014年4期

陈强华，李洪儒，许葆华

(军械工程学院，石家庄 050003)

轴承作为旋转机械的关键部件，对系统的正常运行起着非常重要的作用。据统计，齿轮箱故障中19%由轴承故障引起[1]，在泵与电动机中，这一比例更是高达51%[2]，如何对轴承将出现的故障进行准确预测，防止重大损失，是目前研究的重点和热点。

故障预测一般分为2个步骤，即故障特征提取和故障预测。其中，故障特征提取是故障预测的基础和关键。有效的特征量可以较好反映轴承性能退化的整个过程，为故障预测提供可靠依据。目前，主要有循环平稳分析[3-4]、小波包分解的节点能量分析[5]以及小波相关特征尺度熵分析[6]等故障特征提取方法。

分形理论为复杂信号的分析提供了十分简单的方法，被广泛应用于地理、生物、材料及计算机等领域[7-8]。近年来，许多学者将该理论应用于故障特征提取与故障诊断领域，并取得了较好的效果[9-11]。分形维数(Fractal Dimension，FD)作为分形体的重要特征量，用以描述分形体的不规则性和自相似性，可以定量反映设备在不同状态下的分形特征。文献[12]将数学形态学应用到分形维数的计算中，大大简化了分形维数的计算，并提高了精度和稳定性。

极限学习机(Extreme Learning Machine，ELM)是一种单隐层前馈神经网络[13]，其将神经网络的参数训练问题转化为线性方程组的求解，经过一次计算求得方程的最小范数二乘解，并将其作为神经网络的权值。因此，ELM较传统的神经网络具有更快的训练速度和更好的泛化能力[14]，并在时间序列预测、模式识别和在线监测中获得了成功应用[15-17]。然而，由于ELM在应用过程中随机给定左侧权值，其在模型精度和稳定性方面不甚理想。

在此，较详细阐述了利用数学形态学计算信号单重分形维数的方法，并将其应用到故障特征提取中，将形态分形维数作为轴承故障预测的特征量，以反映轴承性能退化的过程。在故障预测方面，针对ELM存在的不足，给出一个序列关联度系数综合衡量模型的精度与稳定性，并利用该参数对ELM模型进行优化。通过提取的故障预测特征对优化的ELM预测模型进行训练，验证了形态分形维数作为故障预测特征的有效性，以及改进ELM预测模型在轴承故障预测稳定性和精度方面的改善。

1 基于形态分形维数的轴承故障预测特征提取

1.1 分形维数

传统的欧氏几何认为，几何形体的维数均为整数。而实际应用中，自然界大部分几何形体的维数都呈分数形式，使得这种观念存在很大的局限。因此，提出了分形维数，将欧氏几何无法解决的复杂几何形体的分形特征进行了量化。目前，已有多种不同的分形维数用以度量物体的分形特征，如Hausdorff维数、Lyapunov维数、自相似维数、盒维数、信息维数及关联维数等。

由于不同的信号具有各异的分形特征，可以根据信号在分形特征上存在的差异性对其进行区分。在故障诊断中，不同故障模式信号的分形维数表现出一定的差异性，可用于度量不同故障模式下信号的分形特征，从而区分不同的故障特征，实现故障诊断。轴承劣化过程中，不同阶段信号的分形维数亦存在差异性[6]，因此，将分形维数引入轴承劣化过程的特征提取可以实现轴承故障的预测。

在机械故障研究领域，盒维数及关联维数被普遍应用。其中，关联维数计算复杂，特性较难准确把握，因此，盒维数的应用更为广泛。一般，计算分形维数的基本思想是利用不同尺度几何形状的集合对分析对象进行度量。盒维数是通过计算覆盖一个信号所需的最小盒子数得到。若以利用边长为ε的方格完全覆盖信号所占的区域需要N(ε)个方格，则信号的盒维数为

(1)

盒维数的计算是以规则的方格对不规则的信号进行覆盖，这种方法在计算过程中将产生不小的误差，影响对分形维数的计算[18]，故将形态学方法引入分形维数的计算中[12]。

1.2 故障特征提取

数学形态学基本运算主要有腐蚀和膨胀。设f(n)和g(m)分别是定义在集合F={0,1,…，N-1}和G={0,1,…,M-1}上的离散函数，且N≥M，其中，f(n)为原始信号，g(m)为结构元素，f(n)关于g(m)的形态腐蚀和形态膨胀算子分别定义为

(fΘg)(n)=min{f(n+m)-g(m)}，

(2)

(f⊕g)(n)=max{f(n-m)+g(m)}。

(3)

采用扁平结构元素g={0，0，0}对信号分别进行腐蚀、膨胀运算后得到的波形如图1所示，由图可以看出，腐蚀运算平滑了负脉冲，削尖了正脉冲；膨胀运算则削尖了负脉冲，平滑了正脉冲。

图1 不同形态学运算对信号的处理结果

对于单位结构元素g(m)，尺度s下的结构元素sg定义为

(4)

可以看出，sg为g经过s-1次自身膨胀所得，形态学运算中的多尺度运算与分形维数计算的基本思想一致。取不同尺度ε对信号进行覆盖，由腐蚀与膨胀对信号处理后的基本特点可知，形态膨胀与形态腐蚀对信号进行处理后的差值可以将信号进行覆盖，定义覆盖面积为

(5)

则不同尺度ε下覆盖面积与尺度间的关系为[12]

lg(Ag(ε)/ε2)=DMlg(1/ε)+c，

(6)

式中：DM为信号的Minkowski-Bouligand维数，只要对不同尺度下计算得到的lg(Ag(ε)/ε2)与lg(1/ε)值进行最小二乘线性拟合，即可得到Minkowski-Bouligand维数的估计。为兼顾估计精度和计算效率，选择长度为3的扁平结构元素为基本结构元素，并取尺度范围为1～64。

根据形态分形维数的定义和计算方法可知，形态分形维数反映了振动信号的峰值在整个信号中概率分布的不均匀程度，定量表征了轴承故障振动信号的形态特征和振动的剧烈程度。因此，可利用形态分形维数的这些性质，结合轴承性能退化的特点，将其作为轴承故障预测的特征量，定量反映轴承性能退化过程中振动信号的变化。

2 基于改进ELM的轴承故障预测方法

2.1 ELM基本原理

给定一个含N个样本的训练集T={(xi,yi)|xi∈Rm;yi∈Rn;i=1,2,…,N}，则具有L个隐层神经元的ELM输出可以表示为

(7)

式中：βt为连接第t个隐层结点的输出权值向量；at为连接第t个隐层结点的输入权值向量；bt为第t个隐层神经元的阈值；f(x)为隐层神经元的激活函数。

将(7)式写成线性方程组的形式为

Hβ=Y，

(8)

β=[β1,β2,…,βL]T；Y=[y1,y2,…,yN]T。

若隐层输出矩阵H满足L≤N，那么(8)式中β具有最小二乘解，即

β=H+Y，

(9)

式中：H+为H的Moor-Penrose广义逆矩阵。

综上可知，ELM在训练过程中无需像传统神经网络那样反复迭代、调整隐层神经元权值和阈值，在隐层结点确定的情况下，只需一次计算即可获得方程最优解，这使得ELM的训练速度大大提高，且不易陷入局部最优[15]。但是，由于ELM在训练过程中随机确定隐层权值和阈值，使其在模型精度和稳定性方面不甚理想，且与其他神经网络一样存在过拟合现象。

2.2 基于改进ELM的轴承故障预测方法

传统的优化方法一般仅采用模型的误差作为目标函数，对模型进行优化。但在预测过程中，模型预测序列与训练样本变化趋势的一致性以及模型的稳定性往往受到忽视。因此，提出了一种序列关联度指标，综合考虑ELM的性能，对ELM进行优化。

设原数据序列为X={xj|j=1,2,…,n}，预测值序列为X1={xj′|j=1,2,…,n}，定义趋势变化相关系数为

(10)

该系数反映了2个序列之间各个对应点变化趋势的一致性，该系数越大，则2个序列变化趋势一致性越好。

(11)

其中，pj为第j个点的预测值与原始值之间相对误差的比重，即

(12)

误差序列的熵值反映了模型的稳定程度，该值越大，表示误差序列的变异度越小，模型的预测越稳定。反之，模型的预测越不稳定[19]。综上，定义预测值与原始值2个序列的序列关联度系数为

(13)

式中：σ为误差的方差。该系数综合考虑了模型的精度、稳定性以及预测序列与原始序列变化趋势的一致性。

为求得ELM隐层输入权值和阈值的最佳值，采用粒子群优化算法对权值和阈值进行寻优。利用输入权值和阈值组成种群中的个体，即

Xj={aj1,aj2,…,ajL,bj1,bj2,…,bjL}T。

(14)

其中，所有输入权值和阈值均在[-1,1]范围内随机产生。模型的输出权值可以由(9)式计算得到。粒子群的适应度函数采用上述的序列关联度系数ξ。

利用上述方法对ELM进行改进，通过前一小节提取的轴承故障预测特征序列对优化后的ELM预测模型进行训练，确定改进的ELM预测模型的左侧权值和阈值，根据(9)式确定模型的输出权值向量。改进的ELM预测模型经过训练后，即可用于轴承故障的预测。

3 轴承故障预测与验证

为验证上述轴承故障预测方法的效果，采用实测的轴承振动加速度全寿命数据进行验证。该全寿命数据来自IMS中心轴承试验台。如图2所示，该试验在同一个轴上安装4套ZA-2115双列滚子轴承，并通过一个弹簧机械装置在轴承径向加载。通过电动机将轴驱动至2 000 r/min，每隔10 min采样一次，采样频率为20 kHz，采样长度为20 480个点。试验运行一段时间后，因轴承1出现外圈故障而停止采样，共采得984组数据。

3.1 轴承故障预测提取

轴承1振动波形的均方根值(RMS)与峰峰值(P-P)随着轴承劣化的变换曲线如图3所示，可以看出这2个值随着轴承劣化逐渐增大，但波动较大。若以此为特征量对轴承故障进行预测，将增加预测的难度。因此，采用形态分形维数作为故障预测特征量对轴承故障进行预测。

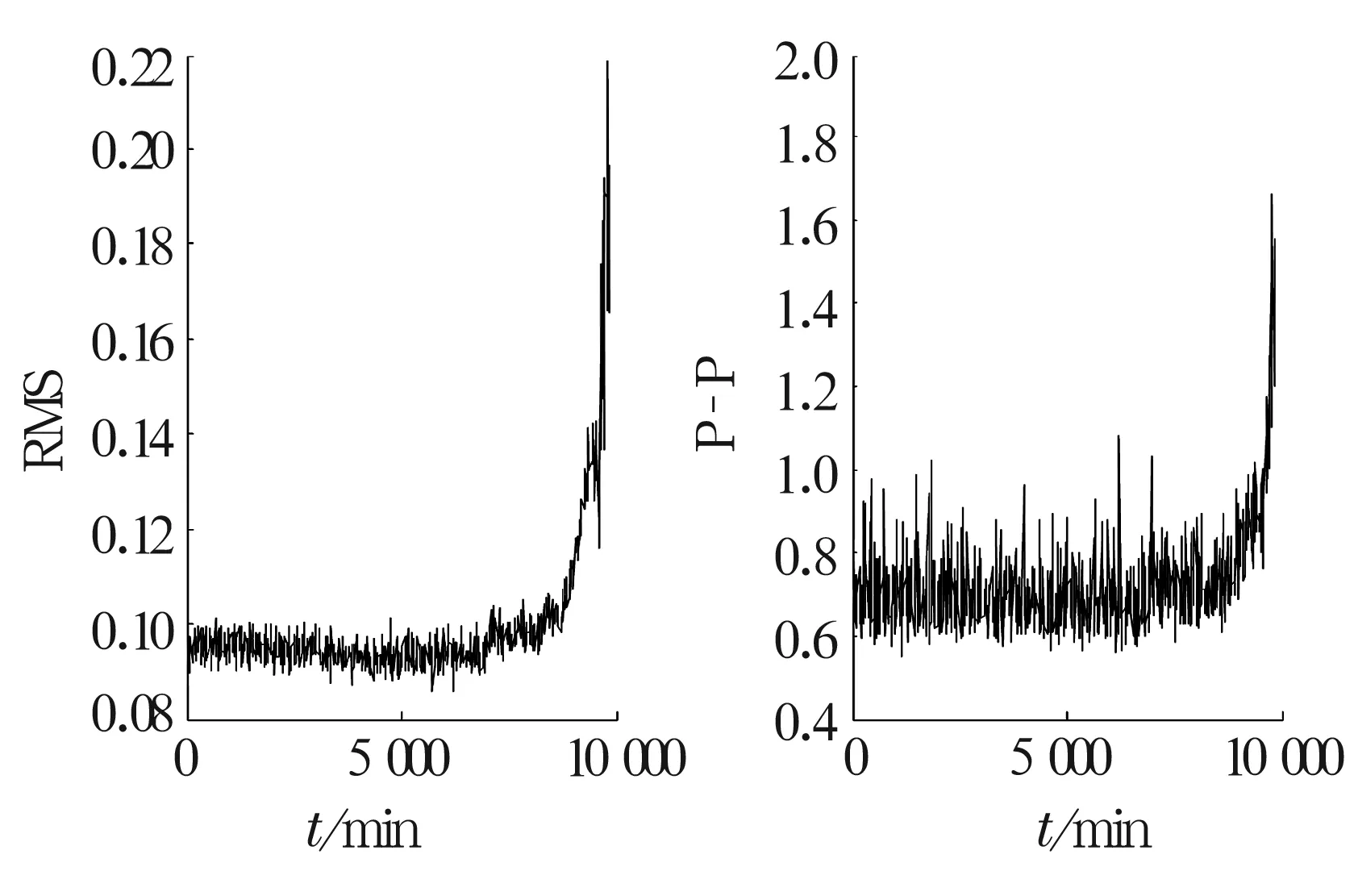
图3 RMS与P-P值随故障的变化趋势

任取其中一组数据，计算其形态分形维数，求取形态分形维数而拟合的曲线如图4所示，其中尺度范围为1～64，图中曲线的斜率即为该组数据的形态分形维数。

图4 lg(1/ε)与lg(Ag(ε)/ε2)的拟合曲线

在所有的数据中，取第651～980组数据分别计算每组数据的形态分形维数，并做出其随时间变化的曲线，如图5所示。在第8 570 min之前，MFD值一直在1.76附近小幅波动，轴承处于正常工作状态。此后，MFD值随着时间逐渐减小，反映了轴承随着时间劣化的过程，说明了形态分形维数作为故障特征对轴承进行故障预测的可行性。

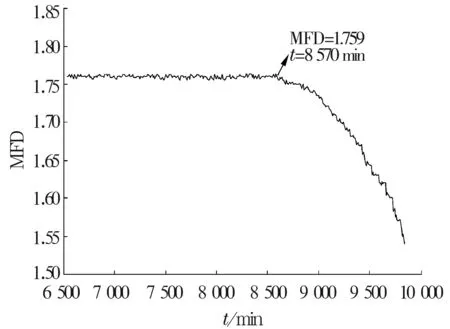
图5 MFD随故障演化趋势

3.2 轴承故障预测方法

取第8 560 min之后的100个点作为训练样本对改进ELM进行训练，并将其之后20个数据作为测试集，利用训练得到的ELM预测模型对后20个数据进行预测，ELM改进前、后的预测结果如图6及表1所示，可以看出改进ELM的预测结果与原数据序列变化的趋势一致性更好，改进ELM预测模型具有更高的预测精度及稳定性。