基于ANSYS的推力永磁轴承磁力特性研究
2014-07-21张坚孙玉卓张海龙孟庆涛张钢
张坚,孙玉卓,张海龙,孟庆涛,张钢
(上海大学 机电工程与自动化学院,上海 200072)
永磁轴承具有微摩擦、低功耗、无污染、高转速、无需润滑和密封等一系列优良特性,具有广阔的应用前景。由Earnshaw定律可知,永磁轴承不能实现所有自由度的稳定悬浮[1]。因此,在永磁悬浮系统中,至少在1个自由度上需引入其他主动支承方式,可与电磁轴承、机械轴承等相结合,构成各种形式的磁轴承系统。近年来,随着稀土NdFeB永磁材料的飞速发展,国内、外学者对永磁轴承做了大量的研究,其中尤以永磁轴承承载能力和刚度的研究为甚。到目前为止,研究方法主要有等效磁荷法[2-4]、分子电流法[5-6]、矢量磁位法[7]、虚位移法[8-9]和有限元法[10-11]等。试验研究表明,永磁轴承的承载能力和刚度计算的有限元数值解与试验结果较为吻合[12-13]。但目前对推力永磁轴承的研究多而不全,有待充实。因此,在此对推力永磁轴承的磁力特性进行有限元分析,以期得出其承载力、刚度与磁环结构参数之间的关系,对该轴承的结构优化设计提供帮助。
1 推力永磁轴承结构
Yonnet提出采用径向磁化及轴向磁化的磁环可构成多种结构的轴向永磁轴承[14],如图1所示。
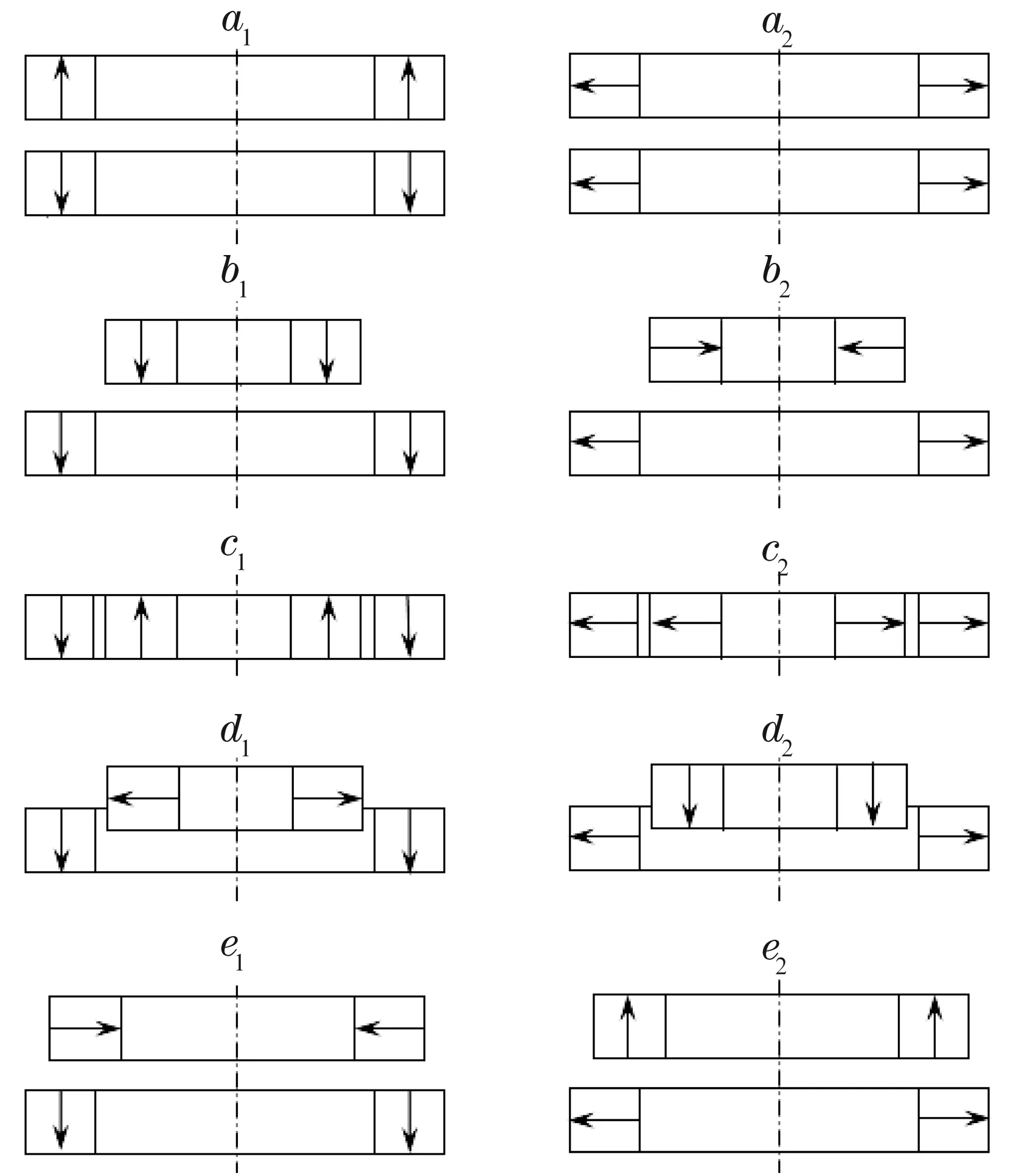
图1 轴向永磁轴承单元结构
在实际制造中,径向磁化比较难实现,而轴向磁化则较为普遍,因此在设计永磁轴承时,应选择轴向磁化的永磁环。另外,图1中a1型永磁轴承单元结构简单,安装方便,且当上、下两磁环的端面重合时能产生较大的轴向力,而径向方向上的不稳定力较小,适合做斥力型轴向轴承。故文中以此类型永磁轴承单元作为基本结构组成一种推力永磁轴承,其结构如图2所示,该轴承主要用于承受轴向载荷。

1—辅助滚动轴承;2—轴内圈;3—上定磁环;4—动磁环;5—下定磁环
图2所示推力永磁轴承在轴内圈两端各安装了一个辅助滚动轴承,用以对其径向自由度进行定位约束。故该轴承内两定磁环对动磁环所产生的径向载荷均由辅助滚动轴承来承担,即
Fr=Fr1+Fr2,
(1)
式中:Fr为辅助滚动轴承对轴内圈的作用力;Fr1,Fr2分别为上、下定磁环对动磁环的径向作用力。
由(1)式可知,只要辅助滚动轴承安装精确,就能保证动磁环的对中性,从而实现Fr=0。即动磁环在径向上不再产生位移,其径向力和径向刚度则可忽略不计,因此仅对其轴向承载力和轴向刚度进行研究。
该推力永磁轴承的工作原理为:工作时,轴上施加外载荷Fz,动磁环同轴内圈产生向下的位移z,致使动磁环与下定磁环间的气隙变小,下定磁环对动磁环的磁力Fz1(方向向上)相应增大,而动磁环与上定磁环间的气隙变大,上定磁环对动磁环的磁力Fz2(方向向下)相应减小。随着轴向位移的增加,两磁力之间的合力增大,当合力等于外载荷时,轴和动磁环在轴向上处于稳定悬浮状态。因此,轴向外载荷Fz和轴向刚度Kz分别为
Fz=Fz1-Fz2,
(2)
Kz=dFz/dz。
(3)
2 轴承的磁力分析
2.1 有限元模型的建立
虽然推力永磁轴承是三维的,但只考虑轴向位移且磁环为轴对称结构,故在实际计算中可以将其简化为二维平面问题,使用轴对称二维模型,这样可以在减小计算量的同时得到较高的计算精度。因此,文中取其1/2截面结构模型,并建立rz二维坐标系,r,z向分别为径向和轴向,具体结构尺寸如图3所示。图3中H,L分别为定磁环厚度和宽度;h,l分别为动磁环厚度和宽度;g为磁环之间的平均气隙;Rf为磁环的平均半径(磁环内半径和外半径的平均值)。
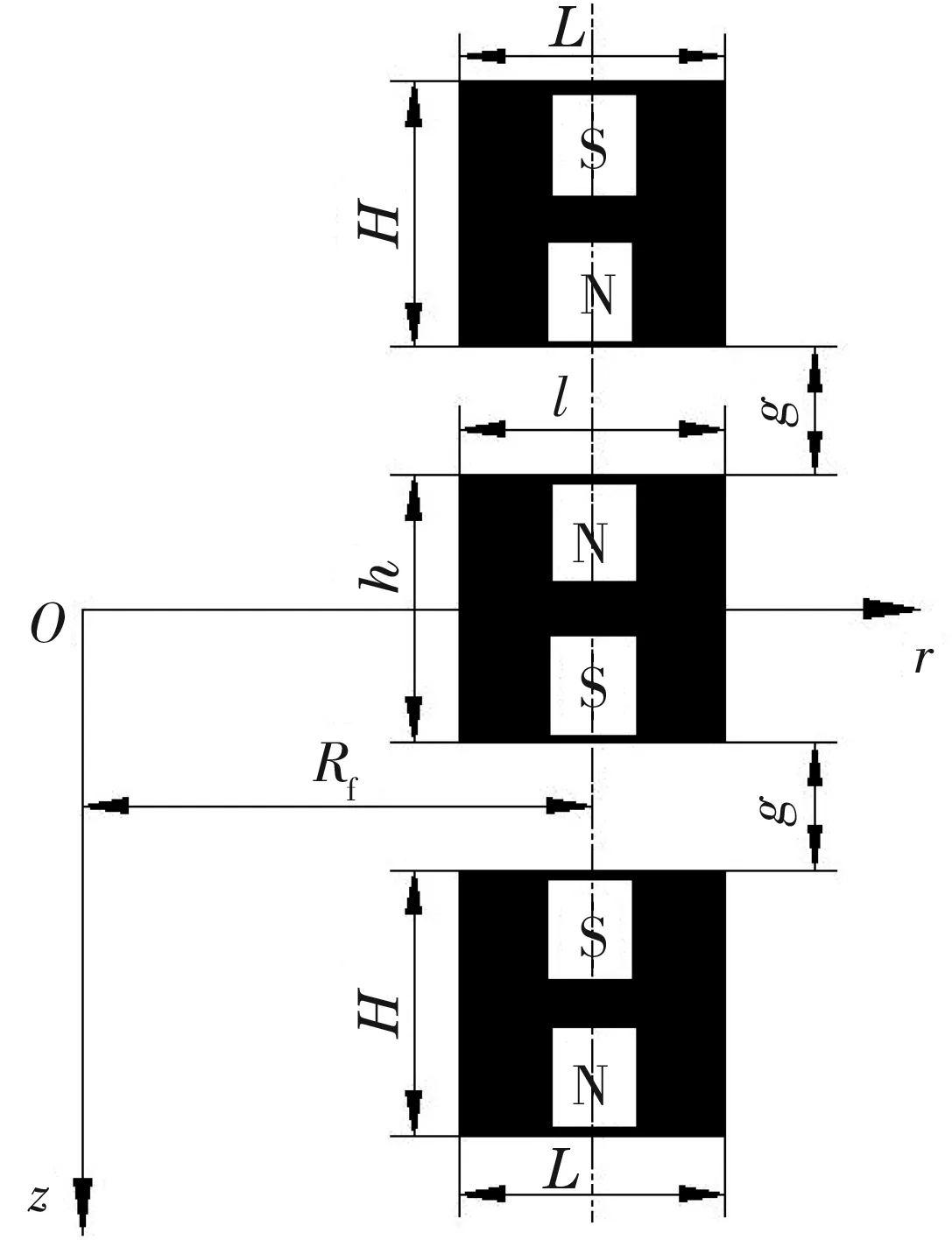
图3 推力永磁轴承1/2截面模型
基于此,在ANSYS中建立xz平面(r轴在ANSYS中由x轴来体现)的二维模型,并考虑漏磁的存在。选用PLANE53为轴对称单元,主要用于内部空气和其所包络的磁环;选用INFIN10单元用于最外层的空气远场,这可以得到更精确的磁力值。空气的相对磁导率设置为1,磁环的材料则通过设置Hc和μr来完成。由于磁环材料采用N35型NdFeB,根据实验室所定制的磁环测得:Hc=922 880 A/m,Br=1.210 6 T。由于真空磁导率μ0=4π×10-7H/m,故磁环的相对磁导率μr=Br/(μ0Hc)=1.044 3。
2.2 网格划分
由于网格的精度对结果影响较大,这里对磁环采用映射网格划分,并对磁环截面的两相邻边进行线单元尺寸设置。由于以上有限元模型是在MKS单位制下建立的,取“Element edge length”的值为0.001 m。而相对磁环来说,空气和远场作为包络场,其对网格所要求的精度不高,故对其进行自由网格划分,并设置面单元边长为0.002 m。
2.3 加载求解
在研究推力永磁轴承内部的磁场分布时,暂不考虑其向外的漏磁,因此在模型最外层加上磁力线平行边界条件,即令Az=0。另外,由于需计算动磁环所受到的磁力,故将动磁环单元定义为一个组件,并给动磁环加上力边界条件。接下来选择求解器,确定分析类型为静态分析,启动求解器进行求解。
2.4 后处理
在通用后处理器POST1中查看推力永磁轴承磁力分析结果。图4和图5分别为Rf=44 mm,g=2 mm,H=h=L=l=12 mm的推力永磁轴承在轴向位移为0.8 mm时的磁力线分布图和磁通密度云图。
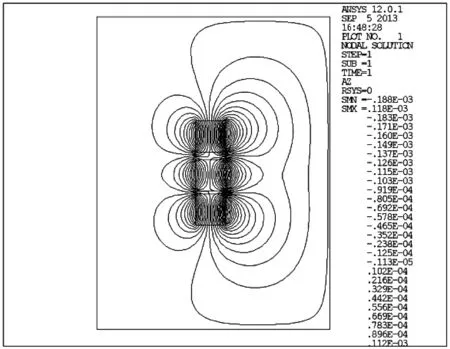
图4 轴向位移为0.8 mm时的磁力线分布图

图5 轴向位移为0.8 mm时的磁通密度云图
最后需要注意的是,ANSYS通过虚位移法和MAXWELL法分别计算磁力,两者计算结果会有微小的差异,如果差别较大,就应考虑修改网格划分的精度或方法。而通过ANSYS对该算例的永磁轴承进行仿真计算可知,由虚位移法得到的磁力为204.17 N,由MAXWELL法得到的磁力为199.89 N,两者相差仅2.14%,小于5%,故本算例所建模型的网格划分较合理。
3 轴承结构尺寸分析
考虑到实验室对磁环的使用情况以及动、定磁环整体尺寸的变化,这里取Rf为定常数,Rf=44 mm。另外,为了保证动磁环在静止状态下始终处于稳定悬浮状态,则上、下定磁环的结构参数取值应完全相同。分别分析动、定磁环宽度、厚度、截面积和气隙对推力永磁轴承磁力特性的影响。
3.1 动、定磁环宽度的影响
取g=2 mm,H=h=12 mm。为了合理分析动、定磁环宽度对轴承轴向承载力和轴向刚度的影响,分别对L≠l和L=l的情况进行分析。当L≠l时,取l=12 mm,L=6,9,15,18 mm,即L/l∈{0.5,0.75,1.25,1.5},分析其承载特性并与L/l=1(L=l=12 mm)下的结果进行对比,如图6所示。而当L=l=6,9,12,15,18 mm时的磁力特性分析结果如图7所示。
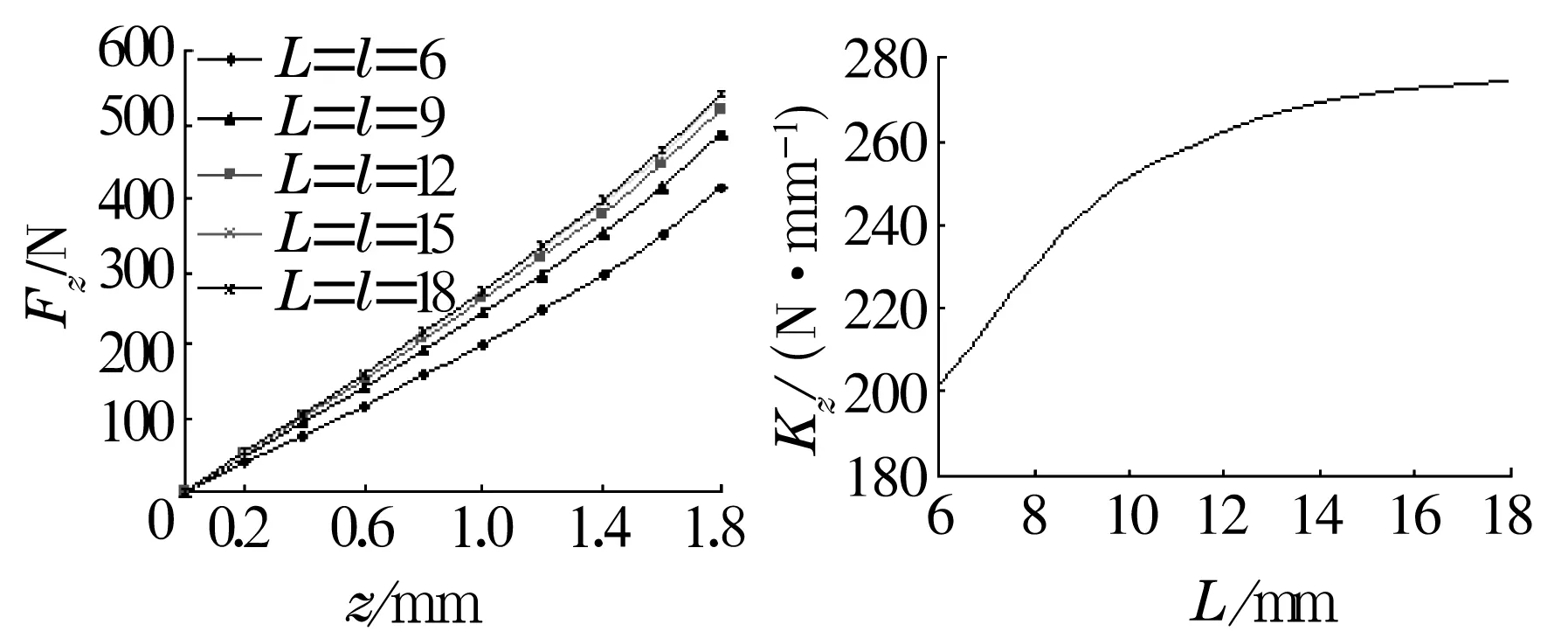
图7 L=l时推力永磁轴承轴向磁力特性
由图6可知,当L≠l时,二者的值越接近,推力永磁轴承的轴向刚度越大;当L=l时,轴向刚度达到最大。由图7可知,在L=l时,轴向承载力和轴向刚度随着L的增大而增大;但当L>H以后,随着L的增大,轴向承载力和轴向刚度几乎无变化。因此,当磁环宽度等于其厚度时,再通过增加磁环的宽度来提高轴向承载力和轴向刚度并不能起到理想的效果。
3.2 动、定磁环厚度的影响
取g=2 mm,L=l=12 mm。当H≠h时,取h=12 mm,H=6,9,15,18 mm,即H/h∈{0.5,0.75,1.25,1.5},分析其承载特性并与H/h=1(H=h=12 mm)时的结果进行对比,如图8所示。而当H=h=6,9,12,15,18 mm时的磁力特性分析结果如图9所示。

图8 H≠h时推力永磁轴承轴向磁力特性

图9 H=h时推力永磁轴承轴向磁力特性
由图8可知,当H
3.3 动、定磁环截面面积的影响
根据上述分析,在实际使用过程中,为了使永磁环之间能产生较为理想的磁力,一般取磁环的厚度与宽度相等,即磁环的截面为正方形(面积为a2,a=H=L=h=l)。取g=2 mm,a=6,9,12,15,18 mm时,磁力特性分析结果如图10所示。
由图10可知,轴承的轴向刚度随着a的增大而增大,且增大幅度逐渐放缓。另外,随着轴向位移z的增大,其轴向刚度也有增大的趋势。因此,在设计推力永磁轴承时,合理选择截面面积显得十分必要。
3.4 动、定磁环间气隙的影响
取H=h=L=l=12 mm,g=1,2,3,4 mm时,磁力特性分析结果如图11所示。
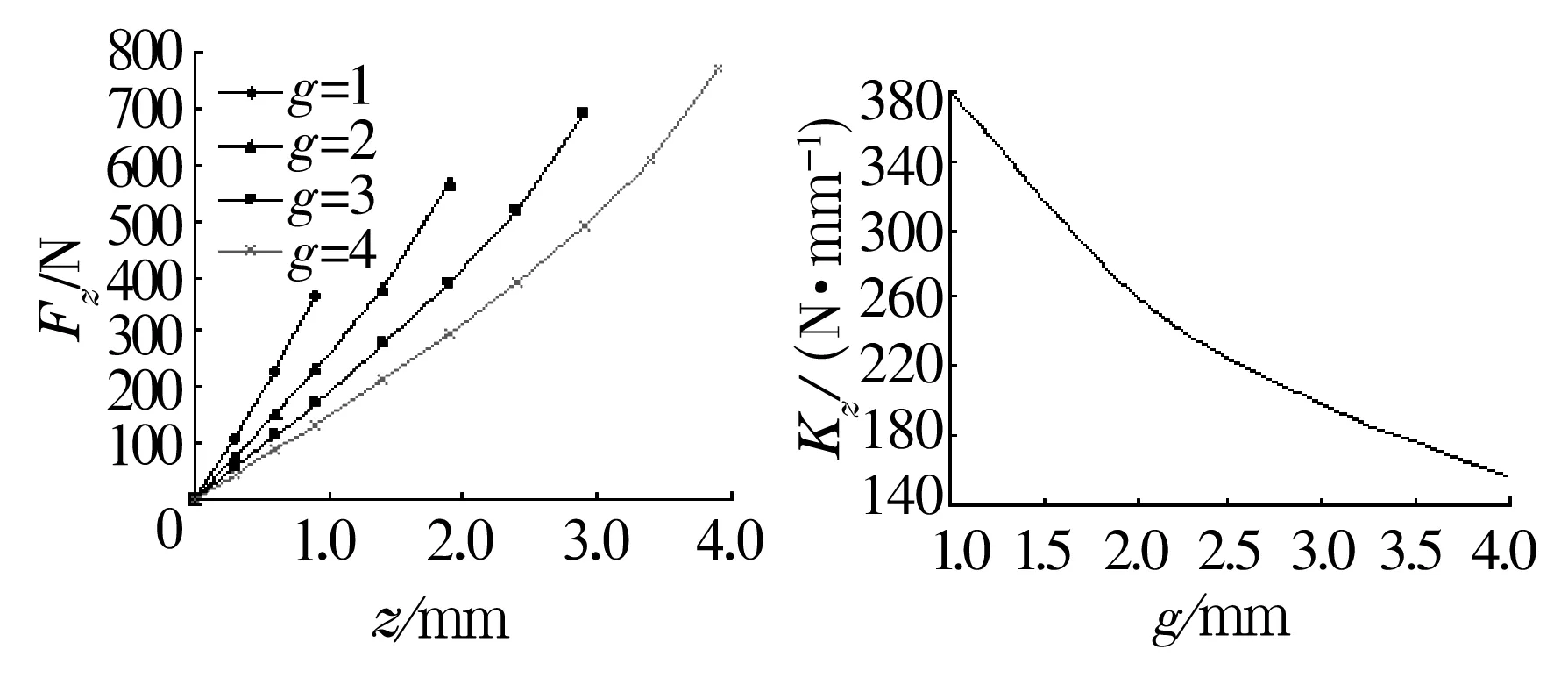
图11 气隙g对永磁推力轴承轴向磁力特性的影响
由图11可知,随着g的减小,轴承的轴向刚度变大,且线性愈合程度越佳;但轴承的轴向承载力却急剧减小。因此,在设计推力永磁轴承的气隙时,需综合考虑最大轴向承载力和轴向刚度的影响。
4 结论
在Rf一定的情况下,推力永磁轴承的设计主要取决于H,h,L,l和g,通过上述分析得出以下结论:
(1)动、定磁环的宽度最好相等或相近,具体取值需以磁环的平均半径Rf为基准,以满足推力永磁轴承的轴向刚度为目标;
(2)动、定磁环的厚度最好相等或相近,具体取值当以磁环的宽度为参考标准,当厚度和宽度相等时,推力永磁轴承的磁力和刚度能处于较理想状态;
(3)推力永磁轴承磁环的截面为正方形或近似正方形为宜,轴承的轴向承载力和刚度在其面积增大到一定值时变化较小,因此,设计满足承载刚度的磁环截面面积即可;
(4)推力永磁轴承的气隙设计需视工况而定,主要参考工况载荷和刚度。
