单因素方差分析应用的实证研究

高卓

（华南农业大学珠江学院，广东 广州 510900）

单因素方差分析应用的实证研究

高卓

（华南农业大学珠江学院，广东 广州 510900）

单因素方差分析用于完全随机设计的多个样本均值间的比较，其统计推断是推断各样本所代表的各总体均值是否相等.通过实例来完成单因素方差分析，并分析了单因素方差分析的优点和缺点.

单因素方差分析；总体；均值

1 引言

20世纪20年代英国统计学家R.A.Fisher首次引入方差分析，它是通过分析数据的误差来源检验多个总体的均值是否相同，也就是给出一个或多个自变量对因变量是否独立的初步判断.可以根据自变量的个数将方差分析分为单因素方差分析和双因素方差分析.方差分析的理论简单，但计算量相对比较大，然而随着计算机的迅速发展，方差分析日显其优势，在经济学、生物学、医药学、社会学等多方面都得到了广泛应用.

2 单因素方差分析原理

为了方便，先看一个实例，表1是2011级某班一二年级的高等数学（上、下）、线性代数、概率论与数理统计四门大学数学课程的成绩，试分析该班的四门课成绩有没有显著差异.

本例中要检验的因素是四门大学数学课程成绩，用A表示，因素下的四个分类型变量分别为高等数学（上）、高等数学（下）、线性代数和概率论与数理统计四个总体称为因素的四个水平，用Aj表示，xij称为第j个水平的第i个观测值.方差分析就是从数据的误差来源来分析多个总体的均值是否相等，在本例中就是指高等数学（上）、高等数学（下）、线性代数和概率论与数理统计这四个总体的均值是否相等.

一般地，在单因素试验中，假设实验因素A有s个水平A1,A2,…,As，在水平Aj(j=1,2,…,s)下进行nj(nj≥2)次独立试验.建立如下假设：

H0:μ1=μ2=…=μs,H0:μ1,μ2,…,μs不全相等.

每个总体系统内部的误差，主要是由随机抽样所引起的随机误差，称为组内误差，组内误差平方和，记为SSA：

各总体之间的误差，主要是由随机抽样引起的随机误差和系统误差，称为组间误差，组间误差平方和记为

数据总的误差平方和记为SST：

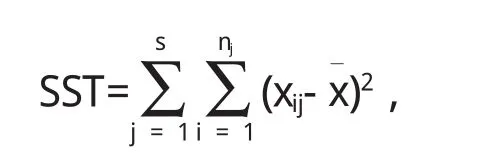
其中，xij表示第j个水平的第i个观测值，x¯·j表示水平Aj下的均值，x¯表示全部数据的总均值.

总的误差平方和可分解为：

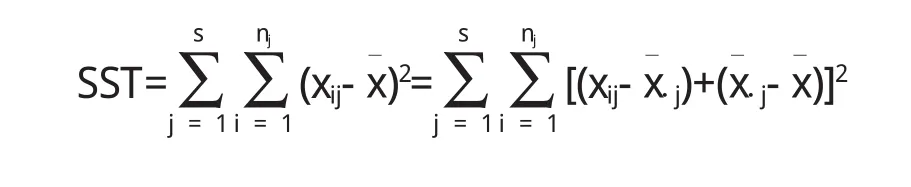
表1

这是因为上式中交叉项

上述证明表明数据总的误差主要来自两方面，一方面是组内误差，另一方面是组间误差.可以证明，当s个总体的均值相等时n-s).F值越大说明在总方差中，组间方差波动越大，s个水平的均值相差越大，越有利于拒绝s个总体均值相等的假设；F值越小，说明总方差中，组间方差波动越小，方差的波动主要是由随机误差引起的，越有利于接受s个总体的均值相等的假设.如果规定显著性水平为α，当F>Fα(s-1,n-s)时，拒绝原假设，F

3 单因素方差分析应用实例

对于上述实例，假如给定显著性水平α=0.05,我们首先求出四个因素的样本均值分别为·1= 71.422=67.883=74.14=88.16，可以看出因素的四个总体均值确实有差异.

用excel中的单因素方差分析工具分析上述例题，得到如下结果（表2）：

表2 方差分析：单因素方差分析

从上面分析可以看出F=20.06776>Fα(s-1,n-s)= 2.650677.在显著性水平α=0.05下，可以相信该班四门课成绩有显著差异.

4 结束语

单因素方差分析的优点是通过比较观测变量总的误差平方和各部分所占的比例，推断自变量对因变量带来了显著影响.在总的误差平方和中，如果组间误差平方和所占比例较大，则说明因变量的变动主要是由自变量引起的，可以主要由自变量来解释，自变量给因变量带来了显著影响；反之，如果组间误差平方和所占比例小，则说明因变量的变动不是主要由自变量引起的，不可以主要由自变量来解释，自变量的不同水平没有给因变量带来显著影响，因变量的变动是由随机变量因素引起的.

单因素方差分析的基本分析只能判断自变量是否对因变量产生了显著影响.如果自变量确实对因变量产生了显著影响，也就是表明试验中各总体均值间存在显著差异，但并不意味着每两个总体均值间的差异都显著，也不能具体说明哪些总体均值间有显著差异，哪些差异不显著.有必要进行两两总体均值间的比较，以具体判断两两总体均值间的差异显著性，这就要用到多个均值两两间的相互比较的多重比较.有兴趣的读者可以查找有关多重比较的资料.

〔1〕林伟初.概率论与数理统计[M].上海:同济大学出版社,2009.153-159.

〔2〕印德中.EXCEL在方差分析中的应用[J].中国现代教育装备,2011(17):23-25.

〔3〕李玉毛.单因素方差分析在经济数据分析中的应用[J].赤峰学院学报（自然科学版）,2012,28(2): 18-19.

〔4〕贾俊平,等.统计学（第四版）[M].北京:中国人民大学出版社,2009.

〔5〕曾五一.统计学导论[M].北京:科学出版社,2007.

O213

A

1673-260X（2014）03-0004-03

华南农业大学珠江学院2012年度科技基金项目资助（HZKJ201220）