在高等代数中用类比的方法构造反例
2014-07-21薛丽红
薛丽红
(集宁师范学院 数学系,内蒙古 乌兰察布 012000)
在高等代数中用类比的方法构造反例
薛丽红
(集宁师范学院 数学系,内蒙古 乌兰察布 012000)
在学习高等代数过程中反例对问题的理解起着其至关重要作用,构造反例就成为解决问题的关键.本文介绍了构造反例的方法-运用类比的思维方法来构造反例,并通过高等代数中知识说明了该方法的实用性.
类比;反例;命题
高等代数这门课程开设在大一第一学期,它具有概念多、理论性强、抽象等特点.对于刚刚迈进大学校门的新生来说,学习高等代数有些吃力.对于这个情况我们不能忽视.我们知道反例在认知理解事物起着特殊的作用.本文介绍了构造反例的方法—运用类比的思维方法来构造反例,并通过高等代数中知识来验证该方法的实用性.本文利用该方法来构造恰当的反例,从而帮助学生更加深刻地理解掌握概念、命题、定理,提高学生学好高等代数的自信心,同时启发学生主动地构造反例,培养学生的逆向思维和创造力.
运用类比方法构造反例就是利用我们所学过的知识(如定理、命题、熟知的结论)对比新问题,对比出该问题与我们认知的不同地方,从而利用该问题的特点在新的范围内构造反例.
命题1 实对称矩阵A的所有顺序主子式大于等于零,则A半正定
分析:可供类比的定理是实对称矩阵A的所有顺序主子式大于零,则A正定.
这样我们构造反例时先保证顺序主子式大于等于零,而对于主子式来说可有正有负的,于是我们有显然满足命题条件,但A是半负定,可见结论不成立.问题就出在没有满足主子式大于等于零,于是我们放宽条件可得这样结论:
实对称矩阵A的所有主子式大于等于零,则A半正定.
命题2 设V1和V2是线性空间V的子空间,则V1YV2未必是V的子空间.
分析:可供类比的命题是设V1和V2是线性空间V的子空间,则V1IV2是V的子空间.
由子空间判定定理可知我们要考虑加法、数乘的封闭性,对集合V1YV2来说数乘的封闭性显然满足,而对加法运算我们需要验证,可构造反例:在R2中V1={(a,0)|a∈R}和V2={(0,b)|b∈R}为R2的子空间,取α=(1,0),β=(0,1)∈V1YV2,有α+β=(1,1)∉V1YV2不满足加法的封闭性,可见V1YV2不是V的子空间.
注意命题条件再加上V1⊆V2或V1⊇V2,V1YV2就会满足加法的封闭性,使得结论成立.
命题3设A、B分别为n×s、s×n矩阵,若n>s,则|λI-AB|=|λI-BA|.
分析:可供类比的命题是:设A、B为n阶方阵,则|λI-AB|=|λI-BA|.
于是我们构造反例时要满足A、B不是方阵,再分别求出它们的特征多项式.可有有于是可得|λI-AB|λ-8,显然它们的特征多项式不同,结论不成立.细心一些我们会观察到它们还是有一定关系:仅差一个因子,我们会有结论:
设A、B分别为n×s、s×n矩阵,若n>s,则|λI-AB|=λn-s|λI-BA|.
命题4设V是有限维线性空间,σ∈L(V),则V=σV⊕σ-1(0),其中
分析:对线性变换 σ我们熟知的结论dimσV+dimσ-1(0)=dimV,于是焦点成为证明V=σV+ σ-1(0)成立.我们对比熟知的结论:设V是有限维线性空间,σ∈L(V),且σ2=σ,则V=σV⊕σ-1(0),可见一般的线性变换是不能使结论成立的.显然有σV+σ-1(0)⊆V关键证明σV+σ-1(0)⊇V,这样构造反例的线性变换σ不要满足σV+σ-1(0)⊇V,于是有反例:
设V=R[x]5,V上的线性变换σ:σ(f(x))=f'(x),∀f (x)∈V,则有σV=R[x]4和σ-1(0)=R,于是可得σV+ σ-1(0)=R[x]4+R≠R[x]5,所以一般V不等于值域σV和核σ-1(0)的直和.
从这个反例观察到是值域σV不能使结论成立,但我们能找到与σV同构的子空间W能有结论.设α1,α2,…,αs是σV的一组基,σ(ηi)=αi,∃ηi∈V, i=1,2,..s,W=L(η1,η2,…,ηs),则V=W⊕σ-1(0).
命题5设A、B为正定矩阵,则A-B正定.
分析:可供类比的结论是:设A、B为正定矩阵,则A+B正定.
由A、B对称,则A-B也对称,特别地当这两个矩阵相同时A-B就为零矩阵,显然结论不成立.反例如下:
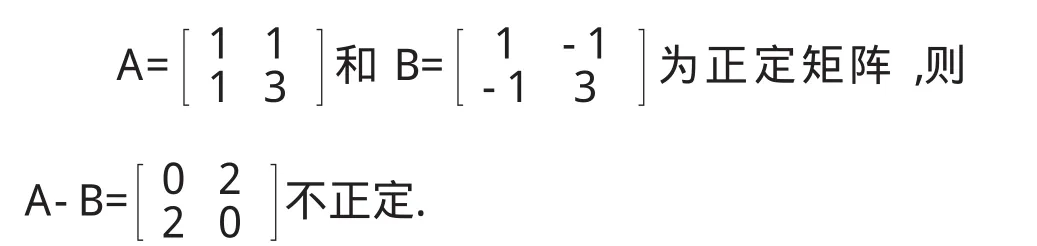
命题6设A、B为正交矩阵,则A+B也为正交矩阵.
分析:可类比的结论:设A、B为正交矩阵,则AB仍为正交矩阵.
要证(A+B)'(A+B)=I,左式展开为2I+B'A+A'B≠I,则反例:

结语
本文就高等代数中一些命题给出了运用类比思想构造反例.通过本文构造反例的过程,我们可引导学生在学习高等代数时积极主动地构造反例,从而加深对问题的理解,并养成独立思考、解决问题的习惯.
〔1〕张禾瑞.高等代数(第五版)[M].高等教育出版社,2007.
〔2〕黎伯堂,刘桂真.高等代数解题技巧与方法[M].山东科学技术出版社,2001.
〔3〕杨侠,孙自行.关于高等代数中命题的反例研究[J].阜阳师范学院学报,2010.27-4.
〔4〕徐言超.简析高等代数有关定理的条件反例[J].莱阳农学院学报,2004.
O15-4
A
1673-260X(2014)03-0009-02
