小波包和峭度在轴承早期故障分析中的应用

2014-07-21任学平庞震辛向志邢义通

轴承 2014年3期

任学平，庞震，辛向志，邢义通

(内蒙古科技大学机械工程学院，内蒙古包头 014010)

轴承的运行状态直接影响到整台机械设备的工作性能和运行效率。因此进行轴承故障检测诊断，进而对其预知维修，可以使机械设备运行可靠性大大提升。在实际应用中，对轴承结构与故障机理的了解，有助于利用各种现代分析手段进行有效诊断[1]。

目前，振动信号检测分析法广泛应用于轴承信号的故障诊断，首先采集工况下的信号，再对采集到的信号进行分析，以此诊断轴承故障类型。

小波包可以将小波分析没有细分的高频部分信号进一步分解，将信号分解的更加精细并使其分解到相邻的不同频率段上。使用小波包对轴承故障信号进行诊断分析时，通常采用小波包能量法选取节点系数并进行重构处理[2]。当信噪比较小时，一些含有噪声性质的细节系数会混入重构信号中，从而影响轴承故障诊断的结果。在此，结合小波包分解得到的细节系数并同时运用峭度准则原理，提出一种改进型的小波包包络方法，可在一定程度上提高故障诊断的精确度。

1 基本理论

1.1 小波包

小波包分析是小波分析的延伸，它可以对信号进行更为精细的分解与重构。小波分析可以将上一次分解得到的低频部分进行再分解，但不能对高频部分进行再分解，造成高频部分的分辨率很差。小波包分析对低、高频部分均可进行再分解，提高了高频段的分辨率，从而使整个信号的信息更为清晰。小波及小波包分解过程如图1所示。

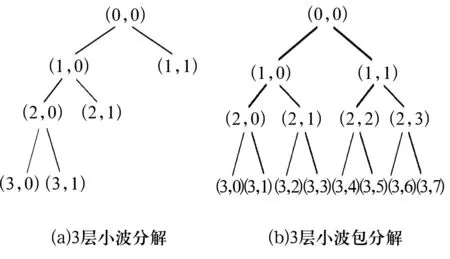
图1 小波和小波包分解过程

在小波包重构过程中，可根据需要选择全部或部分频段的信息进行重构，其他频段则归零处理，从而更加轻易辨别并提取重构频段故障信号。因此，只要区分出信号频段上的有用成分与噪声干扰成分，就可以得到滤除干扰噪声频段的重构信号。

1.2 峭度

轴承故障发生初期，引起的振动变化往往非常小，容易被其他信号掩盖。峭度是一个无量纲参数，与轴承的转速、尺寸及载荷等参数没有关系，但它对轴承造成的冲击信号格外敏感，尤其是表面损伤类故障，特别适合早期故障诊断。

峭度K是反映振动信号分布特性的数值统计量，是归一化的4阶中心矩，表示为

(1)

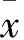
对于一组给定的离散振动信号数据，其离散化的峭度K为

(2)

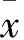
当轴承无故障运转时，受到各种不稳定、不确定因素的影响，振动信号的幅值分布往往接近于正态分布，峭度指标值K≈3；当轴承发生故障并不断地加深时，信号大幅值的概率密度不断增加，振动信号幅值分布发生偏离，正态曲线慢慢发生偏斜或分散，其峭度值也会随之不断地增大。峭度指标的绝对值从侧面反映了故障的严重程度，值越大，说明轴承越偏离正常运行状态，信号中故障信息成分所占的比重越多，产生的故障越严重[3-4]。当K>8时，很可能发生严重的故障。

1.3 轴承故障信号分析具体步骤

结合小波包与峭度对轴承故障信号诊断的流程如图2所示，主要有以下步骤：

(1)确定信号小波包基与层数，并分解信号；

(2)对分解后小波包节点系数进行阈值量化；

(3)求最底层各节点系数的峭度值，根据峭度原则，去除含噪信号的细节系数；

(4)提取故障信息的系数并进行小波包重构；

(5)包络谱分析[5-6]，提取故障信息。

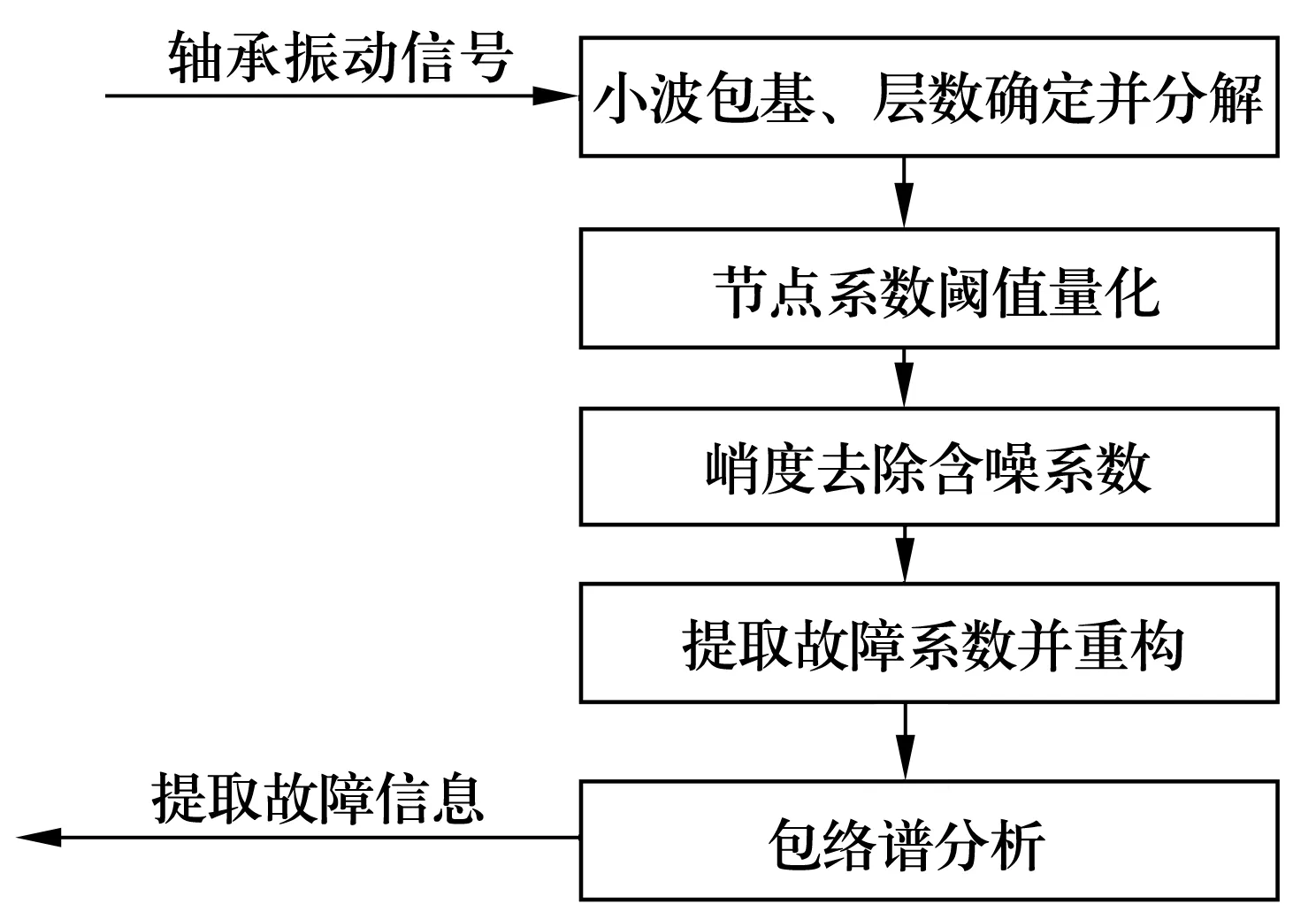
图2 小波包与峭度分析流程图

2 仿真信号分析

为验证小波包降噪的良好效果及峭度对故障信号精确度的提高，对具有实际故障特征的仿真信号y(t)=0.1sin(2π×100t)+randn(t)进行小波包降噪。y(t)是信噪比很低的故障仿真信号，主要成分为噪声，依据峭度准则，小波包降噪后各节点系数的峭度值应在3附近和8以下，小波包降噪后各节点系数的峭度值见表1，选取(3，0)，(3，3)，(3，6)和(3，7)作为重构信号，重构后的信号为y″(t)，如图3所示。

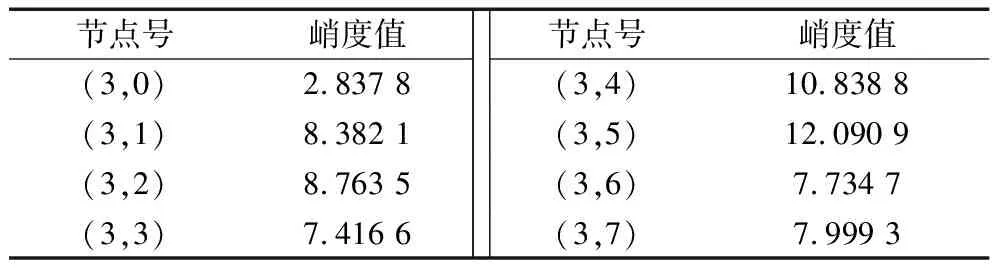
表1 各系数的峭度值

对比图3中的3个信号，小波包降噪信号y′(t)降噪效果很好，而通过峭度得到的信号y″(t)略去了更多噪声干扰信号。对y″(t)进行频谱分析处理后的结果如图4所示，从图中可以轻易找到频率100 Hz。

图3 仿真信号

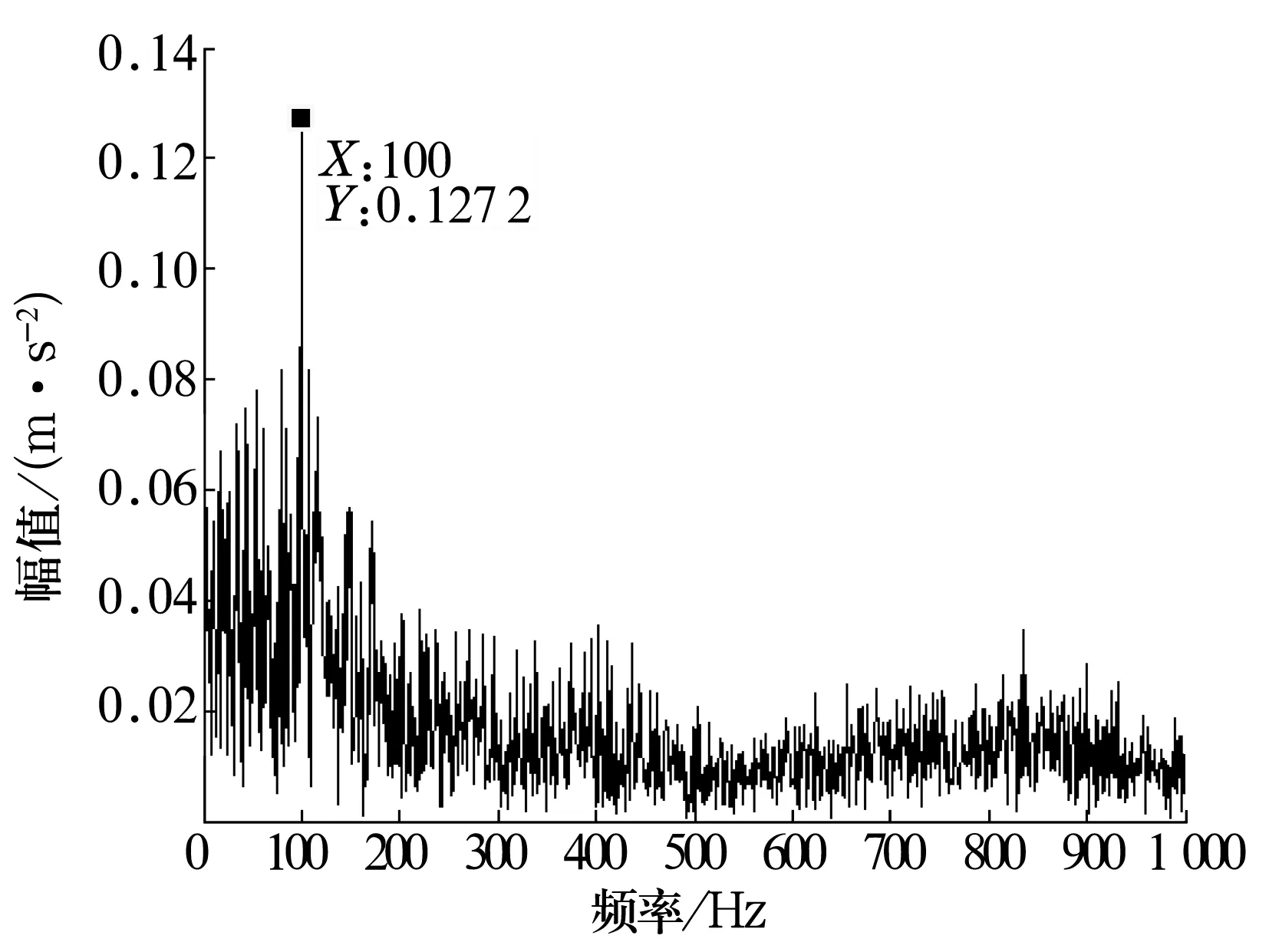
图4 重构信号的频谱

3 试验分析

3.1 试验结构及故障信号

为验证上述方法的效果，采用ZonicBook测试系统获取轴承故障振动信号，并利用小波包与峭度准则对轴承振动信号提取故障特征。试验台结构如图5所示，主要由电动机、转子、加载器及轴承组成。试验轴承为N205EM圆柱滚子轴承，外圈故障如图6所示，为宽0.1 mm，深0.2 mm平行于轴承轴线的微小沟槽，轴承内圈完整无缺。

图5 试验平台

图6 轴承外圈故障

轴承内径25 mm，外径52 mm，宽度15 mm，滚子直径7.5 mm，滚子组节圆直径39 mm，滚子个数为12，接触角为0°。试验中外圈固定，内圈旋转，使用采样频率为10 240 Hz的数据采集卡与加速度传感器对1 350 r/min转速下的轴承进行数据分析，轴承各部件故障特征频率见表2。

表2 轴承各部件故障频率 Hz

当轴承外圈发生局部故障时，由于故障位置不变，承载大小不发生变化，冲击振动的振幅大致相同，所以故障信号为高频固有振动信号与外圈故障特征频率信号调制而成[7]，包络谱应当包含外圈故障的特征频率。外圈故障信号的时域波形及其频谱如图 7 所示，由于工频振动幅值远大于轴承故障所引起的高频振动，所以无法直接从频谱上提取故障信息。

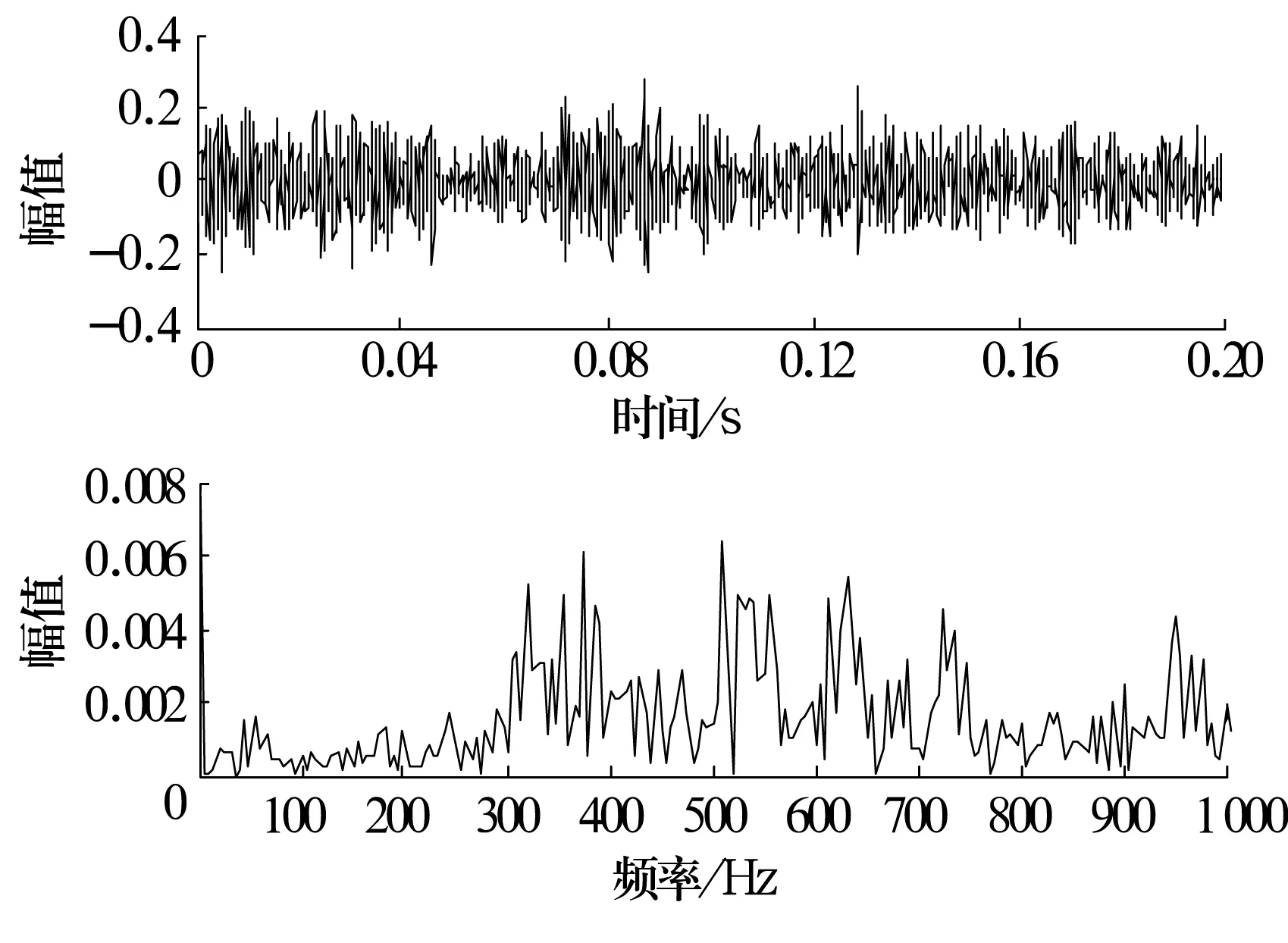
图7 轴承外圈故障信号

3.2 小波包能量法

小波包能量法首先对振动信号进行小波包分解，然后使用各细节系数的能量与原振动信号的能量的比值作为选取重构细节的标准，对原振动信号进行3层小波包分解，得到信号细节系数的能量与原信号的能量比值见表3。

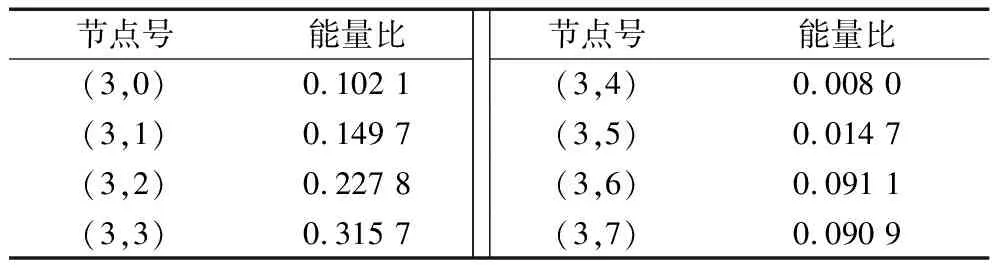
表3 各系数与故障信号间的能量比值

可以看出(3，0)，(3，1)，(3，2)和(3，3)这4个细节信号的能量与原振动信号的比值比较大，选择这4个细节系数进行重构，并对重构信号进行Hilbert解调，结果如图8所示。从图中可以看出故障频率100 Hz不明显，信号中存在的噪声信号并没有完全剔除。

图8 小波包能量法的包络解调谱

3.3 小波包与峭度法

先对原振动信号进行3层小波包分解，再对各小波包节点系数进行阈值去噪，去噪后各系数的峭度值见表4。

表4 去噪后各系数的峭度值

由于轴承设置为初期故障，峭度值应大于3小于8，由表4可以看出依然存在导致峭度值超过8的(3，1)，去除该分量后对(3，0)，(3，2)和(3，3)进行小波包重构及Hilbert包络谱分析，结果如图9所示。

对比图8和图9可以看出，2种方法得到的解调频谱信号最大值都出现在110 Hz, 故障频率误差范围一般在3 Hz以内，外圈故障频率109.35 Hz与其接近, 可以判定与外圈故障特征频率理论计算值基本一致。但小波包与峭度方法剔除了具有噪声信号性质的细节系数(3，1)，减少了噪声的引入，从而使解调后信号频谱中的外圈故障频率明显突出，噪声干扰频率减少很多，可以更准确的诊断轴承故障情况。