基于ABAQUS的列车轴箱轴承动力学分析

郝烨江，李强，郑静

(北京交通大学 机械与电子控制工程学院，北京 100044)

符号说明

B——轴承宽度

C0——轴承额定静载荷

d——轴承内径

D——轴承外径

Dpw——滚子组节圆直径

Fa——轴向载荷

Fap——轴承的轴向承载能力

Fc——滚子离心力

FL——转臂效应载荷

Fr——径向载荷

Ft——牵引制动载荷

g——重力加速度

Gr——径向游隙

Hz——轴承承载区宽度

I——节点内力

k1，k2——载荷系数

K——载荷-位移系数

Lt——滚子有效承载长度

Lz——转臂长度

ma——轴重

ms——簧下质量

M——节点质量矩阵

n——轴承转速

ni——内圈转速

nc——保持架转速

P——系统外力

Qi——第i个滚子的径向载荷

ü——节点加速度矩阵

Z——滚子数

α——接触角

γ——计算参数

Δt——时间增量

δi——第i个滚子的径向位移

δr——沿径向力方向产生的总位移

φi——第i个滚子的方位角

列车轴箱轴承是确保列车运行品质和安全性的关键技术部件，通常使用双列圆锥滚子轴承或双列圆柱滚子轴承。由于结构及使用工况的特点，轴承在运行周期内承受的载荷十分复杂，受多方面因素的影响。轴承失效形式多种多样，但大多数集中在表面接触疲劳损伤和次表面缺陷疲劳扩展方面。对于轴承，除保证良好工作条件并定期检修外，针对性地研究其在不同工况下的动力学特性对于改进结构、提高寿命意义重大。文中以BC2-0375型列车轴箱轴承为对象建立分析模型，按照实际载荷工况加载边界条件，利用有限元方法对其动力学特性进行求解分析[1-3]。

1 轴箱轴承径向载荷

轴箱轴承承载状况极为复杂，受到轮轴、转臂等多方面因素的影响(图1)，很难给出完全符合实际条件的载荷计算公式，通常采用的径向力简化计算式为

Fr=(mag-msg)/2+Ft+FL。

(1)

图1 轴箱轴承受力示意图

簧下质量根据列车型号基本固定不变；轴重取列车空载状态下的质量；牵引制动载荷通过牵引功率和制动加速度求得；转臂效应载荷由转臂受到轴向载荷导致的轴承偏转产生(图2)，即

FL=FaLz/Hz。

(2)

图2 转臂效应载荷计算示意图

参考轴承几何尺寸并根据实际载荷状况和润滑条件的影响对参数加以修正，得到径向力的最终计算式为

Fr={-Fap+104k1C0/[n(d+D)]}/k2。

(3)

BC2-0375型列车轴箱轴承为圆柱滚子轴承，其简化模型的几何参数为：d=130 mm,D=240 mm,B=80 mm; 按照n=900 r/min，C0=1 560 kN，代入相应的载荷系数，由(3)式得到稳定运行情况下等效的径向载荷为25 kN，由此得到计算模型加载的载荷边界条件[4-6]。

2 工作状态下轴承内部载荷分布

在径向力与转速恒定的情况下，轴承会形成稳定的承载区间，如图3所示。通常转速不是很高的时候，滚子的离心力、摩擦力和力矩对载荷分布不会产生特别明显的影响。数值计算的基本思路是建立滚子与滚道间的载荷-位移关系，通过迭代求解非线性方程组获得位移分布，从而最终获得轴承内部的载荷分布。

图3 轴承内部承载区示意图

假定轴箱轴承径向游隙为零，根据几何尺寸可得计算参数γ为

γ=Dcosα/Dpw=0.144 385，

(4)

保持架和内圈转速间的运动关系为

nc=0.5ni(1-γ)=0.427 81ni，

(5)

绕轴承轴线以nm转速运动的钢制滚子的离心力为

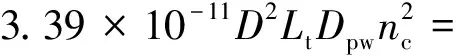
(6)

在低速条件下，离心力对于滚子与滚道间的接触载荷贡献很小；但在高速时离心力的效应显著。由于所计算轴承的转速集中在1 200 r/min以内，产生的离心力效应基本可以忽略。

在轴承的径向载荷作用方向，根据力的平衡条件可得

(7)

根据载荷-位移系数换算得到

(8)

轴承工作状态下内、外滚道与滚子间的位移关系为

(9)

联立 (8)～(9)式，建立由18个方程组成的非线性方程组，通过Newton-Rampson法对其进行迭代求解，得到滚子与外圈滚道的位移分布，再利用载荷位移系数进行修正就可得到轴承的内部载荷分布。将上述求解过程利用MATLAB程序语言进行描述，分别对420和900 r/min转速下的轴承内部载荷分布进行数值计算，得到的结果如图4所示。

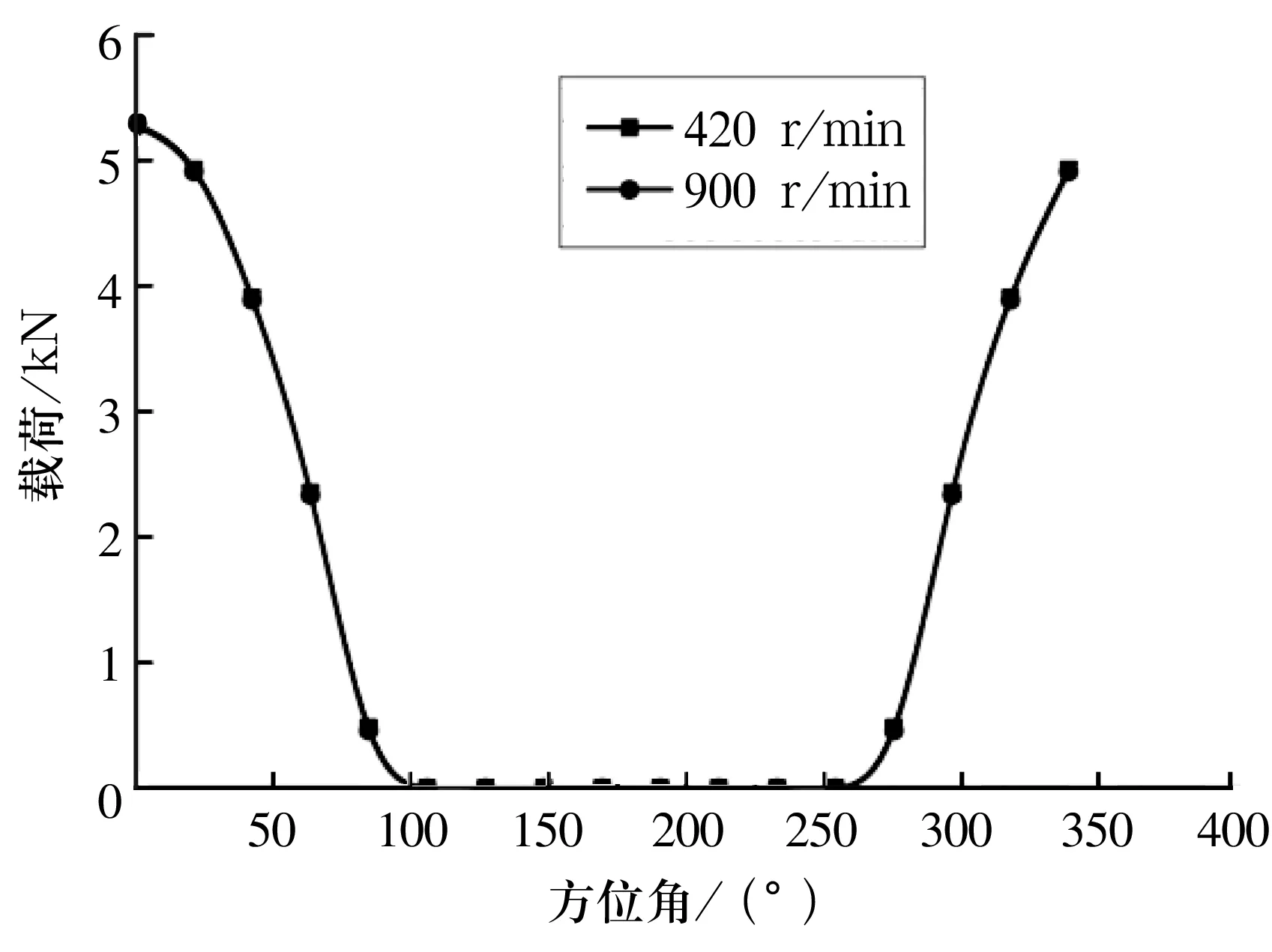
图4 轴承内部载荷分布

由图4可知，最大载荷出现在方位角为0的位置，载荷随着方位角的增大而减小，直至承载区之外滚子不受载荷作用，承载区域约为168°。中低转速区间，转速的提升对于轴承外圈所受载荷的大小及分布影响并不显著，承载区域没有发生大的变化。在忽略滚子滚动摩擦效应的情形下，位于承载区各位置滚子的接触应力可以按Hertz接触理论计算得出。方位角为0处的内圈的接触应力为625.545 MPa，接触区域半宽为0.126 8 mm；外圈接触应力为542.174 2 MPa，接触区域半宽为0.142 9 mm，这些结果是进行有限元离散求解的参考基础[7-9]。

3 基于ABAQUS的显式动力学计算

ABAQUS-explicit是一种高效的求解复杂非线性问题的数值计算工具。接触问题是一个典型的复杂非线性问题，本构关系即使是处于线性区，接触区域的局部效应也会使得接触应力通常到达塑性区，尤其对于轴承来说，接触应力达到1 380 MPa以上的情况并不少见；再加之其所处的边界条件的非线性，无法事先知道应力的分布，接触应力与接触区域互相影响，呈现出高度的非线性特质。对于静态基本几何外形的非共形接触，已经由Hertz理论得到了较为精确的解答。

轴承的动态接触问题较之经典接触对之间的接触要复杂许多，轴承零件之间的接触关系时刻发生变化，且受到内部载荷分布、润滑效应以及材料等多方面因素的影响。使用隐式求解方法进行解答可以平稳地建立接触关系，减小冲击效应产生的应力波的影响，但对于接触对建立条件的要求复杂很多，而显式计算中的通用接触模式(general contact)可以很方便地建立这种接触关系，且不存在收敛问题，适合于求解内部结构关系多变且存在复杂相互接触作用的瞬时动态响应问题。但是ABAQUS-explicit对于求解轴承接触问题的缺点在于初始力边界条件施加时会产生应力波干扰，这种冲击的效应需要加大载荷步长度来进行削弱，计算量也随之上升[10]。

3.1 ABAQUS-explicit求解器算法描述

ABAQUS-explicit应用中心差分算法对运动方程进行显式的时间积分，由一个增量步的动力学条件计算下一个增量步的动力学条件。在增量步开始时，求解动力学平衡方程

Mü=P-I，

(10)

在当前增量步开始时，计算加速度

ü|(t)=M-1·(P-I)|(t)。

(11)

显式算法并不需要同时求解联立方程组，任何节点的加速度完全取决于节点质量和作用在节点上的合力。对加速度在时间上进行积分采用的是中心差分法，在计算速度变化时假定加速度为常数,将速度的变化值加上前一个增量步(increment)中间时刻的速度来确定当前增量步中间时刻的速度，即

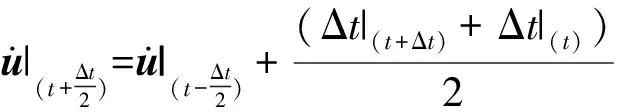
(12)

再利用速度对时间的积分与增量步初始位移求和,即可得到增量步末的位移

(13)

得到节点位移后，即可通过应变速率和本构关系获得节点的应力矩阵[11]。

3.2 有限元模型的建立

轴承运行过程中，滚子与内、外滚道及保持架之间存在着复杂的运动和接触关系，且由于保持架和滚子之间的碰撞以及内、外滚道之间的阻尼效应，往往内圈和保持架转动并不同步，这也就影响到了滚子承受循环载荷的频率。为了尽量真实模拟轴承零件的动力学关系，将滚子，内、外滚道以及保持架均按照弹性体进行建模。

取单列轴承为对象，根据几何参数利用ABAQUS集成的modeling模块完成几何模型的建立，忽略倒角、注油孔以及一些边缘细节。径向游隙为0，保持架与滚子间的间隙为0.5 mm。忽略微小区域塑性应变，材料选定在线弹性范围内。单元类型选择减缩积分单元C3D8R，扫掠形成网格。需要注意的是由于接触区域附近的离散化质量直接决定了计算精度，为了得到准确的接触应力，根据大量接触问题的有限元计算结果，取接触区域的单元尺寸为接触区域半宽的一半，如果是椭圆形接触区域，则需小于短半轴长度。离散后的有限元模型如图5a所示。

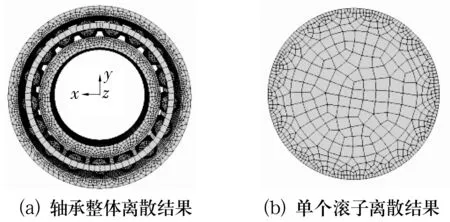
图5 轴承有限元离散结构

滚动体接触区域附近网格的质量也会对应力分布产生很大的影响，故将滚子分为2个环形区域，外环形区域加密网格，保证均匀度;内环形区域疏化,减小计算规模，如图5b所示，单元数目为138 939，节点数目为176 517。

内、外滚道以及滚子弹性模量为207 GPa，密度为7.8×10-6kg/mm3，泊松比为0.3。保持架弹性模量为120 GPa，密度为8.5×10-6kg/mm3，泊松比为0.34。

利用显式计算的通用接触建立轴承接触模型，在运算过程中，ABAQUS将所有的零件生成一个实体模型，通过设置自接触来判断接触区域，从而实现复杂接触模型的建立。法向接触属性采用硬接触，接触刚度和罚函数系数将根据实际接触区域的变形自动调整。切向接触属性中的摩擦模型采用库仑摩擦，内、外圈滚道与滚子之间静摩擦因数给定为0.1,动摩擦因数给定为0.05，衰减系数取0.01；滚子与保持架之间摩擦因数在中低转速区间对结果影响不大，简化后给定为0.002。

边界条件：内圈节点耦合在圆心处,在初始分析步中仅放开沿y轴(垂向)的径向自由度；保持架耦合在圆心处，只释放绕轴线的旋转自由度；外圈始终施加全约束；分析全程设定5个载荷步，step1至step5：step1(0.01 s)中对滚子施加重力加速度，使接触可以稳定的建立；step2(0.02 s)中在内圈耦合点施加垂向载荷25 000 N；step3(0.1 s)放开内圈耦合点的绕轴线的旋转自由度，施加200 r/min转速;step4(0.1 s)在step3的基础上继续增加转速达到420 r/min;step5(0.1 s)继续将转速增加到900 r/min。

所有的载荷施加形式均选定光滑曲线(smooth step)加载，尽量减小系统应力波的震荡。

3.3 计算结果分析

显式计算的速率与节点质量的开方值成反比，网格越精细，计算所需的时间增量步越多，计算时间越长，复杂的接触模型计算消耗的时间较长，可以选择相应的质量放大系数，在保持精度的条件下实现轴承接触的动力学仿真。

(1)不同转速等级下轴承内部的载荷分布情况与Newton-Rampson算法得到的载荷分布结果基本一致，且在加速过程中承载区也较为稳定，在中低速时滚子与滚道接触产生的等效应力场水平并没发生很大的变化，基本维持在1 000 MPa以内，且最大值出现在滚子边缘处，这是由边缘压膜效应产生的应力集中现象造成的，如图6所示。各个载荷步最终的应力分布如图7所示。当转速提升到900 r/min,平均应力水平增大，某些瞬时时刻的最大应力出现在承载区的滚子与保持架之间(由碰撞所产生)。这说明轴承持续加速过渡阶段保持架起到了重要的作用，其强度决定了加速运转的可靠性与安全性。

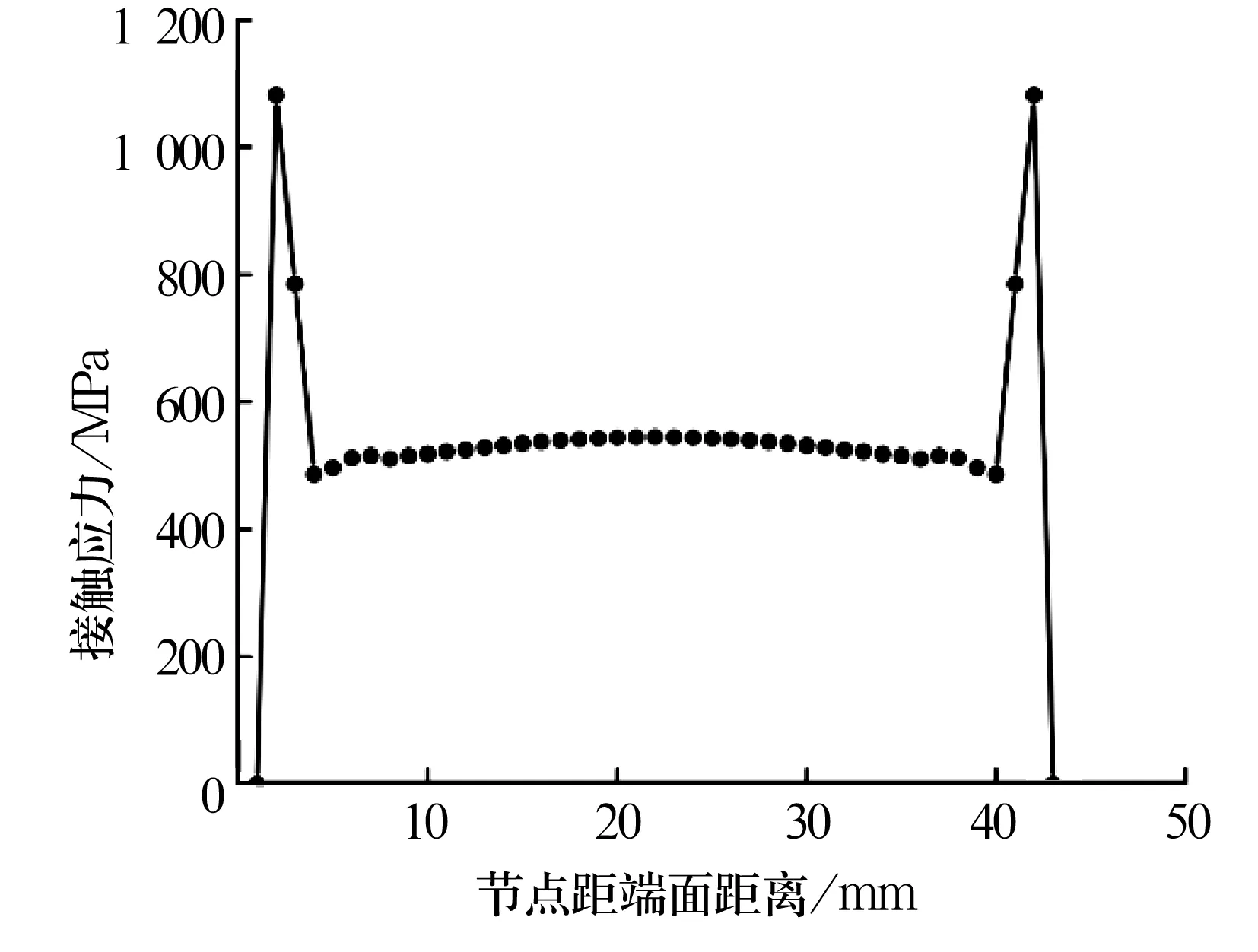
图6 滚子接触应力分布

输出外圈内表面与对称中面交线中点即6 027号节点(图8)在不同转速下的等效应力曲线，如图9所示。

由图9可知，随着转速升高，单位时间内的应力峰值数目增多，受载频率变大，但峰值并未显著增大，说明中低转速产生的离心力作用并不显著。

图8 第6 027号节点位置

图9 第6 027号节点在不同转速下的等效应力曲线

step2中径向力加载稳定后，外圈与方位角为0的滚子所构成的接触对中，外圈接触区域中心平均接触应力为480.309 MPa，滚动体接触区域中心平均接触应力为645 MPa；内圈与方位角为0的滚子构成的接触对中，内圈接触区域中心平均接触应力为630.702 MPa，滚动体接触区域中心平均接触应力为723.5 MPa(图10)。理论上同一个接触对，接触区域的应力对于两接触体应相同，产生的差值由离散化计算导致，网格的密度与均匀程度决定了接触应力计算的准确度，内、外圈接触区域网格的大小为2 mm，约为滚子的10倍，导致滚子接触应力偏大，滚道接触应力偏小，将对应节点的接触应力取平均值作为接触应力数值计算的结果。则滚子与内、外圈间的接触应力分别为677.101，562.65 MPa，与理论计算值相差分别为7%，3%。

(2)轴承即使是理想几何形状，也会由于各个滚子角位置的不断变化而产生内、外圈的周期性相对运动，其振动频率等于保持架运动速度与滚子数之积，即滚子通过外圈滚道的频率，类似于弹簧的振动。轴承的振动频率往往影响着转向架系统尤其是轴向轮对及牵引系统的振动频率，称之为可变弹性柔度。采集step1至step5的内圈耦合点的垂向位移，如图11所示。

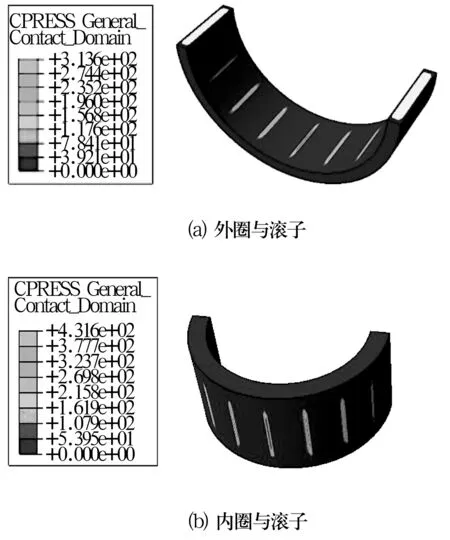
图10 轴承接触应力分布

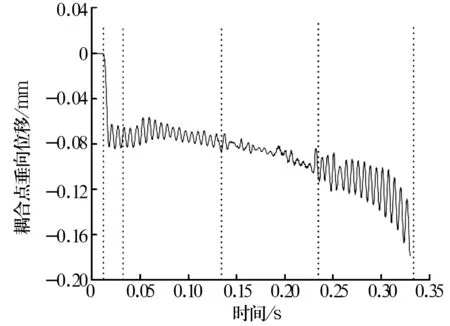
图11 内圈耦合点的垂向位移时间历程

由图11可知，在5个载荷步的时间历程中，step1重力加载时耦合点并未出现显著的垂向位移；step2径向力加载时出现较大的垂向位移，末端有一段时间的应力波激扰衰减过程；step3转速施加后，位移呈现周期性变化，转速为200 r/min时，轴承的可变弹性柔度频率为120.48 Hz，与理论计算得到的频率(145.758 Hz)基本吻合。且随着转速的提高，内圈耦合点位移变化周期逐渐减小，但是趋势并不明显，原因在于使用了平滑曲线加载，在载荷步末端才达到目标转速，且计算时间较短，并没有显示出较为明显的频率变化。随着转速提高，由于离心力作用加大以及内圈的变形导致的垂向位移波动振幅变大，趋势越发清晰[12-13]。这种高频的振动需要在信号采集结果处理时滤掉，否则会影响分析精度。

4 结束语

(1)根据列车轴箱轴承结构特点和受力分析求解了单列轴承承受的径向载荷。

(2)采用Newton-Rampson法，利用MATLAB求解了转动状态下轴承内部载荷的分布情况，并根据Hertz接触理论求解了最大载荷作用接触区域的接触应力，将其作为有限元计算的参考。

(3)建立了有限元离散模型，加载计算得到的载荷和相应的转速工况，研究轴承的动力学特性，获得了不同转速条件下轴承内部应力场与位移场，得到的等效应力分布与实际工况和理论解相符合，实现了轴箱轴承的显式动力学模拟；并进行了相关动力学特性分析，以此为基础，可以对轴箱轴承各种运行失效状态进行模拟仿真，找出各种不同失效形式下振动和应力分布的特点，为故障诊断提供可靠的参考依据，并可借此提出相应的轴承在线检测方法。