圆柱滚子轴承滚子打滑机理研究

刘红彬，张帅，邢国玺，张磊，薛玉君

(河南科技大学 机电工程学院，河南 洛阳 471003)

轴承在转动过程中，由于内圈转速和载荷等多种因素影响，滚动体会出现不同程度的打滑现象。打滑发生后轴承内部摩擦和发热加剧，打滑率过大会导致轴承迅速烧伤损坏[1]。因此，对轴承进行打滑失效分析显得尤为重要。

多年来，国内、外许多学者通过对轴承进行拟动力学和有限元动力学仿真研究来揭示滚动体打滑机理。随着计算机水平的高速发展，有限元成为解决轴承静力学和动力学问题的有效方法，从滚动体载荷分布到滚动体与滚道的摩擦学特性研究都为滚动体打滑机理研究奠定了理论基础。文献[2]运用有限元方法对滚子进行静力学分析，获得滚子与滚道的接触应力分布规律。文献[3]采用拟动力学法分析高速球轴承载荷分布的数学模型。文献[4]采用Newton-Raphson法分析圆柱滚子中介轴承的数学模型，得出滚子打滑率与径向载荷间的关系。文献[5]分析轴承在不同径向载荷下和不同位置角处滚子自转速度变化规律。文献[6]采用拟静力学和拟动力学相结合的方法研究高速球轴承打滑的临界载荷。文献[7]运用轴承拟动力学方程组，并耦合弹流润滑理论，对高速轴承打滑失效分析过程进行较为深入的研究。此外，文献[8]还利用拟动力学法计算分析考虑涡动工况的高速轴承打滑失效机理。文献[9]通过建立6自由度动力学模型研究圆柱滚子转速稳定性对打滑发生的影响。文献[10]通过试验研究温度、滚子个数和载荷对滚子打滑的影响规律。

上述有关轴承动力学分析和滚动体打滑率的研究未将轴承各组件柔性化处理，轴承内部各组件间的接触计算采用弹性接触的方法处理，但均未考虑接触引起的各组件变形。利用有限元理论对轴承进行柔性化处理，可更为准确地反映轴承各组件间的接触力变化。文献[11]在ANSYS/LS-DYNA中对深沟球轴承进行仿真分析，得出载荷和转速对轴承等效应力的影响和故障轴承的振动特性比较。文献[12]基于塑性材料模型对圆柱滚子轴承进行显式动力学计算，分析轴承变形对轴承运转的影响规律。文献[13]通过对保持架的柔性化处理计算分析保持架的平稳特性和打滑率。滚子与滚道间柔性接触的建立可更为准确地模拟滚子与滚道间的动力学关系。因此，以圆柱滚子轴承为例，在ABAQUS/Explicit中建立轴承的全柔性模型，综合考虑内圈转速、径向载荷和过盈配合产生的压力等因素，运用显式动力学方法对轴承进行动力学仿真，通过提取轴承动力学计算结果中滚子中心节点速度变化历程，获得滚子相对滚道理想纯滚动的打滑率，并分析其影响因素和规律。

1 显式算法说明和弹性波的波动方程

1.1 显式动力学理论

轴承动力学有限元分析数学建模中，系统的动力学方程为

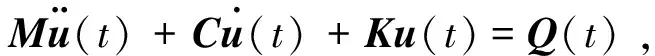
(1)

(2)

(3)

(4)

ABAQUS/Explicit 计算方法中采用中心差分法对运动方程进行显式时间积分。计算中采用上一增量步的动力学结果作为下一增量步的动力学计算的初始条件。每个增量步开始时节点的平衡方程根据(2)式得到，节点的加速度取决于质量矩阵和节点所受的合力；速度根据(3)式得到，此增量步内的加速度可根据前后增量步的速度变化值确定，前一增量步中点的速度加上速度变化量确定当前增量步中点的速度；位移由速度对时间的积分和增量步开始时的位移确定，根据(4)式可得节点在增量步的位移。

只有足够小的增量步才能保证增量步内的加速度近似为常数和积分结果的准确性，ABAQUS可估算出最小稳定时间增量步积分步长，使之小于中心差分算子的稳定极限，确保中心差分法的数值稳定。

1.2 连续体中的应力波动计算

轴承在动态条件下，滚子由非承载区进入承载区，再到滚子受载最大位置，时间历程非常短。滚子表面质点先受到内、外圈的柔性接触载荷，使其偏离初始平衡位置。滚子部分质点与相邻滚道质点发生相对运动，接触部位质点间会产生接触应力和摩擦力，二者的相互作用力使相邻的质点产生位移，从而使转动部件产生弹性波。柔性动力学有限元计算分析中，质点不像静力学情况下处于静力平衡状态，而是处于随时间迅速变化的动态过程，此弹性波在轴承中传递形成应力波，因此建立柔性体中的弹性波的波动方程为

(5)

式中：λ和μ为Lame常数；ρ为材料密度；t为时间；x1，x2和x3分别为空间坐标轴的3个方向；ε11=∂u1/∂x1，ε22=∂u2/∂x2和ε33=∂u3/∂x3分别为增量步内3个方向上的主应变；u1，u2和u3分别为微元在一个增量步内3个方向的位移变化。通过建立波动方程可更为准确地获得轴承在工作过程中应力波动的传递过程。

2 动力学计算分析

2.1 圆柱滚子轴承几何参数

以NU1020圆柱滚子轴承为例建立动力学分析模型，轴承几何参数见表1。建模未考虑轴承套圈的安装圆角和加工工艺倒角。为了准确模拟滚子与滚道的柔性接触，滚子的圆角在建模中未予省略。

表1 轴承几何参数

2.2 有限元模型的基本假设

(1)材料模型假设：忽略材料因热处理或混有杂质表现出的不同力学性能，宏观上把物体视为由连续不断的质点构成，视模型为质点的连续集合。

(2)线弹性假设：此模型中材料为线弹性，即应力与应变间的关系严格遵循Hooke定律。

(3)使用修正的Kragelskii函数代替油膜对摩擦因数的影响：通过接触属性的设置代替轴承中油膜的存在和复杂的接触作用力，这样能简化模型，提高计算速度[14]。

f=(-0.1+22.28s)e-181.46s+0.1，

(6)

式中：f为摩擦因数；s为滑滚比。

(4)恒温假设：忽略周围环境对轴承产生的阻力和温度的变化对轴承动态性能的影响。

2.3 有限元模型建立

(1)材料赋值：建立全柔性模型来仿真轴承工作过程中的动态状况，内外圈、滚子和保持架均采用柔性材料GCr15钢，弹性模量为207 GPa，泊松比为0.3。

(2)单元的选择：根据内、外圈和保持架形状规则，选择C3D8R单元类型，其单元在每个积分方向少使用一个积分点，可缓解单元过硬现象。滚子采用C3D10M单元类型对沙漏进行控制。节点共计269 012个，单元85 347个。其中线性六面体单元(C3D8R)35 992个，二次六面体单元(C3D10M)149 355个。轴承有限元模型如图1所示。

图1 轴承有限元模型

(3)柔性接触设定：为仿真接触表面间切向和法向作用力，在滚子表面和内滚道、外滚道、保持架兜孔面间添加接触对和接触属性。接触对采用面与面的接触类型，接触控制方法选取动力学接触控制。法向接触为防止接触穿透而采取Hard设置，切向摩擦因数采取修正的Kragelskii函数。

(4)径向加载：在内圈的内径面和内圈的几何中心点建立位移耦合，同样在保持架的侧面和保持架的几何中心建立耦合。通过对内圈耦合加载实现对内圈径向加载。

(5)载荷边界条件：轴承边界条件如图2所示，对外圈外径面施加固定约束。实际工程中内圈与轴系相连，提供旋转动力，故对内圈轴向移动施加约束，释放绕轴线旋转的自由度。对保持架施加轴向约束，以防止仿真过程中滚子和保持架的轴向窜动。

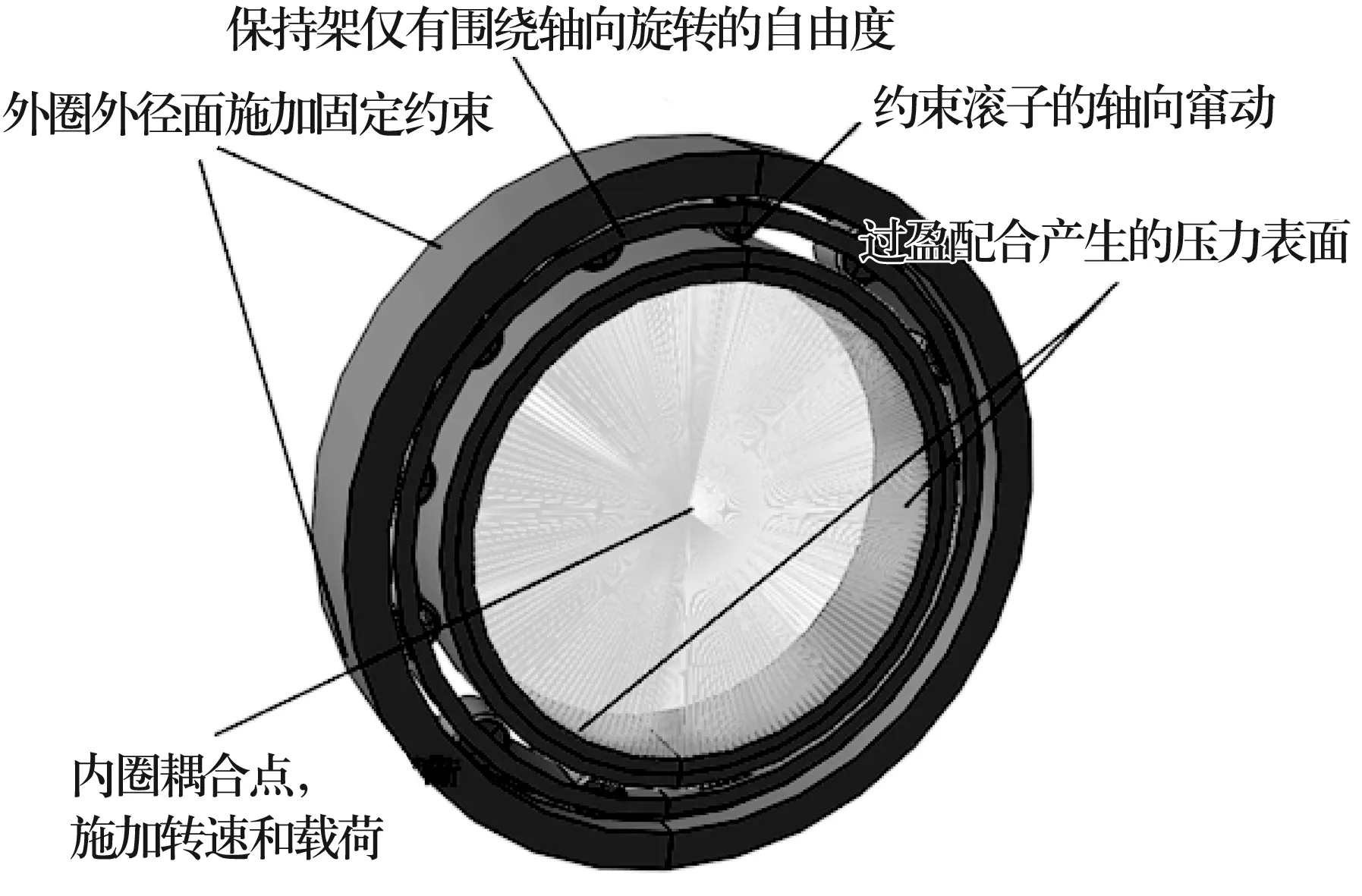
图2 轴承边界条件

(6)分析步的设定：第1个分析步中施加径向载荷，时长取0.5 s，以保证径向加载引起的响应得以稳定；第2个分析步中施加内圈的旋转，时长取20 s，以分析滚子在轴承旋转过程中的打滑。

(7)局部质量放大：在显式算法中稳定极限由模型单元中最小的单元决定，最小稳定时间增量方程为

(7)

式中：Le为特征单元长度；cd为材料的膨胀波速；E为材料的弹性模量；ν为材料的泊松比。

合理的质量放大能有效利用计算资源。未倒角的滚子在分析时出现应力集中，滚子边缘的奇异网格导致计算失败。对滚子进行倒角能有效减小应力集中，但倒角带来的细小网格会减小模型的最小时间增量，故对滚子和保持架倒角部位的单元及其他不规则单元进行质量放大，在分析打滑率不失真的同时节省计算资源。

3 计算结果及分析

3.1 运动状态分析

由于NU1020圆柱滚子轴承的内圈参考额定转速为4 150 r/min，故选取2 075，2 490，2 905，3 320 r/min为仿真转速。该轴承的基本额定动载荷为116 kN，故选取基本额定动载荷的2%，3%，4%，5%，即2.32，3.48，4.64，5.80 kN为径向载荷。过盈配合产生的压力分别选取0，50，100，150，200 MPa进行等效代换。

内圈转速为2 075 r/min，径向载荷为2.32 kN，无过盈配合时，轴承工作过程中各组件的速度云图如图3所示。

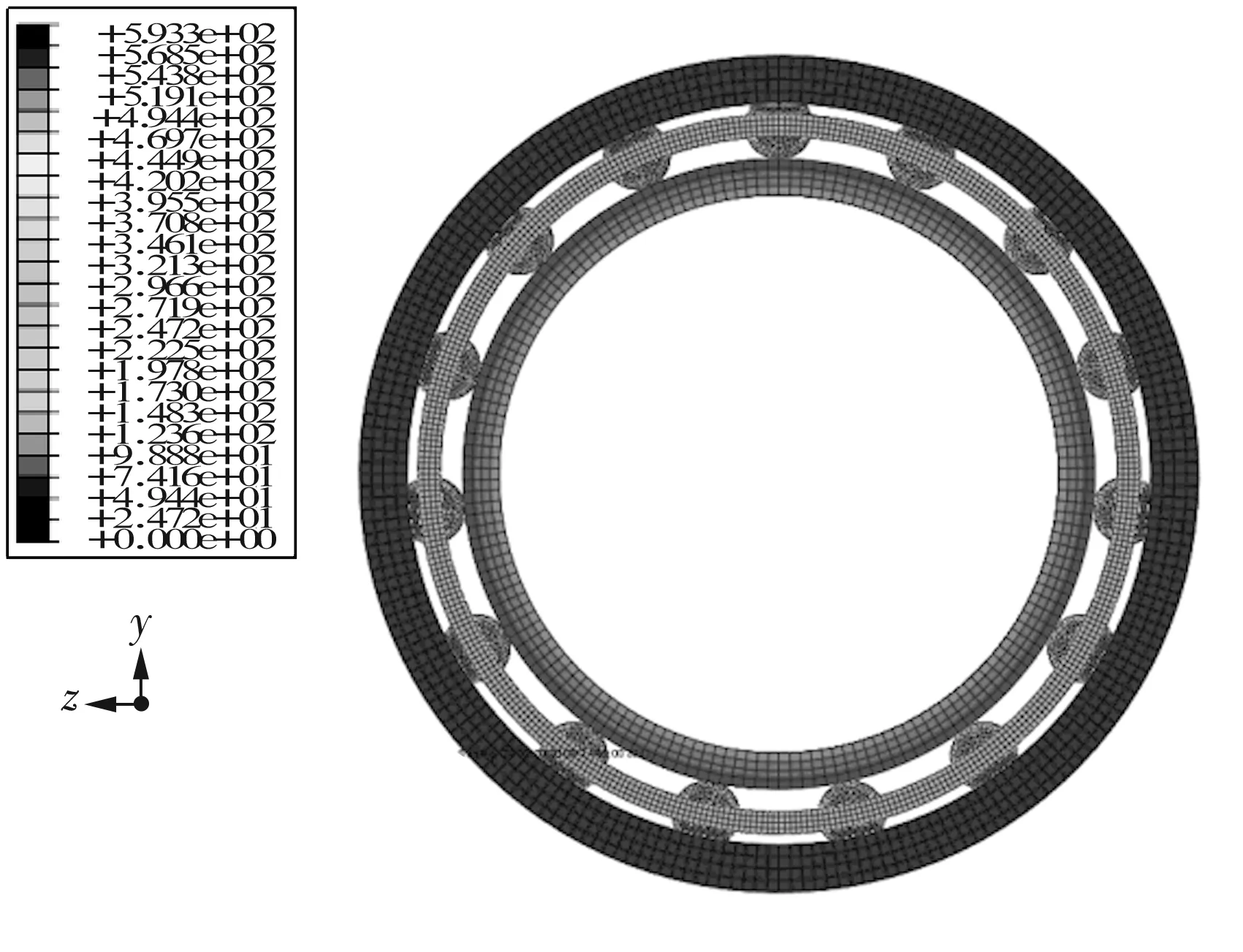
图3 轴承工作过程中各组件的速度云图

由图3可知，内圈旋转带动滚子和保持架的旋转，且各组件节点拥有不同的速度。外圈处于固定状态时，速度为0，轴承工作过程中内、外圈和滚子的速度云图如图4所示，内圈速度高于保持架速度。滚子中各节点的运动属于平面运动。各节点的速度规律符合平面运动规律。此外，在运转过程中，滚子和外圈接触处的速度低于和内圈接触处的速度，且滚子的速度瞬心轴和滚子与外圈接触线重合。

图4 轴承工作过程中内、外圈和滚子的速度云图

有限元分析需用网格对轴承进行离散化，离散化后的各个节点拥有不同的动力学信息。为了研究分析滚子打滑机理，提取节点的速度随时间的变化历程。提取节点的位置如图5所示。内圈内径耦合面和滚道的速度如图6所示。内圈内径耦合面的设定速度即为轴承内圈运动输入，设定内圈内径节点速度在2 s内从零线性增至规定线速度。内圈滚道节点理论速度为内圈内径和滚道的转动半径的乘积。内圈滚道节点实际速度是根据动力学仿真计算结果提取得到的节点实际线速度。从内圈滚道节点实际速度和理论速度对比可知：轴承启动运转时，内圈滚道上的节点和滚子发生接触和摩擦，根据显式动力学理论和柔性连续体的应力波动计算，随内圈转动，滚道表面节点速度与滚道理论速度存在一定差别，其波幅随时间的增加而增加，且最终趋于稳定。

图5 提取节点的位置

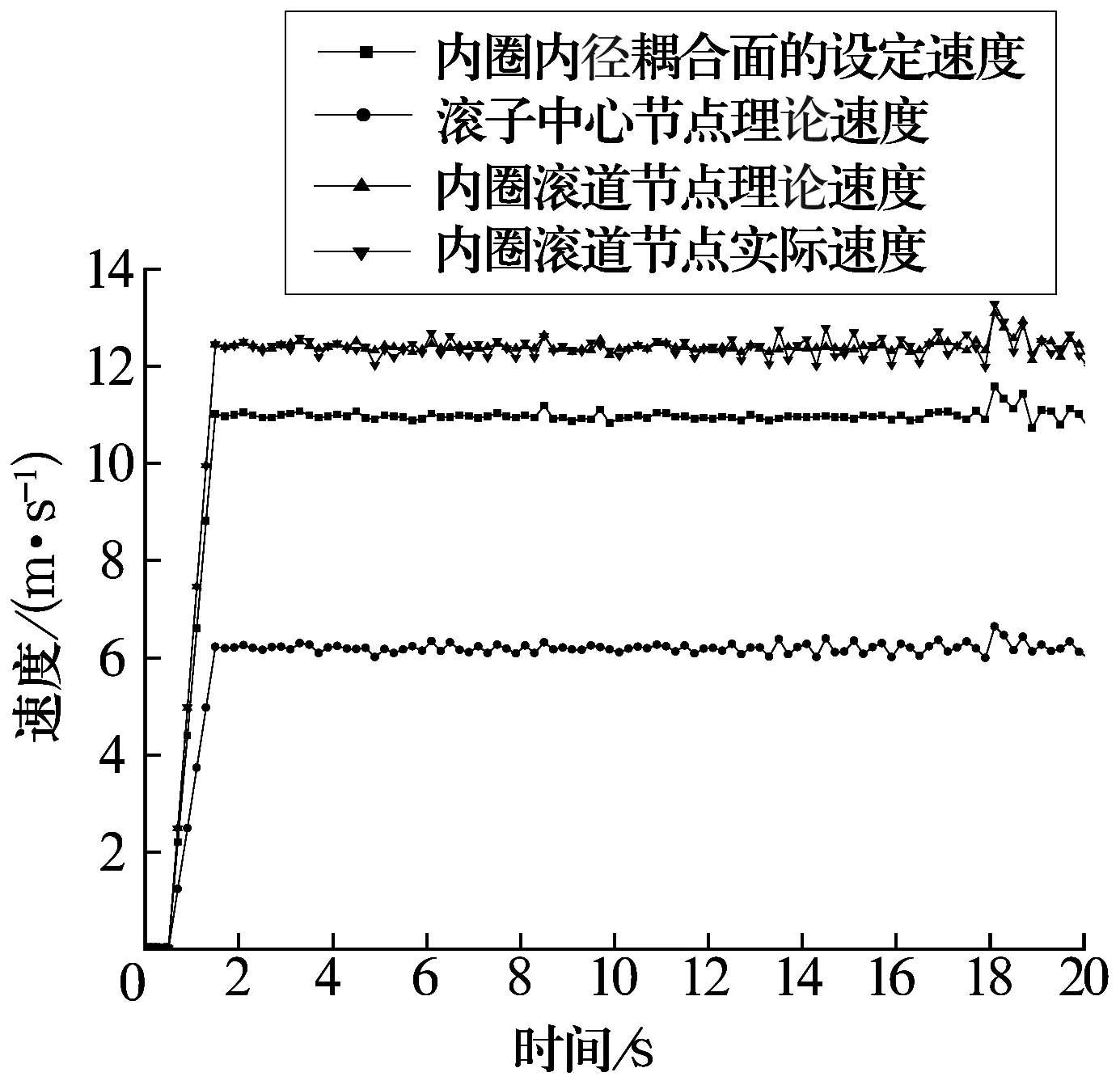
图6 内圈内径耦合面和滚道的速度

为了准确获得滚子理论速度，可假定滚子与滚道间为纯滚动。由图4可知，滚子的速度瞬心轴位于滚子和外圈的接触线，可用内圈滚道上和滚子接触处的节点速度计算滚子中心节点理论速度，也是下文计算滚子打滑率的理论速度。

3.2 滚子打滑率分析

由于轴承在运转过程中难以测量滚子的运动状态，当各运动部件未做柔性化处理时，以保持架转速和理想转速之差确定滚子打滑率是国内、外学者常用的方法，而有限元方法能将轴承各部件离散化，保持架各网格质点运动参数也会存在波动性，为了方便判断滚子打滑率，提取图5所示的两节点速度计算滚子打滑率为[4]

(8)

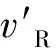
内圈转速为2 075 r/min，径向载荷为2.32 kN，过盈配合产生的压力为200 MPa时，内圈旋转滚子的理论速度和实际速度如图7所示。内圈不旋转时，滚子速度非常小，可视为处于静止状态；内圈旋转时，滚子依靠内圈间的摩擦力而旋转，滚子运动速度滞后于内圈运动速度，且在增加到一定值后不再增加。

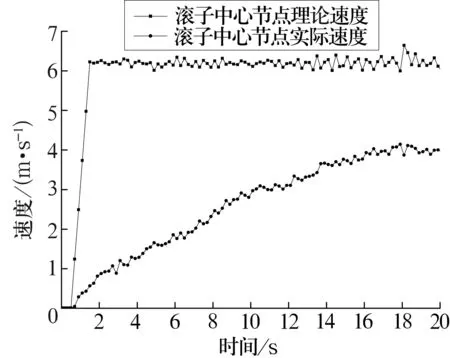
图7 内圈旋转滚子的理论速度和实际速度

内圈转速为2 075 r/min，过盈配合产生的压力为200 MPa，不同径向载荷下的滚子打滑率如图8所示。在滚子打滑率随径向载荷的增加而减小的过程中，滚子速度产生波动，且波幅随时间的增加而增大。

轴承进入稳态后，滚子打滑率的平均值随径向载荷变化的规律如图9所示。滚子打滑率随径向载荷的增加而减小，两者间呈非线性关系。

径向载荷为5.80 kN，过盈配合产生的压力为0，不同内圈转速下的滚子打滑率如图10所示。滚子打滑率随内圈转速增大而减小，滚子打滑率越小，波幅随时间的增加变化越大。

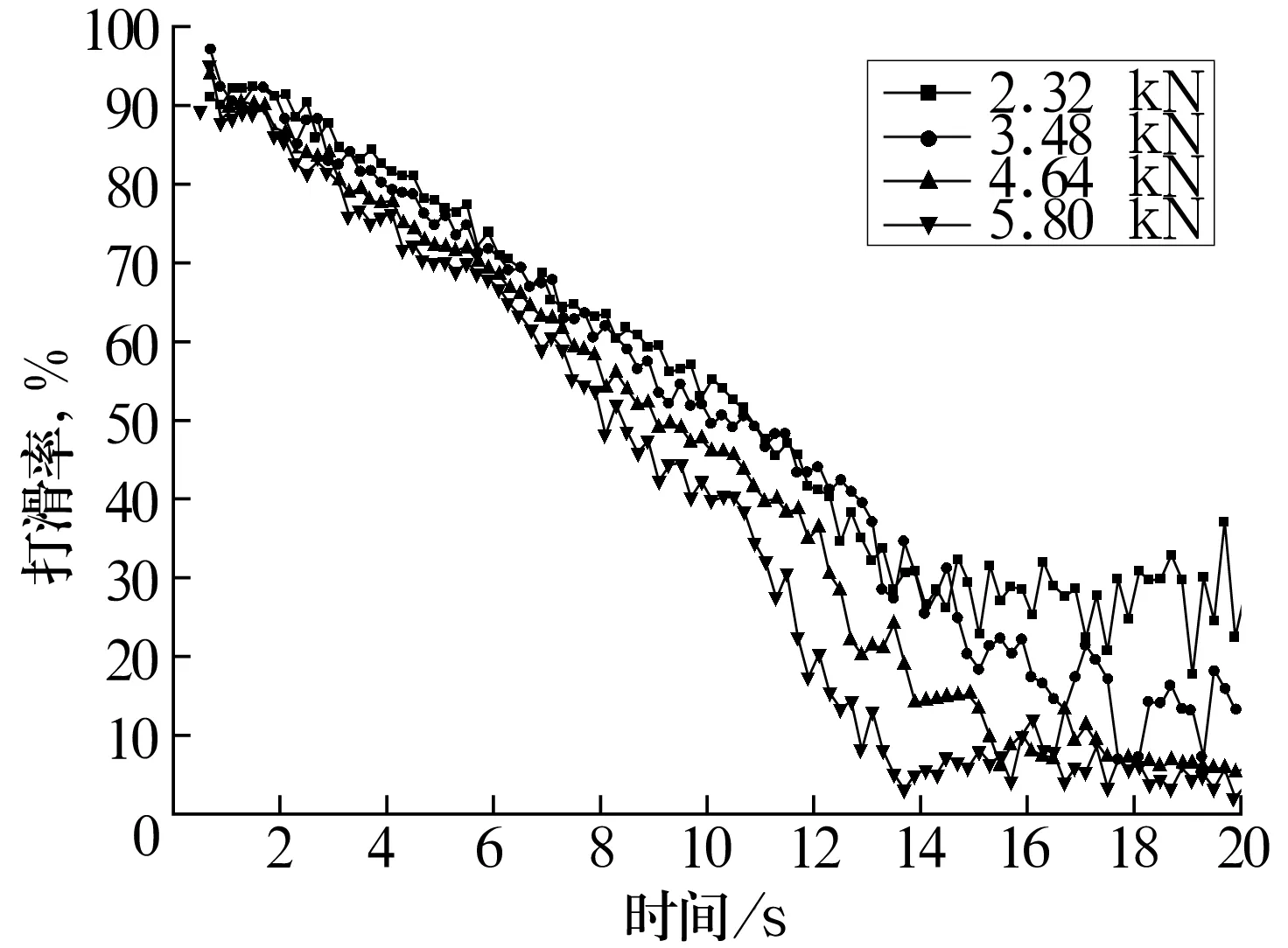
图8 不同径向载荷下的滚子打滑率

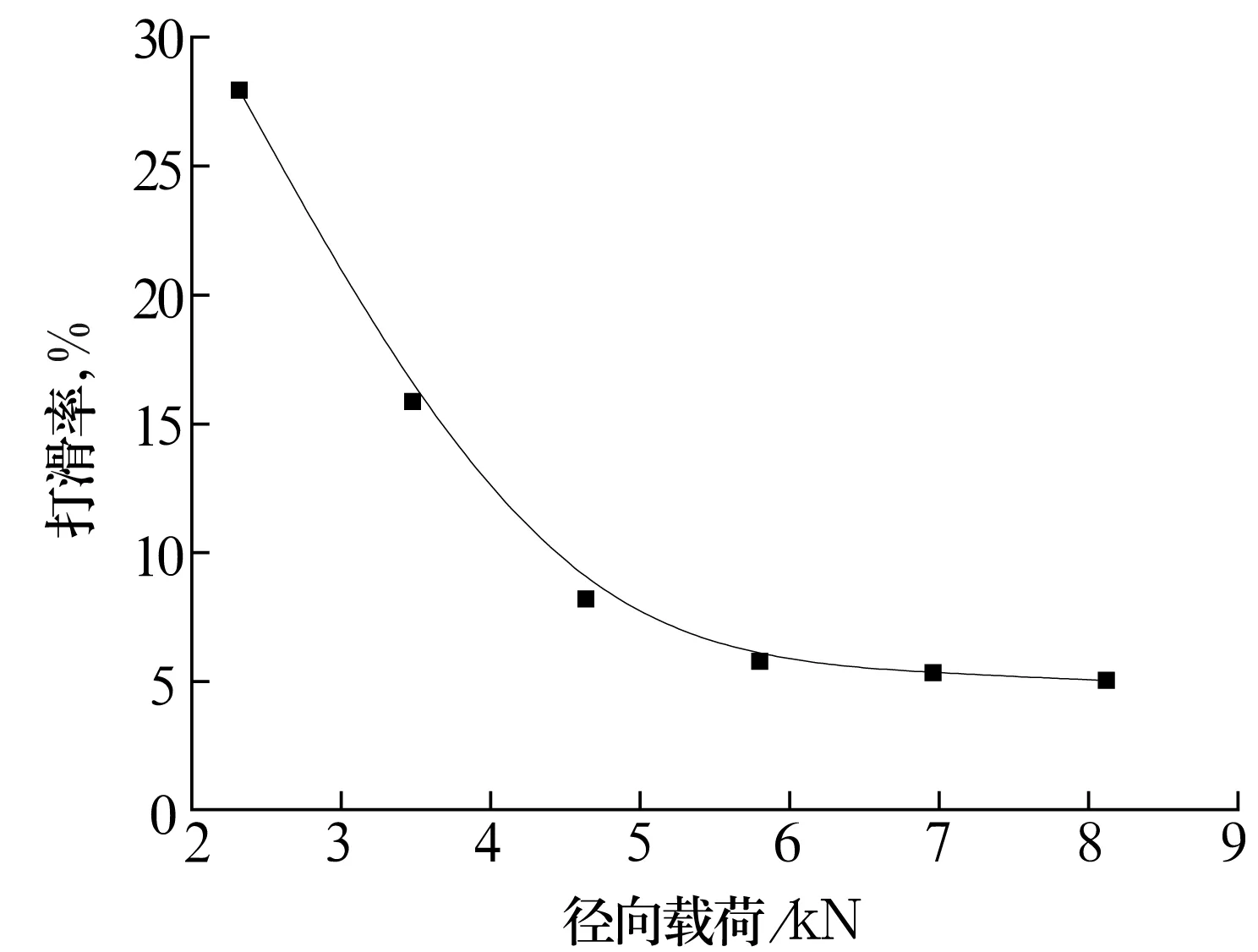
图9 滚子打滑率的平均值随径向载荷变化的规律

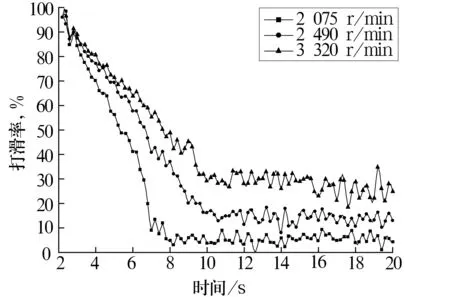
图10 不同内圈转速下的滚子打滑率

轴承进入稳态后，滚子打滑率的平均值随内圈转速变化的规律如图11所示。在相同工况下，内圈转速对滚子打滑率影响很大，两者间呈非线性关系。

图11 滚子打滑率的平均值随内圈转速变化的规律

内圈转速为3 320 r/min，径向载荷为2.32 kN，不同过盈配合产生的压力下的滚子打滑率如图12所示。滚子打滑率随内圈旋转而产生，随过盈配合产生的压力增加而下降，随时间增加而趋于稳定，同时伴有波动。

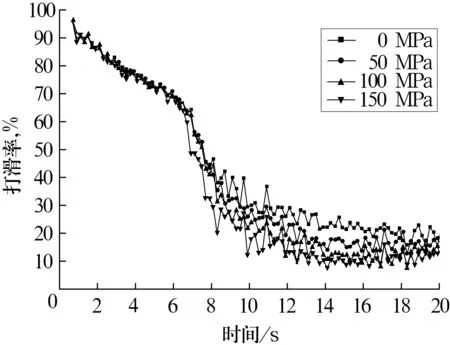
图12 不同过盈配合产生的压力下的滚子打滑率

轴承进入稳态(即15s)后，滚子打滑率的平均值随过盈配合产生的压力的变化如图13所示。滚子打滑率随过盈配合产生的压力的增加而减小。

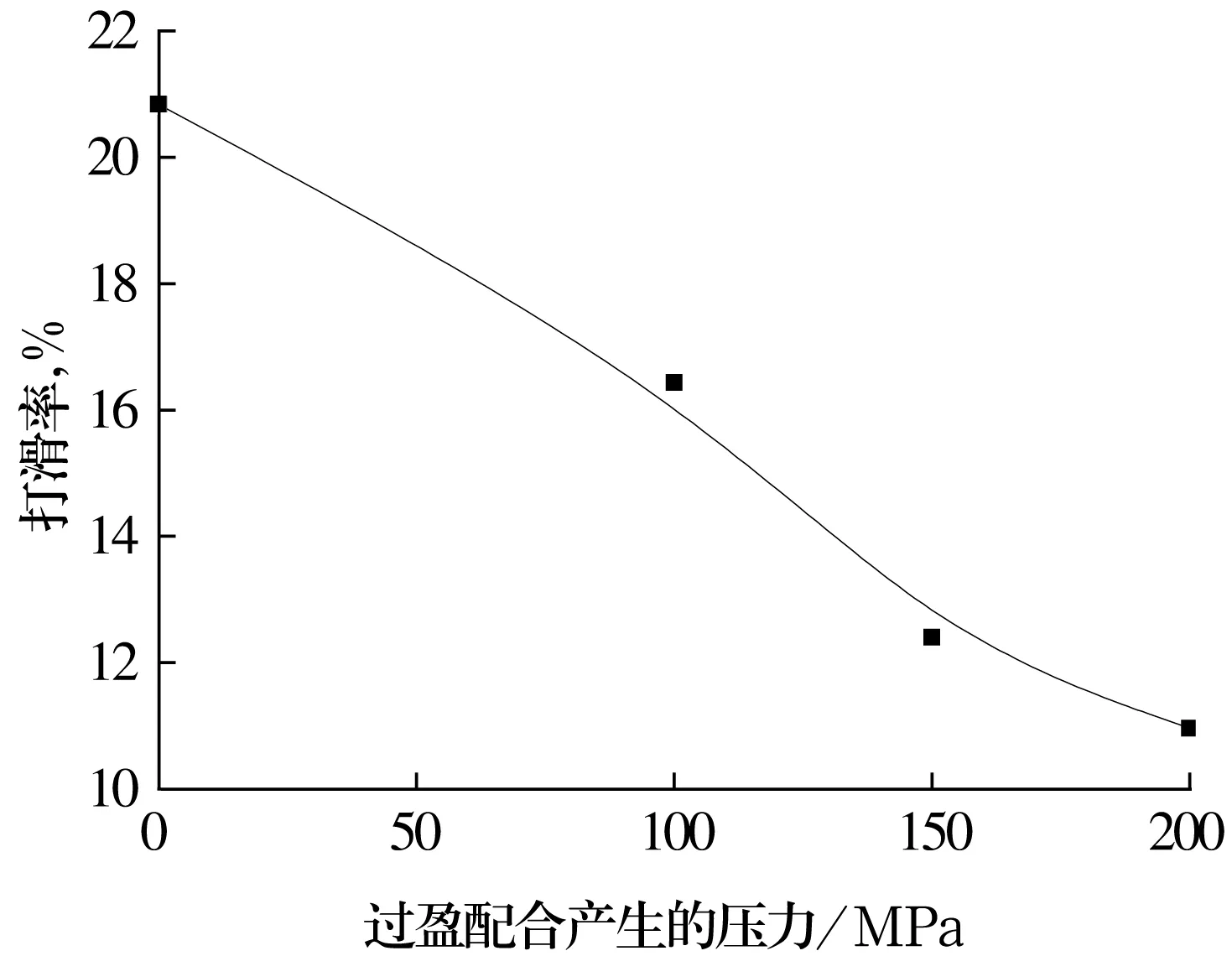
图13 滚子打滑率的平均值随过盈配合产生压力的变化

4 结论

(1)通过对滚子与滚道间进行柔性化处理，依据显式动力学理论和柔性连续体的应力波动计算，可获得轴承运动部件各节点的速度变化历程，为滚子打滑机理研究提供有效的计算方法。

(2)轴承启动过程中，随内圈转速增加，滚子和保持架速度滞后于内圈速度增加。随内圈速度趋于稳定，滚子和保持架速度滞后于内圈速度趋于稳定。计算得到的滚子打滑率也逐渐下降并趋于稳定，且稳定后的打滑率存在一定波动。

(3)内圈转速和径向载荷对滚子打滑有较大影响，高速轻载工况下滚子打滑严重，随径向载荷的增加和内圈转速的减小，可一定程度消除滚子打滑。在内圈转速和径向载荷无法改变时，增加内圈与轴的过盈配合产生的压力可有效降低滚子打滑率。