浮环轴承结构参数对其动态特性的影响

2014-07-21易圣先赵俊生殷琼

轴承 2014年3期

易圣先，赵俊生，殷琼

(中北大学机械工程与自动化学院，太原 030051)

1 前言

浮环轴承在航空航天以及精密加工机床等领域应用广泛。如图1所示，浮环轴承较常规轴承具有一定特殊性，在轴承和轴颈之间有1个浮动套，当轴颈或轴承旋转时在摩擦力作用下可使之转动，转动速度达到一定值时，将原径向滑动轴承的1个摩擦副变成了浮动套内外2个摩擦副，使得每个摩擦副的相对滑动速度都低于原轴承，具有摩擦功耗低、寿命长和稳定性好等特点[1]。

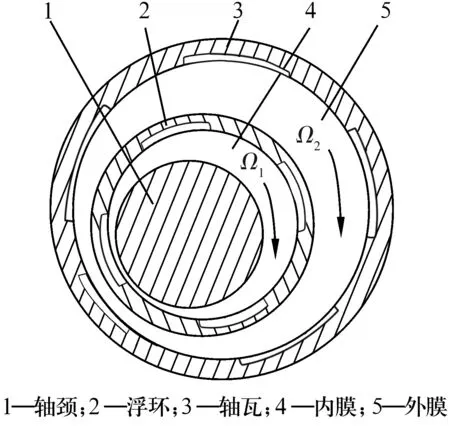
图1 浮环轴承结构示意图

国内外很多学者对不同工况下的动静压轴承进行了大量研究，尤其是在非线性领域和高速运转时的稳定性方面[2]。文献[3]研究了浮环涡动特性，得到了稳态时浮环质心运动轨迹为椭圆形的结论；文献[1]采用将浮环轴承内外2层油膜刚度系数和阻尼系数进行串并联的方法建模，对不同转速和偏心率下浮环动静压轴承的稳定性进行了研究。但是在浮环轴承结构参数对其润滑性能影响方面均未做系统的研究。

下文基于摩擦学和流体动力润滑理论，探讨了索氏数、内外膜偏心率在润滑过程中与间隙比及浮环内外半径比的变化规律,得出浮环轴承总刚度和总阻尼与其结构参数的变化关系。

2 润滑特性分析

2.1 润滑基本方程

浮环内表面与轴颈间的油膜称为内膜,浮环外表面与轴瓦间的油膜称为外膜[5]。由力的平衡表明，浮环中心不移动且以等速转动，润滑介质在内外间隙中的流动服从Reynolds方程[4]

式中：x为轴承周向线坐标；z为轴向坐标。

2.2 轴承平衡条件

如图1所示，对于浮环轴承，当浮环稳定旋转时，根据平衡条件，浮动套上内、外油膜压力产生的合力相等，但方向相反，并且内外2个摩擦副作用在浮环上的摩擦力矩亦相等[5]，即

W1=W2，

(1)

M1=M2或F1R1=F2R2，

(2)

式中：R1，R2为浮环内、外半径；Wi为承载力；Mi为油膜作用在浮环上的摩擦力矩；Fi为油膜摩擦力；下标i为“1”时对应内层油膜，为“2”时对应外层油膜(下同)。

2.3 数值分析推导

浮动轴承油膜被浮动套隔开，在分析时可视为由2套滑动轴承组成，则

内膜U1=R1ω1,U2=R1ω2，

外膜U1=R2ω2,U2=0，

式中：ω1，ω2分别为轴颈、浮环角速度。为计算方便，对计算模型无量纲化

式中：Ci为油膜间隙；pi为油膜压力；εi为偏心率；hi为油膜厚度；ηi为内外油膜黏度；l为轴承长度；θi为从最大膜厚量起的角向坐标；R为半径；η0i为无量纲参量。

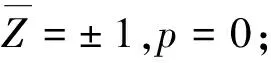
采用超松弛迭代差分方程求出油膜压力分布，然后利用积分计算出油膜承载力、偏位角和摩擦力矩。

(3)

(4)

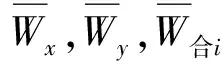
内膜摩擦力

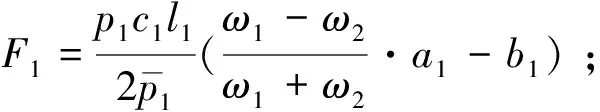
(5)

外膜摩擦力

(6)

影响油膜厚度的参数有很多，常用相似理论中的相似数归纳它们的综合关系，则

式中：S为表示轴承承载能力的索氏数[5]；Wj为轴瓦所受载荷；Wr为浮环所受载荷；ψ为内、外膜相对间隙。

由于外摩擦副相对速度小于内摩擦副，且油膜厚度小于内摩擦副，承载能力比内膜低，因此着重研究外膜索氏数。根据上述推导，用超松弛迭代进行求解，可得结构参数与外膜索氏数之间的关系曲线如图2和图3所示。

由图2可知，内间隙不变时，外膜索氏数与间隙比呈反比关系；外间隙不变时外膜索氏数随着间隙比的增加而增大。由于间隙比增大，则内间隙必然增大，而内间隙的增大也会使外膜承载能力增强。

图2 不同间隙比时外膜索氏数

图3 不同半径比时外膜索氏数

由图3可知，浮环内外半径比与外膜索氏数呈正比关系，并随之增加而增大，且内间隙不变时增加的趋势较快，此时由于半径比的增大导致外间隙增加，索氏数增大，外膜间隙与外膜索氏数也呈正比关系。

根据合力及力矩平衡条件，将(3)～(6)式代入(1)和(2)式可得

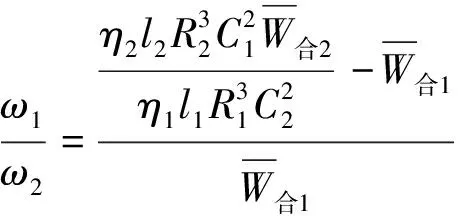
(7)

由于内外膜温度与转速有关，且热效应对浮环内外层油膜的黏度比影响非常显著，且有公式[7]

式中：fη(n)，fd(n)，fc(n)分别为黏度比、直径比、间隙比随转速变化的函数；k为比例系数；Ω2为浮环转速；Ω1为轴颈转速。

由于Reynolds方程是变系数偏微分方程，联立(3)和(4)式，根据转速比与间隙比、半径比的关系，采用迭代法进行求解，计算得出内外膜偏心率与结构参数的关系，结果见表1和表2。

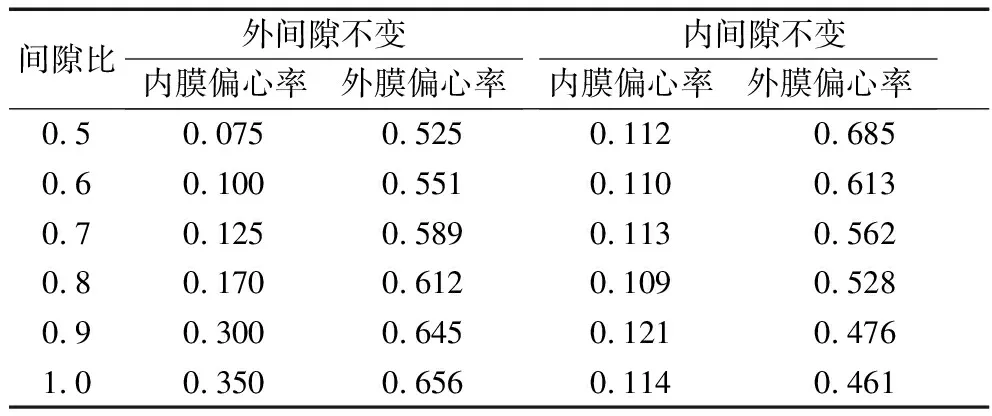
表1 不同间隙比时内外膜偏心率

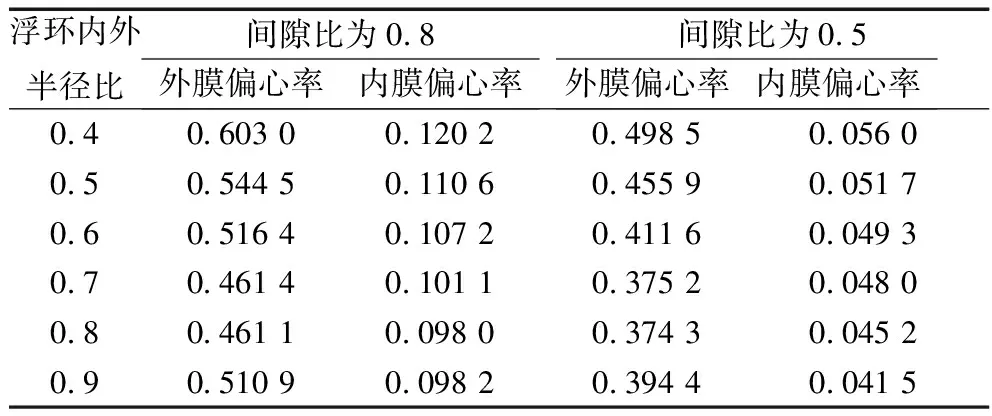
表2 不同半径比时内外膜偏心率

2.4 结构参数与偏心率的关系

由表1可以看出，不论是外膜偏心率还是内膜偏心率，当外间隙固定时，都随间隙比增大而增加；当内间隙固定时，内膜偏心率基本不变，外膜偏心率则越来越小。

由表2可知，当半径比一定时，间隙比越大偏心率越大；当间隙比固定时，偏心率与浮环内外半径比呈反比关系，但是当半径比增加到一定程度时，二者偏心率均基本稳定，或呈略微增大的趋势。

总之，外膜偏心率始终大于内膜偏心率；且内外膜偏心率与其相应间隙呈正比关系，间隙越大，偏心率也越大。

3 动态特性分析

由于浮环轴承有内外2层油膜，故与其对应有2个Reynolds方程。根据轴承润滑基本理论得出浮环轴承内外膜动态Reynolds方程为

U1=Ω1+Ω2,U2=Ω2，

Δ2=

式中：ei为偏心距；ri和αi分别为柱坐标极径和极角。

油膜的作用相当于弹簧和阻尼，将浮环轴承视为由2套滑动轴承组成，浮环轴承油膜总刚度和总阻尼都分别为内外层油膜刚度和阻尼的串联，则总刚度和总阻尼的表达式[8]为

式中：K为刚度；C为阻尼。

设P为轴颈在平衡处因微扰动所产生的油膜压力，根据小扰动线性化假设，将P写成一阶Taylor级数展开

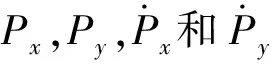
(10)

式中：x0，y0为平衡位置坐标。

将(10)式代入瞬态二维Reynolds方程，由于内外膜求解原理相同，故只取内膜作为分析对象，并引入无量纲参量

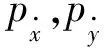
(11)

由于这些扰动压力边界条件是在完整油膜的全部边界上，故扰动压力均为零[6]。计算时采用超松弛迭代差分方程，先求出轴心静平衡位置的油膜压力，再由(11)式计算各扰动压力。将计算结果代入下式[6]即可得出无量纲刚度和阻尼

求解外膜刚度和阻尼与内膜同理。将求得的内外膜刚度和阻尼代入(9)式，同时根据上述推导的偏心率与各结构参数的变化关系，联立计算获得浮环轴承总刚度和阻尼与结构参数的关系，结果见表3和表4。

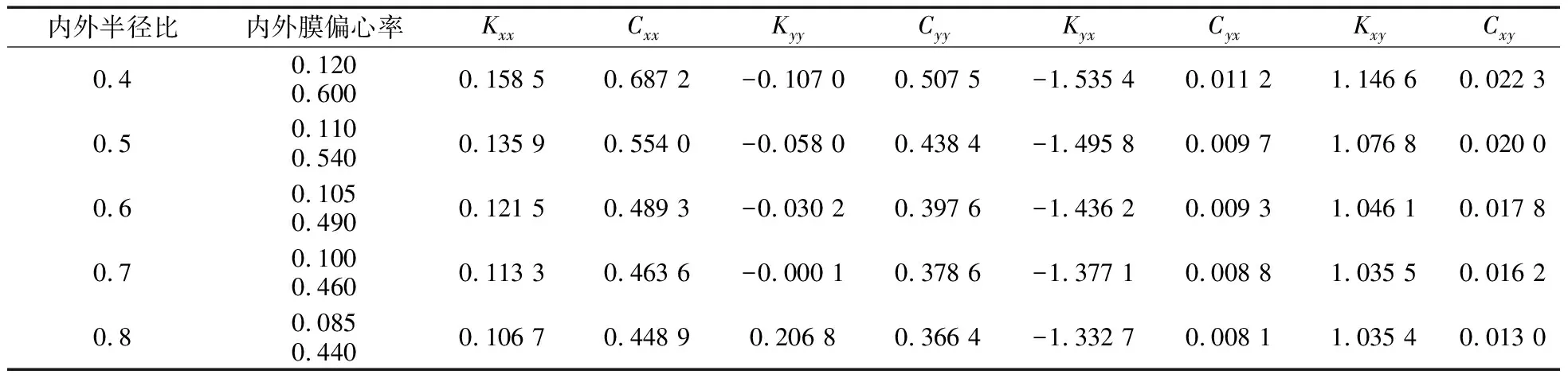
表3 不同内外半径比时浮环轴承总刚度(N/m)和总阻尼(N·s·m)

表4 不同间隙比时浮环轴承总刚度(N/m)和总阻尼(N·s·m)

由表3和表4可知，无论是间隙比增加还是内外半径比增大，浮环轴承总主阻尼均呈减小趋势；总交叉阻尼与内外半径比呈反比关系，而与间隙比则呈正比关系；随着内外半径比的增加，总主刚度和总交叉刚度的绝对值整体都呈减小趋势；间隙比增加时总主刚度的绝对值呈增加趋势，但总交叉刚度的绝对值则不逐渐减小。同时不论是间隙比的增加还是半径比的增加，因x方向扰动的总交叉刚度始终是负值，y方向扰动的总交叉刚度始终是正值，而y方向的总主刚度有正有负，这将会影响浮环轴承工作的稳定性。