轨道转换车导向轮轴承失效机理

李伟建，贾立德

(酒泉卫星发射中心，甘肃 酒泉 732750)

1 问题的提出

轴承是重要的机械基础件，在航天发射场有着广泛的应用，塔架回转平台，轨道转换车行走轮、导向轮组件，脐带塔电缆摆杆竖直杆回转机构等均使用了各类大中型轴承。近年来，随着发射场发射任务的增多，轴承的可靠性成为发射场地面设备维护与管理中的突出问题。近期，在发射场对轨道转换车(图1)进行检修的过程中，发现轨道转换车发生了导向轮下沉的故障。

图1 轨道转换车局部图

经拆解发现导向轮用NUP238型圆柱滚子轴承发生了如图2所示的损坏。下文针对导向轮轴承发生这种形式的损坏进行深入分析，以期找出失效的原因，避免今后再发生类似的故障。

图2 损坏的导向轮轴承外圈

2 冲击载荷计算分析

轨道转换车从轨道转换车改造的历史情况可以看出，多次发生因地槽变形导致的跑偏现象，而一旦出现跑偏，必将在导向轮与轮轨之间产生强烈的冲击载荷。这种冲击载荷对导向轮轴承性能的影响不容忽视，下面分正常纠偏和受地槽变形影响纠偏2种情况计算导向轮所受的冲击载荷，并进行对比分析。

2.1 正常纠偏时的冲击载荷

在正常行走过程中，轨道转换车导向轮组件需要不断对其行走轨迹进行纠偏，纠偏原理如图3所示。

图3 轨道转换车正常纠偏示意图

假设沿轨道的方向为y方向，垂直于轨道的方向为x方向，轨道转换车运行速度为v，由于轨道转换车走偏，其运行速度v与方向y的夹角为θ。工程上，为避免冲击问题分析求解的复杂性，通常采用静态等效的方法对该冲击载荷值进行估算，利用基本的动量定理得

FtΔt=mΔv，

(1)

式中：Ft为水平冲击载荷；Δt为冲击过程作用时间；m为系统的质量，此处即为轨道转换车的质量，m=200 t；Δv为冲击过程作用前后的速度变化量。不妨设轨道转换车的某次冲击载荷作用时间为0.01 s(冲击载荷的作用时间通常为毫秒级)，轨道转换车正常运行速度为3.28 m/min，冲击载荷作用后轨道转换车反向行驶。通过对轨道转换车轨距偏差、轮距偏差的测量发现，地槽轨道在y方向上每2个相邻测量点之间的轨距偏差均小于其轨距偏差最大设计值7 mm。考虑最恶劣的工作状况，即设计极限情况进行计算，设在y方向1 m距离内x方向走偏距离为7 mm，此时计算得到的冲击载荷将最大。

当tanθ=7/1 000，则θ=0.401°，Δv=2vsinθ=7.653×10-4m/s，则水平冲击载荷Ft约为15.306 kN。轨道斜面比例为1∶10，则轴向载荷为1.56 kN，而该型轴承可承受的最大轴向载荷Fmax为[1]

(2)

式中:K为与轴承尺寸系列相关的系数，K=0.2；C0r为基本额定静载荷，C0r=76.02 t；极限转速ng=1 300 r/min；n为轴承工作转速，n=1.577 r/min，可计算出Fmax=149.8 kN，远大于正常纠偏时轴向冲击载荷1.56 kN。由此可知，导向轮系统在正常纠偏过程中轴承所承受的轴向冲击载荷远小于其轴向理论承载能力，表明轴承设计选型合理，能满足正常工作要求。

2.2 地槽变形时引起的冲击载荷

地槽变形使轨道转换车卡死时车体位置示意图如图4所示，图中2为轨道转换车正常行驶时车体的位置，此时，导向轮组件与地槽轨道的两侧间隙均为δ。图中1，3为轨道转换车受地槽变形的影响，轨道转换车台车与地槽立面、导向轮与地槽钢轨共同作用，导致轨道转换车卡死时车体的2种位置。

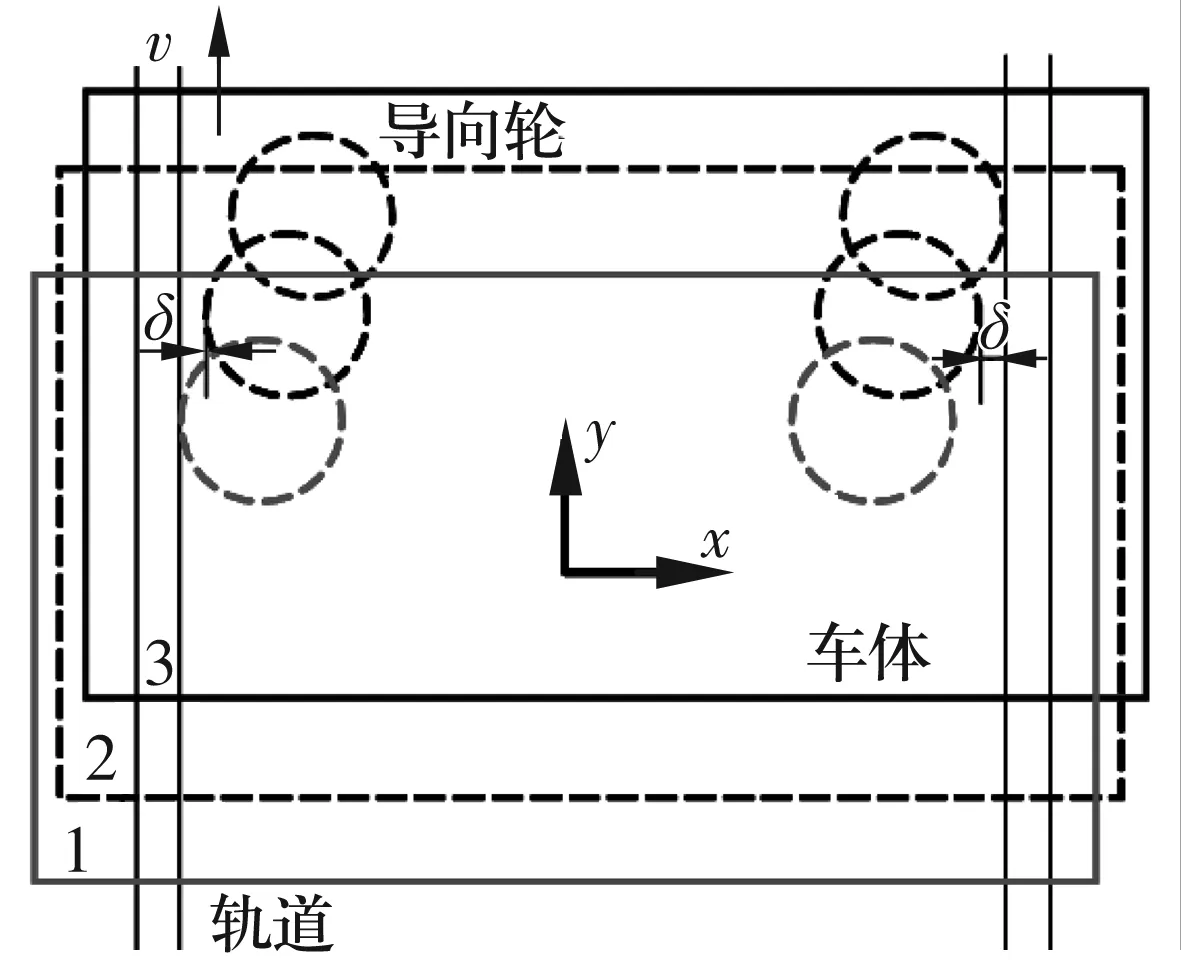
图4 轨道转换车卡死时车体位置示意图

与2.1节的分析相似，取冲击作用时间Δt=0.01 s，在此时间内发生的水平位移δ=3.5 mm(即由图中位置2偏向位置3卡死，或由位置2偏向位置1卡死)，则x方向的速度变化量Δv=δ/Δt=0.35 m/s。也即受地槽变形的影响，轨道转换车沿x方向以速度Δv撞击地槽钢轨，最终因轴承失效导致停车(卡死)。

由(1)式可以计算出此次撞击过程中的水平冲击载荷Ft=7 000 kN，轴向载荷为714.29 kN，大于轴承轴向的理论承载能力149.8 kN。

由以上分析可以看出，受地槽变形的影响，轨道转换车在运行过程中若发生卡死现象，对导向轮轴承产生的轴向冲击载荷将远大于轴承理论轴向承载能力，在该冲击载荷的反复作用下，轴承将直接发生断裂。

3 轴承失效机理分析

3.1 轴向载荷分布的计算[2]

通过对故障轴承的初步分析发现，2套轴承外圈挡边均为磨损断裂，下面重点分析轴承外圈的受力情况。轨道转换车行走过程中发生纠偏时，导向轮与轨道间存在接触，导向轮和轴承外圈的受力情况如图5所示。图中F为外载荷；F1，F2分别为轴向、径向载荷。

1—透盖；2—轴;3—导向轮;4—外圈;5—闷盖;6—挡板;7—内圈

为了简化分析，假设有2个滚子位于图5所示位置，不考虑其他滚子的受力情况。由图中的受力关系，可得轴向力平衡方程为

Qa=F1+Qb，

(3)

轴承中心弯矩平衡方程为

Qara+Qbrb=F1R，

(4)

式中：ra，rb分别为Qa，Qb作用点至轴线的距离，rG=rb；R为外载荷F作用点至轴线的距离。取ra=rb=150 mm，R=340 mm，F1=714.29 kN，即700 kN，则由(3)，(4)式可以求解出Qa=1 143 kN，Qb=443 kN，其方向如图5所示。正是由于轴承轴向受载不均及左右方向分布不同的特点，致使轴承外圈左侧下挡边及外圈右侧上挡边受滚子端面接触载荷的作用，且左侧接触载荷较大。导向轮、透盖和闷盖通过轴承悬挂在导向轮轴上，轴承外圈无有效的固定支撑，外圈挡边厚度为10.5 mm，相对于滚子尺寸和有效支撑的内圈挡边而言，是整个结构的薄弱环节。在接触载荷Qa，Qb的作用下，将产生应力集中，工作时不断磨损，当磨损到一定程度或出现外载荷过大时，轴承外圈上、下挡边就会突然断裂。

3.2 内外圈轴线夹角的计算

如图6所示，轴承外圈在F2的作用下将产生位移δr，其中心由O移到O′，在F1的作用下，内圈中心线与外圈初始中心线形成夹角θ1。

图6 内外圈轴线倾斜示意图

不考虑外圈挡边的弯曲变形，滚子变形与载荷的关系为

(5)

式中：lw为滚子长度；E为弹性模量，E=206 GPa;S为滚子截面面积。由文献[3]可知，NUP238型轴承外形尺寸为：内径190 mm，外径340 mm，宽度55 mm，滚子组内径231 mm、外径299 mm，滚子尺寸为φ34 mm×34 mm。结合(3)，(4)式中计算得到的Qa，则δa=0.207 8 mm。由图6几何关系可近似计算θ1为

(6)

式中：r为滚子中心线到轴承中心线的距离，由滚子组内、外径计算得r=132.5 mm，则θ1=0.090°。

在F2的作用下，内圈中心线与外圈初始中心线形成的夹角θ2，可根据悬臂梁挠度公式计算为[4]

(7)

式中：F2=7 000 kN；l=445 mm；I=πd4/64；d=190 mm。经计算得θ2=3.013°。

因此，轴承内、外圈轴线夹角θ=θ1+θ2=3.103°。在工作弯矩作用下，轴承内、外圈倾斜会使其寿命急剧下降，这是由于工作弯矩作用引起的轴承承载区域增大和接触载荷显著增加所致。此处尽管忽略了一些影响因素，但计算得到的θ值仍较大。可见在冲击载荷作用下轴承内、外圈轴线严重倾斜，将导致轴承非正常运转，从而加速轴承的损坏。

4 故障轴承检测分析

为深入揭示导向轮轴承失效的原因，由国家轴承质量监督检验中心对故障导向轮轴承进行了检验，结果如下：

(1) 轴承材料、硬度及热处理均合格，说明轴承本身质量并不是导致其失效的原因。

(2) 宏观观察及扫描电镜检验发现，断裂源起源于油沟槽与端面相接处，属于过载引起的脆性断裂。

(3) SKF NUP238圆柱滚子轴承通常不承受或只承受较小的轴向载荷，该轴承外圈挡边与油沟槽接触处是薄弱环节，易产生应力集中，故在受到较大的轴向冲击载荷时易发生断裂。

5 结论和建议

经过以上理论分析并结合国家轴承质量监督检验中心的检验，可以得到如下结论和建议：

(1) 正常纠偏过程中，轨道转换车所产生的轴向冲击载荷小于轴承的轴向承载能力，理论上是安全的。

(2) 地槽变形致使车体卡死过程中所产生的轴向冲击载荷远远超过轴承的轴向承载能力，该冲击载荷的反复冲击使轴承外圈挡边处产生过载和应力集中，导致轴承外圈挡边磨损断裂，轴承内、外圈分离，最终发生导向轮下沉故障。

(3) 由于圆柱滚子轴承NUP238不宜承受较大的轴向载荷，故可能存在设计选型不当的问题。

鉴于航天任务高密度常态化的发展趋势，建议后续检测检修过程中应加强发射工位大型轴承的状态监测，尤其是润滑状态检查，以提高地面设备轴承的寿命和可靠性；添置相应的检测仪器，提高对设备的检测能力，通过开展专项研究，提升中心地面设备的综合保障水平，确保发射任务的顺利实施。