滚动轴承动力学模型研究进展

2014-07-21刘保国孟华

轴承 2014年2期

关键词：保持架分析模型外圈

刘保国, 孟华

(河南工业大学，郑州 450000)

随着机械工业的发展，对滚动轴承的精度、性能、寿命和可靠性要求越来越高，其中对轴承动态性能的研究尤为重要，为此，下文对轴承动力学模型研究进展进行论述。

1 轴承动力学模型研究

1.1 发展历程

轴承力学模型经历静力学分析模型、拟静力学分析模型、动力学分析模型3个发展阶段。早期仅根据理想的运动状态和简单的运动关系建立静力学分析模型，很难准确预测和描述轴承运动状态。拟静力学分析模型相对完善，可有效预测滚动体转速、轴承疲劳寿命、轴承变形和刚度等运动参数，可基本满足工程需要，但不能分析轴承瞬态不稳定现象，也不能完整描述轴承动态性能。动力学分析模型不仅可有效分析轴承的载荷和转速随时间变化时的工作状态及滚动体和保持架的稳定性等，而且可更真实准确地描述轴承的动态和稳态运动，所以近些年动力学分析方法的研究开始得到重视。

高速轴承动态性能分析始于20世纪60年代，文献[1-2]最早对轴承拟静力学问题进行讨论和分析，在传统静力学分析的基础上提出套圈滚道控制理论，假设滚动体的运动状态是纯滚动，无自旋运动，同时在对高速转动下的轴承进行受力分析时考虑陀螺力矩和离心率的作用，但模型中未考虑弹性润滑的作用，不能正确预测轴承的内部滑动。随着弹流理论的发展，文献[3]在拟静力学模型的基础上考虑润滑和惯性力的作用，建立轴承拟动力学分析模型，可分析轴承的变形、滚动体的自转和公转速度等稳定性参数，但仍不能分析轴承瞬时不稳定性及时变参数的影响等动态性能，故在此基础上研究和探索轴承动力学模型。文献[4]最早建立4自由度球轴承动力学模型，对球轴承各组件间的相互作用力进行适当简化，随后建立6自由度轴承保持架模型，开创性地分析保持架与滚动体的动态变化，利用四阶Runge-Kutta法计算滚动体与保持架的瞬时位移、转速及轴承的内部滑动等，但模型中未考虑油膜润滑和保持架的弹性问题。文献[5-6]考虑润滑状态下轴承载荷变化及保持架上的滑移，建立3自由度轴承保持架动力学模型，但由于当时对弹流润滑理论的研究不够成熟，模型有待完善。文献[7-12]较全面地分析影响轴承动态性能的各种因素，系统地研究滚动体的运动和受力状态，建立6自由度轴承动力学模型，并分别建立轴承各零部件的运动微分方程，此模型适用于各类轴承，主要用于分析轴承在变速和变载时的瞬时动态特性。

1.2 典型模型

文献[11]将轴承-双转子系统的中介轴承简化为弹簧和阻尼，利用传递矩阵法研究双转子系统的临界转速振型和不平衡响应问题。文献[11]建立的轴承模型如图1所示。图中，e为偏心距；Fu为不平衡力；Nb为滚动体个数；ωc为保持架转速；t为时间；W为垂直方向上的恒定力。

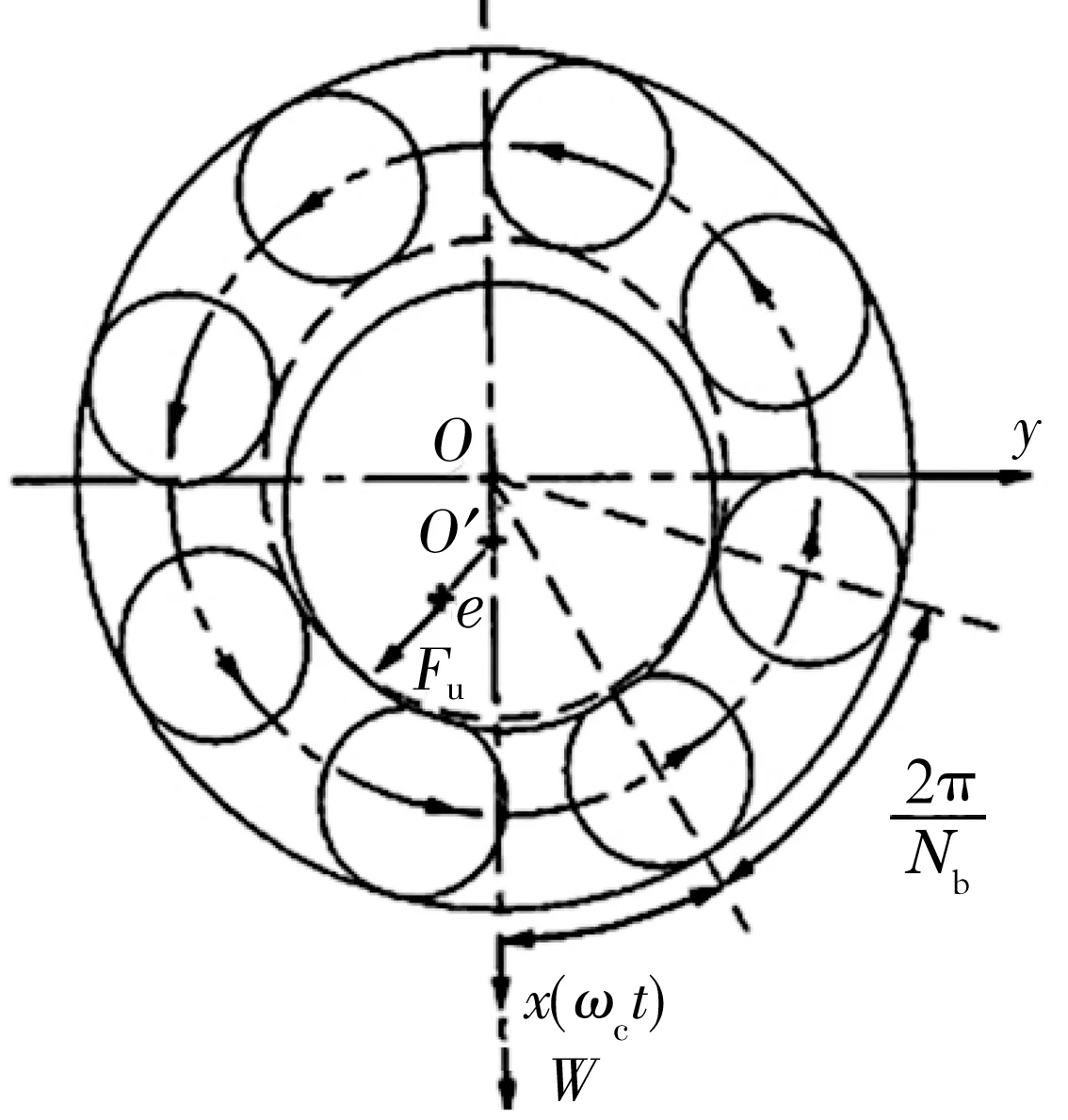
图1 轴承模型

此模型假设滚动体等距分布在轴承内部进行纯滚动运动，不考虑润滑油膜的作用。通过分析得

Fx=K∑(xcosθi+ysinθi-γo)1.5+cosθi，

(1)

Fy=K∑(xcosθi+ysinθi-γo)1.5+sinθi，

(2)

式中：Fx为x向分量的复合弹簧力；Fy为y向分量的复合弹簧力；K为Hertz接触刚度；θi为第i个滚动体处的角位置；γo为轴承径向游隙。

以此建立轴承-转子耦合系统的二阶非线性微分方程为

cosθi=W+Fucos(ωt)，

(3)

sinθi=Fusin(ωt)，

(4)

式中：m为由轴承支承的转子及轴承内圈质量；C为阻尼；ω为转子转速。

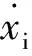
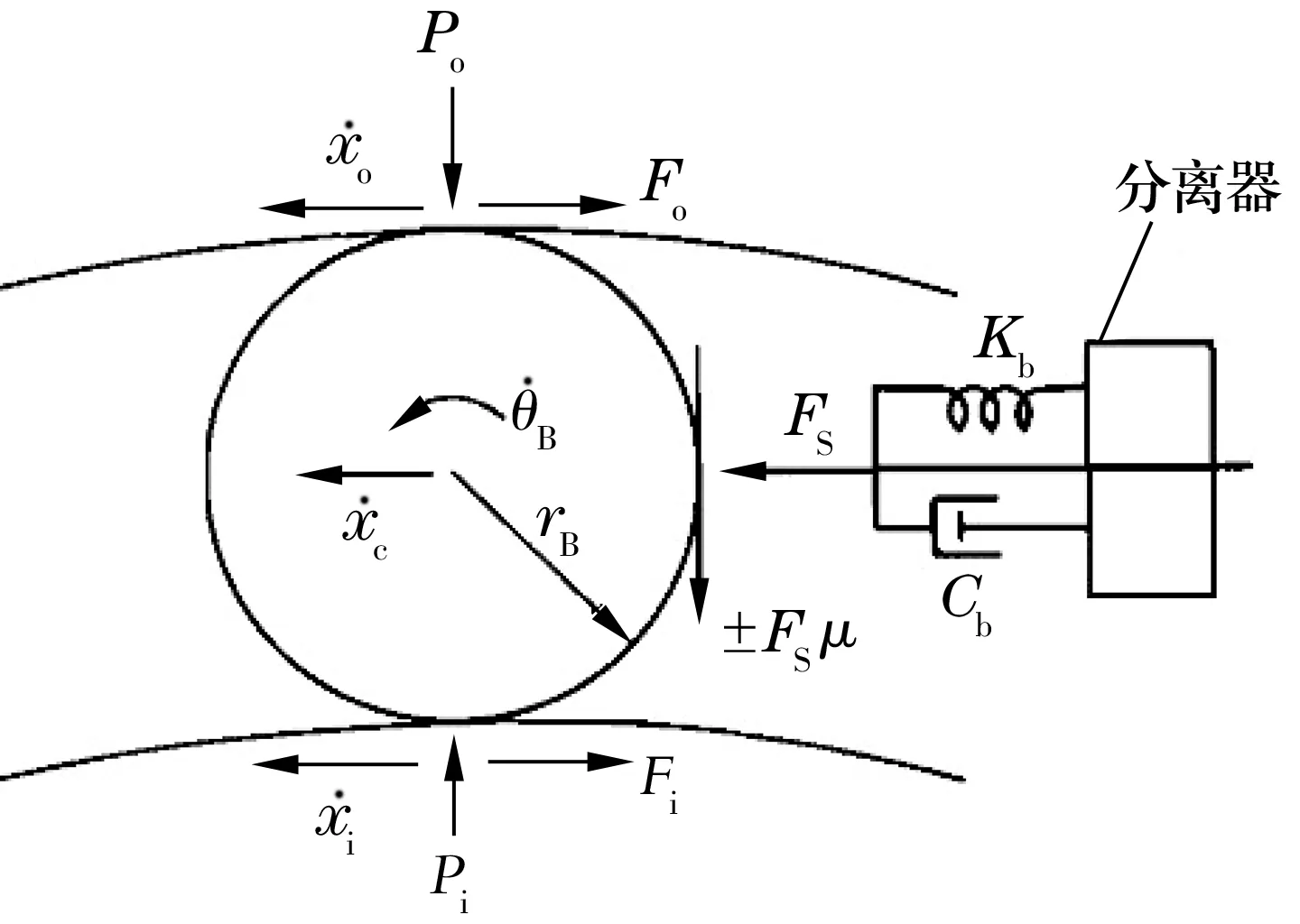
图2 轴承简化模型

此模型假设滚动体的质心在保持架轨道中心线上滑动，将其简化为一个黏性滑动阻尼，将滚动体与保持架间的相互作用简化为接触表面的法向力和滑动摩擦力作用的阻尼弹簧系统。

轴承的滑动摩擦力为

(5)

(6)

力平衡方程为

(7)

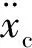
力矩平衡方程为

(8)

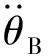
此模型可用于轴承流体润滑分析，但对轴承内部各零部件间的润滑及作用力分析较少，模型相对较简单。文献[7-16]介绍3自由度圆柱滚子轴承模型建立方法，并建立6自由度和3自由度的滚子、套圈、保持架的碰磨模型，提出建立轴承动力学模型的一般方法和步骤。文献[17]提出6自由度深沟球轴承动力学模型，模型中考虑Hertz接触变形、弹性流体动力学及轴承径向游隙等因素，还考虑轴承缺陷的影响，如内、外圈的波纹度和局部缺陷等。文献[18-19]提出一种建立含径向游隙参数的深沟球轴承支承的平面多体系统动力学模型的一般方法，模型中对深沟球轴承引入非线性动态力，考虑球与沟道之间接触刚度及接触体的几何变形和材料变形的影响，并将建立的深沟球轴承模型应用于曲柄滑块机构中验证，为轴承动力学模型的研究提供有益参考。

1.3 缺陷轴承动力学模型

轴承在制造和使用过程中难免会出现各种缺陷，有时虽不影响使用，但在运转过程中会对系统的振动响应和力学性能产生一定影响。文献[20]分析轴承打滑引起的接触表面损伤及有关轴承零部件间相互作用的动力学特性，建立轴承动力学模型。文献[21]建立轴承-转子多体系统的动力学模型，模型中考虑轴承各零部件间的接触刚度，同时研究缺陷轴承的振动频率问题，对含径向游隙及内、外圈局部缺陷的轴承进行建模，并利用模型对缺陷轴承进行分析和试验验证。文献[22]研究存在局部表面缺陷的轴承的载荷分布、油膜特性、结构弹性及轴承零部件间的滑动摩擦等问题，建立轴承的3自由度耦合模型，用于局部缺陷对轴承产生激励响应的分析。文献[23]建立内、外圈表面存在多个表面缺陷的深沟球轴承动力学模型，采用Runge-Kutta法求解耦合运动控制方程，分析含表面缺陷的保持架、套圈和球的瞬时振动频率，该模型在分析轴承缺陷振动时得到广泛应用。文献[24]改进球轴承的二维振动模型，考虑离心载荷、径向游隙及非线性Hertz接触问题，采用Newmark时域积分方法对轴承-转子系统的运动微分方程求解，研究表面缺陷和局部变形对轴承的影响。文献[25]为得到缺陷轴承的振动响应，提出一种可用于诊断轴承多种缺陷的3自由度质量-弹簧-阻尼系统动力学模型，此模型中假设轴承的油膜润滑作用是线性的，可用于诊断内、外圈及滚动体上的局部缺陷。文献[25]建立的轴承动力学简化模型如图3所示。图中，KOR，KOF，KIF，KIR，COF和CIF分别为轴承各零部件间的刚度和阻尼；MIR和MOR分别为内、外圈质量；MB为滚动体质量。

图3 轴承动力学简化模型

2 轴承-转子系统动力学模型的研究及应用

轴承不再作为单独的研究个体，而是同转子之间的相互作用共同研究，即可更真实可靠地描述轴承性能。轴承-转子系统又分为轴承-单转子系统和轴承-多转子系统，在轴承-单转子系统中轴承主要起支承作用，而在轴承-多转子系统中轴承还起连接作用，比如航空发动机的双转子系统的低压转子与高压转子间是由轴承连接的转子系统。

2.1轴承-单转子系统动力学模型

文献[26]对深沟球轴承支承的轴承-转子系统进行简化，并对比分析支承系统分别为刚性支承和柔性支承时对轴承-转子系统性能的影响，并且考虑非线性Hertz接触力、球的离心载荷、角接触力及轴向力对模型的影响。文献[27]提出一种用于研究轴承-转子系统动力学特性的轴承动力学模型，主要针对轴承的内部游隙和波纹度而建立，重点讨论波纹度、径向游隙和预紧力对保持架速度的影响。文献[28-29]在之前研究的基础上进一步考虑转子不平衡力对轴承-转子系统的影响，将轴承单元简化为质量-弹簧模型，滚动体和内、外圈间的接触被认为是非线性的弹性接触，其刚度运用Hertz接触变形理论得到，建立轴承支承的高速转子的结构振动分析模型。在建立动力学模型时，假设轴承的塑性变形小到可忽略，仅考虑Hertz理论下的弹性变形的影响，假设保持架的角速度为常量，内、外圈及转子在同一平面内运动，轴承各零部件及转子均为刚体，文献[28-29]建立的轴承质量-弹簧系统简化模型如图4所示。图中，R为外圈半径；r为内圈半径；min和mout分别为内、外圈质量；rin和rout分别为内、外圈质量中心位置；ρj为滚动体径向位置；θj为滚动体角位置；θx为滚动体与轴承内圈接触点的角位置；χj为第j个滚动体中心与轴承内圈中心的偏角；(kin)j和(kout)j分别为滚动体与内、外圈的刚度。

图4 轴承的质量-弹簧系统简化模型

波纹度是影响轴承性能的重要因素，文献[28-29]建立的轴承内、外圈波纹度动力学模型如图5所示。图中，∏0为波纹度的原始振幅；∏p为波纹度的最大振幅；j为转角范围内的滚动体个数；ωc为内圈角速度；ωy为滚动体公转角速度。

图5 轴承内、外圈波纹度动力学模型

轴承内、外圈波纹度的振幅为

(9)

式中：L为弧长；λ为波长。

2.2轴承-双转子系统动力学模型

作为连接航空发动机双转子系统中内、外转子的中介轴承，其运动状态及受力与普通支承轴承有所不同。文献[30-32]在轴承动力学和转子动力学的基础上考虑中介轴承处的耦合特性，建立双转子Hertz轴承耦合系统的非线性动力学模型，用Newmark-β积分法和Newton-Raphson迭代法对轴承-转子系统非线性动力学微分方程求解，分析转子转速、中介轴承游隙和滚子个数及支承轴承的结构参数对转子系统稳定性的影响。文献[33-40]深入研究航空发动机的双转子模型，把轴承作为航空发动机转子系统的重要零部件，建立其动力学模型，充分考虑轴承游隙、滚动体与滚道的非线性Hertz接触力及变柔性振动等因素，对轴承-双转子耦合动力学问题研究作出贡献，并且建立轴承-转子-机匣间耦合作用的动力学模型，在航空发动机轴承动力学模型方面取得一系列成果。文献[41]建立一个4自由度航空发动机主轴双转子系统动力学分析模型，该系统中双转子由2套角接触球轴承和2套深沟球轴承支承，在建立模型时考虑轴承的接触力、非线性位移和弹性变形等因素，并将其与文献[11]建立的3自由度模型及文献[42]建立的5自由度动力学模型相比，阐述轴承-转子系统的自由度对非线性动力学模型及系统动态仿真结果的影响。文献[43]在研究球轴承支承的轴承-转子系统的非线性响应时，研究带浮环的挤压油膜阻尼器的球轴承动力学模型，此模型假设内圈固定于轴上，外圈与挤压油膜阻尼器或带浮环的挤压油膜阻尼器相连，并对基于这2种油膜阻尼模型建立的不同的轴承-转子模型进行对比分析。

3 轴承动力学分析软件

利用计算机仿真技术对轴承动力学进行分析研究非常有效。仿真技术用于轴承性能分析始于20世纪50年代末，至今已取得很大进展。

目前在三维轴承零部件间相互作用力瞬态动力学分析方面取得重大进展，FAG, NSK和SKF等均为公司内部的轴承开发和设计提供验证的程序包，如BEAST三维分析软件[44]是SKF开发的轴承动力学模拟软件，可分析保持架上的力及其运动、滚子歪斜与球上的摩阻力等，并用实例验证软件的可靠性。SKF又与PELAB合作开发BEAST轴承仿真软件包，采用每个滚动体都有6个自由度的全三维模型，该软件包可进行大多数类型轴承的动力学仿真试验，使轴承动力学仿真设计成为现实[45-46]。文献[47]参考SKF美国技术中心SHABERTH的分析模型，建立油润滑球轴承动力学分析模型，利用VB和Fortran 77 语言开发高速陶瓷球轴承的动力学分析程序，可计算轴承的变形、刚度、寿命、发热和摩擦力矩等动态性能参数。文献[15]使用Fortran 90编写轴承动力学分析软件包BA的程序架构，运用此软件包可得到滚子的运动速度，滚子与内、外圈间的接触载荷与保持架质心的运动轨迹等，但是分析结果建立在很多假设的基础上，所以对滚子的受力和瞬态运动分析存在很大误差。