基于ITD和灰色关联度的轴承故障诊断方法

裴峻峰，陈园丽，代云聪，黄显茹

(常州大学 机械工程学院，江苏 常州 213016)

滚动轴承运行状态往往对整台设备的性能有很大影响，因此识别轴承运行状态具有重要的现实意义[1]。针对早前处理非平稳振动信号的各种方法的局限性，如Wigner分布对于多分量信号存在交叉干涉、小波变换的非自适应性、经验模式分解(EMD)存在较强的端点效应等一系列问题，Frei和Osorio于2007年提出一种新的非线性非平稳信号处理方法——固有时间尺度分解 (Intrinsic Time-Scale Decomposition，ITD)[2-3]。该方法能有效提取非平稳振动信号的动态特性，较好地克服上述信号处理方法的不足，取得了良好效果。下文运用 ITD法对轴承故障振动信号进行自适应分解，进而提取轴承振动信号故障特征，并针对轴承早期故障模式难以识别的问题，引入灰色关联度理论，建立轴承故障诊断模式识别模型，为轴承在线诊断提供一种新的思路和方法。

1 ITD法

作为一种最新提出的自适应信号分解方法， ITD法可将复杂的原始非平稳振动信号分解为一系列固有旋转分量(Proper Rotation Component，PRC)及一个单调的趋势信号[4]。假设Xt为待分解的原始信号，这里定义一个算子L用来抽取基线信号，如(1)式所示，从Xt中去除该基线信号后的余量作为原始信号的一个PRC。

Xt=LXt+(1-L)Xt=Lt+Ht，

(1)

式中：Lt为基线信号；Ht为PRC。确定Xt的所有极值点Xk(k=1,2,…,n)及其对应的时刻τk，通过设置分解时的线性增益α计算各基线控制点Lk，设Lt和Ht分别在[0，τk]区间上有定义，Xt在[0，τk+2]区间上同样有定义，则可在连续极值点[τk，τk+2]区间上定义Xt的基线信号抽取算子L，即

(2)

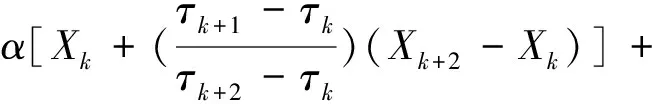
(1-α)Xk+1。

(3)

依次重复上述分解步骤即可将原始非平稳振动信号自适应地分解为不同频率范围的PRC[5-7]。

2 灰色关联度

灰色关联度分析主要基于关联度来量化灰色系统中不同因素间的相互影响与作用，通过系统内因素间的关联度来衡量因素间的相似程度[8]。假设X0={x0(j)},j=1,2,…，n为待识别模式序列，Xi={xi(j)},i=1,2,…，m;j=1,2,…，n为参考模式序列，则X0与Xi间的关联系数可表示为

γ(x0(j),xi(j))=

(4)

式中：ρ为分辨系数，常取0.5。

X0与Xi间的关联度为

(5)

对于轴承故障诊断而言，若将轴承运行状态视作一个灰色系统，则可利用γi判断轴承故障模式；若待识别模式序列与某一典型故障的参考模式序列间的关联度最大，则可认为轴承属于该类故障。

3 轴承故障诊断方法

当轴承存在局部缺陷时，振动信号中会产生由缺陷引发的脉冲冲击，在相应的故障特征频率处将出现峰值，各种故障相应的特征频率为

(6)

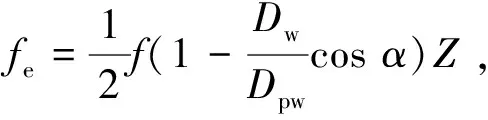
(7)

(8)

式中：fi，fe和fg分别为内圈、外圈和滚动体故障特征频率；f为轴承旋转频率；Dw为滚动体直径；Dpw为滚动体组节圆直径；α为轴承接触角；Z为滚动体数目。

由于故障信号中常包含噪声干扰，微弱的故障冲击成分往往被噪声淹没，因此减轻噪声干扰、精确提取故障冲击特征成为轴承故障诊断的关键。基于ITD和灰色关联度建立轴承故障诊断模式识别模型，其诊断流程如图1所示。具体步骤为：

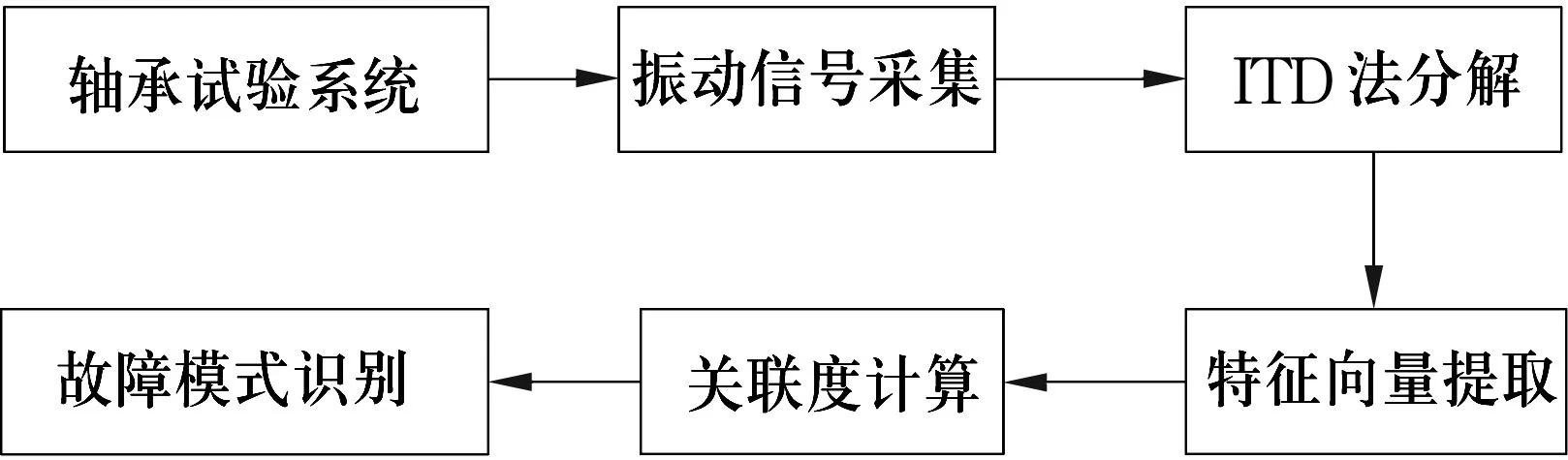
图1 基于ITD法与灰色关联度的轴承故障诊断流程

(1)基于ITD法将采集到的轴承振动信号分解为一系列PRC(PRC1,PRC2,…，PRCn)。

(2)对分解后含有明显周期性冲击成分的前K个PRC进行频谱分析，则可用Ai=[Ai1(fi),Ai1(fg),Ai2(fi),Ai2(fg)]，即第i个PRC的特征向量作为部分待识别样本向量，其中Ai1(fi)，Ai1(fg)，Ai2(fi)和Ai2(fg)分别为第i个PRC的频谱图中的轴承内圈、滚动体故障特征频率的1倍及2倍频处幅值，则待识别样本向量为

A=[A1,A2,…，An]。

(9)

(3)依照(9)式，假设存在K类典型故障状态，分别提取各类故障状态下若干组振动信号特征参数的平均值构成一个特征向量，由K个特征向量构成一个典型故障的参考特征矩阵，通过计算待识别特征向量与标准参考模式特征向量的关联度来确定轴承处于何种运行状态，进而实现轴承的实时在线监测和早期故障识别。

4 实例分析

试验采用NU206圆柱滚子轴承，通过电火花加工方法在滚子和内圈上设置的模拟故障如图2所示，轴承测试系统如图3所示。试验时径向加载14.4 kN，电动机转速为3 400 r/min，采样频率为7.5 kHz，采样长度为15 000点。依据轴承故障特征频率计算(6)～(8)式可得内圈故障特征频率为440 Hz，滚子故障特征频率为139 Hz。

图2 滚子和内圈故障

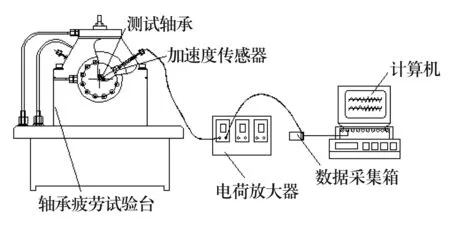
图3 轴承测试系统

为了解决ITD法分解信号边界效应的问题，对此方法进行改进，采用镜像对称延拓方法对端点效应进行处理，使分解后的轴承故障信号的边界更平滑。轴承振动信号分解图如图4所示。采用ITD法对轴承振动信号进行分解，通过对各层分量进行频谱分析发现，前3个PRC具有明显的故障冲击特征，基本包含100 Hz以上大多数成分，且轴承故障信息主要集中在高频区域，因此可判断前3个PRC包含轴承故障信号的主要信息，是信号处理的关键。

内圈故障状态下轴承振动信号经ITD法分解后的PRC1分量及其频谱图如图5所示。由图5可知，内圈故障特征频率2倍频(880 Hz)附近存在明显的谱线，说明轴承存在内圈故障。滚子故障状态下PRC2和PRC3分量及其频谱图分别如图6和图7所示。由图6和图7可知，滚子故障特征频率(139 Hz)及2倍频(278 Hz)附近有较明显的峰值，可据此判断轴承存在滚子故障。

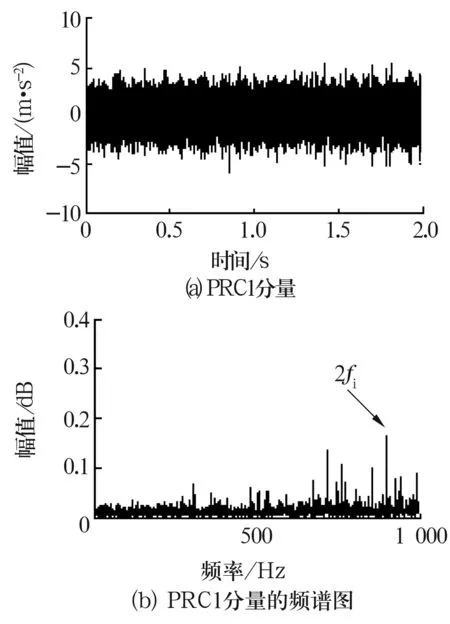
图5 内圈故障状态下PRC1分量及其频谱图

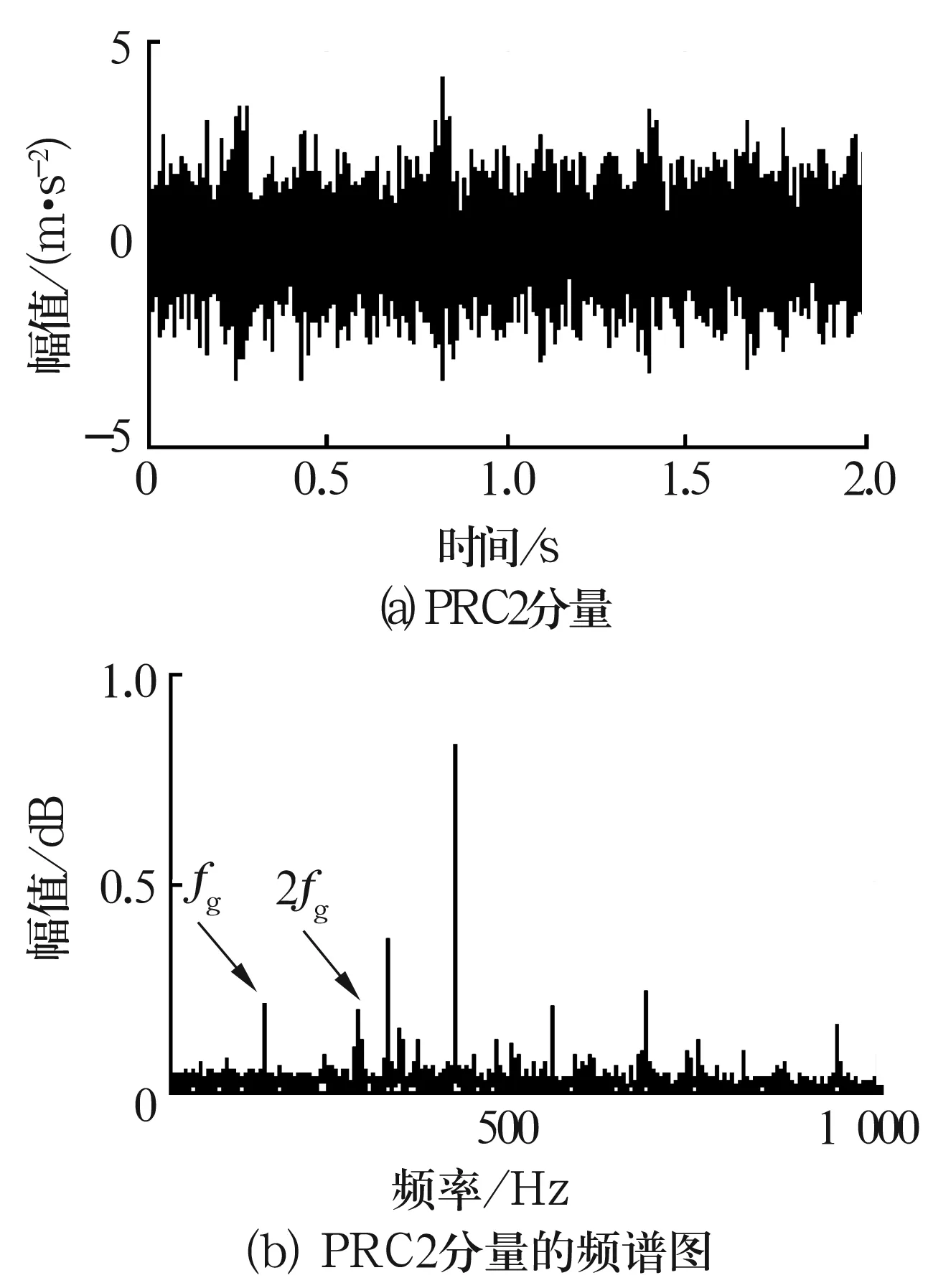
图6 滚子故障状态下PRC2分量及其频谱图

图7 滚子故障状态下PRC3分量及其频谱图

综上所述，ITD法对非平稳轴承故障振动信号有很好的分解效果，对分解后的振动信号各个主要旋转分量进行频谱分析能有效获取轴承故障特征，进而实现对轴承运行状态的可靠判断。

由于前3个PRC包含原始信号的主要信息，因此选用经ITD法分解后的前3个PRC进行频谱分析，提取故障特征频率处的幅值构成轴承故障诊断的特征向量。从各个故障类型的信号库中分别选取4组故障信号，取前3个旋转分量特征参数的平均值组成该类故障的标准参考特征向量，建立的标准参考特征向量见表1。每个故障类型分别随机选取3组故障信号，依照(9)式提取故障特征向量作为该故障类型的待识别样本来计算关联度，以识别故障，灰色关联度计算结果见表2。由表2可知，采用ITD与灰色关联度相结合的方法可准确识别轴承运行状态。

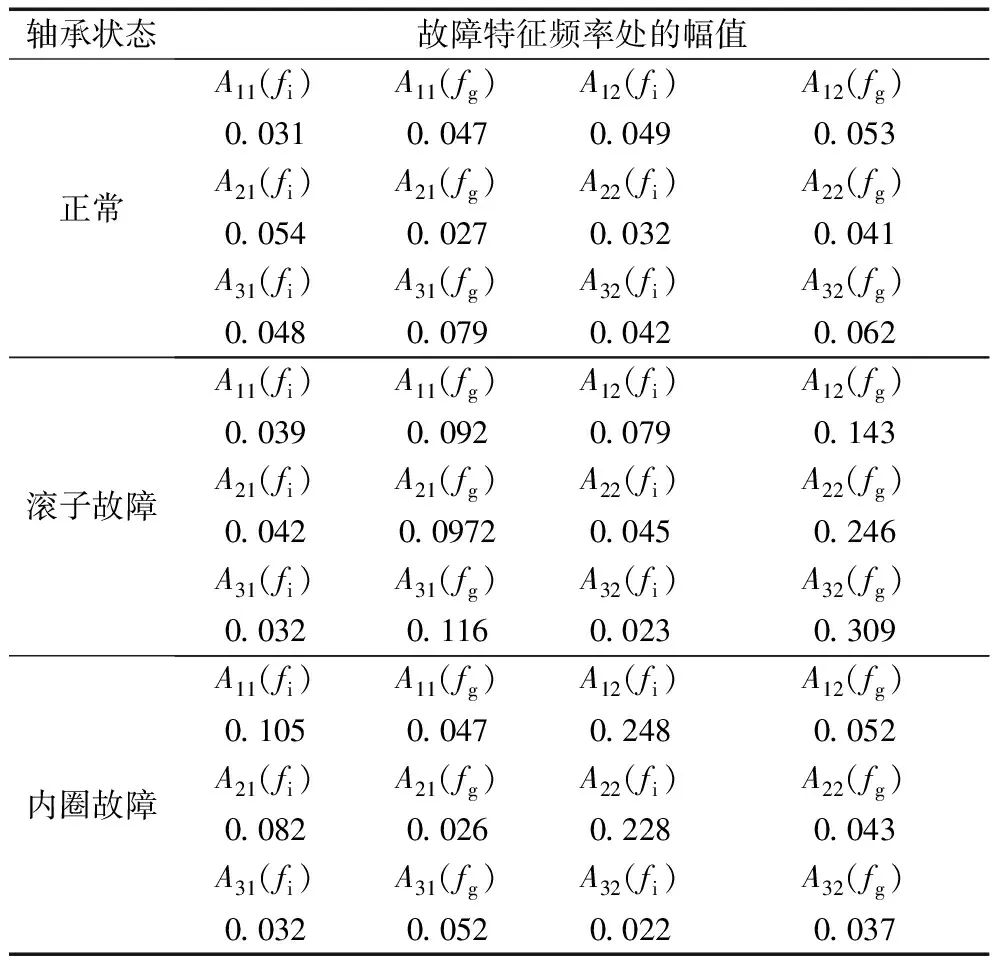
表1 标准参考特征向量

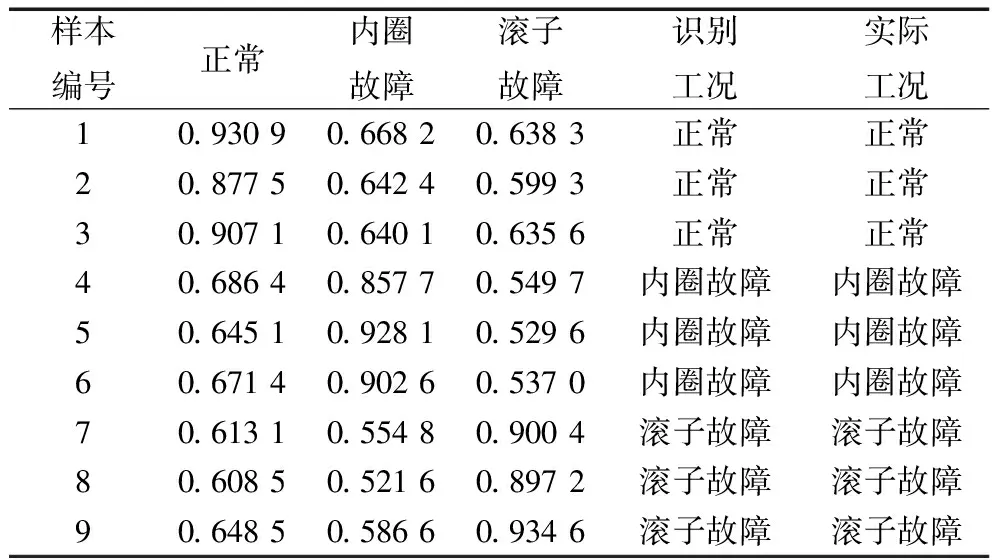
表2 灰色关联度计算结果

5 结束语

早期故障状态下能反映轴承故障信息的冲击成分往往被淹没在环境噪声及机器其他零部件引起的干扰振动信号中，使得轴承故障特征信息常常难以提取。为了有效解决这一问题，运用ITD法将轴承故障振动信号进行分解，再进一步求出各个PRC的瞬时频率进行分析，实现故障信息的有效分离和提取，并且针对轴承早期故障模式难以识别的问题，引入灰色关联度理论，建立轴承故障诊断模式识别模型。实例表明，将ITD与灰色关联度相结合可准确、有效地识别轴承的工作状态和故障类型。