圆柱滚子轴承零件几何误差对载荷分布的影响

2014-07-22王宝坤毛范海孙守林王德伦

轴承 2014年2期

王宝坤，毛范海，孙守林，王德伦

(大连理工大学机械工程学院，辽宁大连 116024)

轴承载荷分布是描述其力学特性的重要方法。尽管轴承零件具有较高的制造精度，但依然存在误差，使载荷分布产生差异，导致轴承承受冲击载荷，降低轴承寿命。

国外学者已经做了大量有关轴承的研究工作，文献[1]建立了不考虑误差情况下的轴承载荷分布模型；文献 [2]用有限元方法研究了圆柱滚子轴承套圈的应力与变形分布；文献[3]研究了滚动体误差对保持架回转中心轨迹及轴承振动的影响；文献[4]研究了轴承零件形状误差与轴心轨迹的关系。国内学者也对轴承做了深入研究。文献 [5]研究了轴承载荷与变形的关系，建立轴承载荷分布计算模型。文献 [6]研究了Hertz接触理论，通过试验得到圆柱滚子与滚道接触的修正公式。文献[7-8]研究了基于套圈轮廓的轴承旋转精度预测。

引入函数描述零件几何误差，建立考虑几何误差的轴承力学模型。研究单一误差及多种误差对载荷分布的影响，探讨不同类型误差组合对轴承载荷分布的影响规律。

1 力学模型的假设与等效

1.1 模型假设

为简化计算,建立轴承力学模型时假设:

(1)滚子仅存在直径尺寸误差；

(2)套圈滚道存在尺寸误差与几何形状误差；

(3)采用刚性套圈，即滚子与滚道的接触作用不会引起套圈整体变形；

(4)将轴承三维模型简化为二维模型，不考虑零件轴向效应及材料属性(如晶粒不均匀等)的影响。

1.2 刚度等效

基于模型假设，将每个滚子等效为2根弹簧，2根弹簧通过滚子中心节点连接，弹簧刚度分别为滚子与内、外圈滚道的接触刚度。等效弹簧为非线性弹簧，弹簧刚度与接触载荷有关。根据Hertz接触理论，滚子与内、外圈滚道的接触关系为[6]

(1)

式中：Qi，Qe为内、外圈滚道接触载荷；δi，δe为内、外圈滚道的接触变形；K1，K2为滚子与内、外圈接触刚度系数。K1，K2计算式为[6]

(2)

(3)

式中：Ei，Er，Ee为内圈、滚子、外圈的弹性模量；μi，μr，μe为内圈、滚子、外圈的泊松比；Di，Dw，De为内圈滚道直径、滚子直径、外圈滚道直径；l为滚子的有效接触长度。

刚度是指产生单位变形量所需的外载荷，对于滚子与滚道之间的接触刚度，可定义为产生单位弹性趋近量所需的接触载荷。由于接触作用是非线性的，根据(1)式接触载荷与变形量的关系，接触载荷对弹性趋近量求导，则得到滚子与内、外圈滚道间的接触刚度为

(4)

(5)

式中:Ki，Ke分别为滚子与内、外圈接触等效弹簧刚度。无载情况下弹簧长度为滚子的实际半径。接触刚度公式体现了接触载荷与变形量之间的关系，接触刚度与接触载荷有关，呈非线性变化关系。

2 等效模型的建立

2.1 零件几何误差

轴承零件几何误差具有不确定性，与制造精度有关。将滚子直径尺寸误差用离散的误差值表示，各滚子具有独立的直径尺寸误差。滚道形状误差用函数表示，函数表示轮廓上各点相对标准圆的偏差值。滚道几何形状误差有以下特点：

(1)滚道几何形状误差具有径向性，反映不同角度的半径变化；

(2)滚道几何形状误差相对于滚道半径很小，滚道基本保持为圆形；

(3)滚道实际轮廓为具有一定周期的闭合曲线，各点径向偏差不同。

滚道实际轮廓可用Fourier级数表示为

(6)

αk=arctan(ak/bk)，

式中：θ为滚道位置角；R(θ)为θ处的半径值；D为滚道标准圆直径；ak，bk为滚道实际轮廓Fourier级数展开的第k阶谐波分量的余弦项系数、正弦项系数；ck为滚道几何形状误差幅值；k为滚道几何形状误差阶次；αk为滚道误差函数初始相位；Ri,Re为内、外圈滚道实际轮廓半径。由(6)式可知滚道实际轮廓是由标准圆与若干个按不同周期变化的正弦波叠加形成。

2.2 坐标系的建立

模型需建立2个坐标系，坐标系1是以外圈滚道几何中心为原点的固定坐标系；坐标系2是以内圈滚道几何中心为原点的运动坐标系，如图1所示。

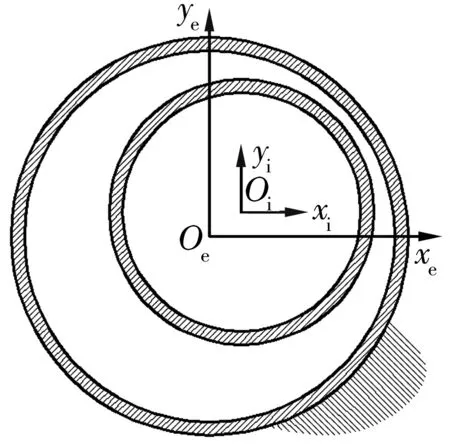
图1 模型坐标系

Oe-xeye为固定坐标系，Oi-xiyi为运动坐标系，轴承在无载荷作用时，坐标原点Oe与Oi重合。固定坐标系保持静止，运动坐标系相对于固定坐标系可移动。运动坐标系可绕其坐标原点转动来计算内圈在不同相位时的轴承载荷分布情况。

模型有2种状态，第1种是初始状态，即轴承未受外载荷作用，2坐标系原点重合；第2种是受载状态，即轴承受载荷作用，内圈与受载滚子发生偏移，轴承达到力平衡。

2.3 初始状态计算

初始状态时，内、外圈滚道几何中心重合，滚子与外圈滚道接触；轴承有正游隙；引入滚道形状误差函数表示滚道轮廓。滚子理想直径为Dr，其直径尺寸误差为Δδ(t)。固定坐标系中，将位于xe轴上的滚子定义为1号滚动体，其位置角为0°，滚子按逆时针方向分布，滚子位置角为θ(t)，滚子与外圈滚道接触处的滚道半径Re[θ(t)]是滚道误差函数，如(6)式所示。根据参数计算相关坐标。

滚子实际直径值为

Dw(t)=Dr+Δδ(t)。

(7)

滚子中心与固定坐标系原点的距离为

Rw(t)=Re[θ(t)]-0.5Dw(t)。

(8)

固定坐标系中，滚子中心节点坐标为

(9)

2.4 受载状态计算

轴承受载时，内圈与受载滚子偏移，承载区等效弹簧发生变形，总的弹簧力与外载荷平衡。以内圈与受载滚子为研究对象，计算内圈与受载滚子的偏移量。固定坐标系中，内圈沿x，y方向偏移量为u，v。首先在滚子未偏移时，判断滚子与内圈是否接触。运动坐标系中，滚子中心的坐标分别为

(10)

滚子位置角为

θ1(t)=arctan[Y1(t)/X1(t)]，

(11)

滚子中心至Oi距离为

L1(t)=X1(t)/cosθ1(t)，

(12)

滚子中心与Oi的连线与内圈滚道交点处的半径Ri[θ1(t)]是滚道误差函数，如(6)式所示。

内圈与滚子的接触情况可分为3种，分别为不接触、临界接触和有效接触。临界接触指内圈与滚子刚好接触但二者之间没有力的作用；有效接触指内圈与滚子接触且二者之间产生力的作用。

运动坐标系中，滚子与内圈滚道临界接触时，滚子中心与Oi间的距离为

L2(t)=Ri[θ1(t)]+0.5Dw(t) 。

(13)

滚子与内滚道有效接触的判定条件为

L3(t)=L2(t)-L1(t) ，

(14)

若L3(t)大于零，表示滚子与内圈滚道接触，滚子的偏移量为ε(t)≠0；若L3(t)小于零，表示滚子与内圈滚道不接触，滚子的偏移量为ε(t)=0。滚子沿内圈滚道半径方向偏移，如图2所示。

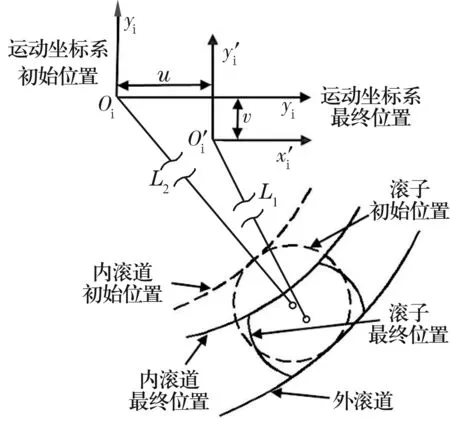
图2 滚子接触变形

滚子中心(弹簧中心)偏移量通过弹簧与内、外圈间的接触力计算确定

(15)

式中：δ为滚子总变形量，即2根弹簧总变形量L3；ε为滚子中心的偏移量。

滚子偏移后，运动坐标系中，滚子中心至Oi距离为

L4(t)=L1(t)+ε(t) 。

(16)

弹簧Ki的变形量为

δi(t)=L2(t)-L4(t)=

(17)

从(17)式可看出，弹簧变形是关于零件误差Δδ，Ri和Re的函数，可见零件几何误差影响滚子与滚道间的接触变形。

轴承内圈的平衡方程为

(18)

3 等效模型的求解与分析

3.1 求解方法

(18)式为内圈平衡方程组，其求解可得内圈的偏移量u和v，进而可计算得到轴承内部各滚子承受的载荷。

内圈平衡方程为

(19)

方程未知量为内圈沿x,y方向偏移量

δ=(u,v)T。

(20)

平衡方程分别对未知量求偏导，得到平衡方程组的雅克比矩阵J

(21)

利用Newton-Raphson法进行迭代

δ(k+1)=δ(k)-J(x(k))-1f(x(k))，

(22)

当计算精度满足计算要求后，即为平衡方程的数值解。通过内圈偏移量计算各个滚子与内圈的接触变形及接触载荷。

3.2 不考虑零件误差时轴承载荷分布计算

不考虑轴承零件几何误差(情况1)，计算轴承内部载荷分布情况。采用文献[2]中的算例，轴承结构参数、材料属性及载荷见表1。

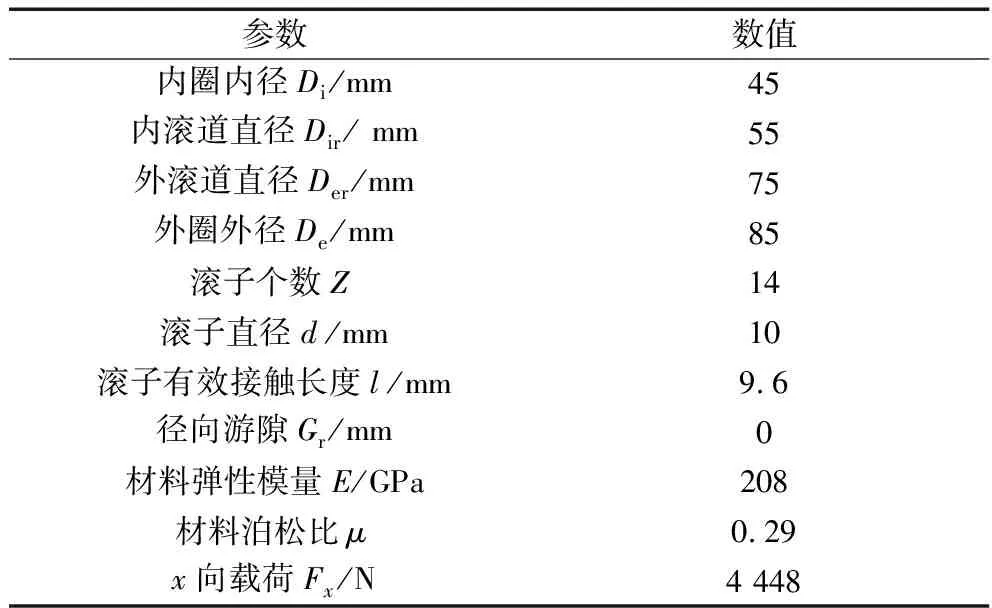
表1 轴承结构参数及材料属性

根据所建立的力学等效模型，采用3.1节的求解方法，计算轴承载荷分布情况，提取各位置角处的滚子接触载荷，并与文献[2]中的计算结果对比(表2)。

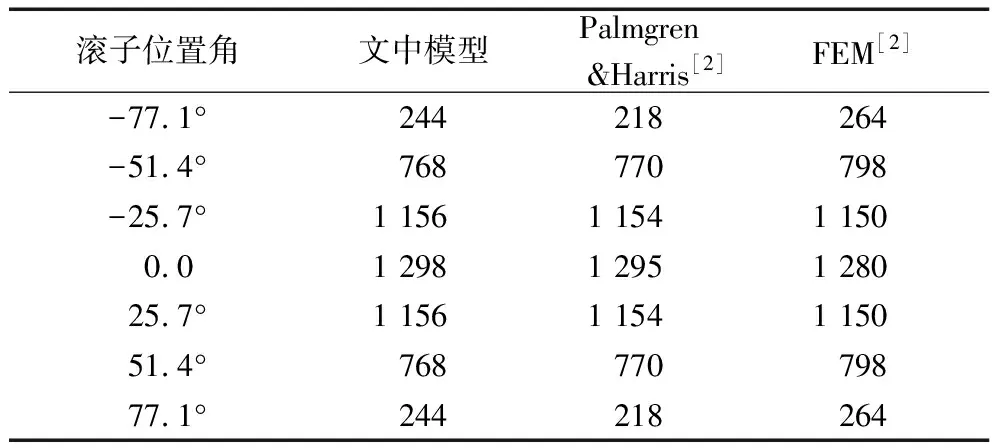
表2 不考虑零件误差的载荷分布计算结果 N

从表2可以看出，文中力学模型的计算结果与Harris模型计算结果吻合度高；与有限元计算结果基本吻合。有限元模型考虑了结构刚度的影响，受载滚子接触载荷差异为7.58%，3.76%，0.52%和1.41%。有限元计算需建立三维模型、划分网格、施加边界条件，而所建立的模型避免了有限元的大计算量，能够准确地计算各个滚子的接触载荷，将零件几何误差引入到力学模型中，分析误差对载荷分布的影响。

3.3 考虑零件误差时轴承载荷分布计算

分析零件几何误差对载荷分布的影响规律具有重要意义。以表1轴承为例，将零件几何误差引入模型中。分别考虑滚子直径尺寸误差(情况2)、内滚道形状误差(情况3)、外滚道形状误差(情况4)以及综合误差(情况5)。内、外滚道的初始相位均为0°。另外，为从理论上说明极端情况下误差对载荷分布的影响，误差值取大于实际轴承的误差值。

滚子直径尺寸误差见表3，表中数据表示14个滚子的直径尺寸误差值，滚子从0°按逆时针方向均布。考虑单一滚子与多个滚子直径误差是按照一定规律排列的，前4组为单一滚子直径误差，表示误差滚子的实际尺寸逐渐增加；后4组为多个滚子直径误差，表示误差滚子实际尺寸从0°向两侧逐渐增加或逐渐减小，能够反映滚子不同排列顺序对载荷分布的影响。计算结果如图3所示，载荷分布是关于0°对称的。

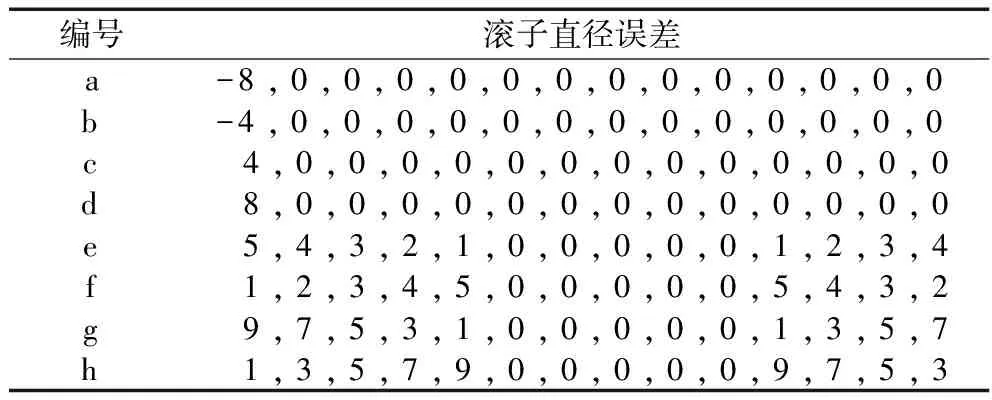
表3 滚子直径几何尺寸误差 μm

图3 考虑滚子直径尺寸误差的载荷分布

从单一滚子存在误差的计算结果可看出，当滚子直径误差为正时，且该滚子位于0°处，则其载荷将变大，并随着误差的增大滚子载荷增加，其他滚子载荷减小；当滚子直径误差为负时，且该滚子位于0°处，其载荷减小，并随着误差的增大载荷降低，其他滚子载荷增加。当单一误差滚子位于0°处时，滚子直径误差对误差滚子载荷影响较大，但承载滚子数目不变。当误差滚子未处于承载区域时，其载荷分布与不考虑零件误差时的载荷分布情况一致。

从多个滚子存在误差的计算结果可看出，情况2-h的分布顺序，即误差由0°向两侧逐渐增大，0°处滚子载荷减小，承载滚子数目增加；情况2-e的分布，即误差由0°向两侧逐渐减小，0°处滚子载荷增大。可见，滚子排列顺序影响0°处滚子的载荷，并会改变承载滚子数目。

内滚道形状误差见表4。前4组反映内滚道形状一定，形状误差幅值发生改变；后4组反映内圈形状误差幅值一定，形状改变，即阶次改变。计算结果如图4所示。

表4 内滚道几何形状误差

图4 考虑内滚道几何形状误差的载荷分布

从计算结果可看出，改变形状误差幅值时，0°处滚子载荷增加120 N左右，不同误差值所引起滚子载荷的变化不明显。改变形状阶次时，0°处滚子载荷增加200 N左右，引起滚子载荷的变化较明显。

外滚道形状误差见表5。前4组外滚道形状一定，形状误差幅值改变；后4组内圈形状误差幅值一定，形状改变，即阶次改变。计算结果如图5所示。

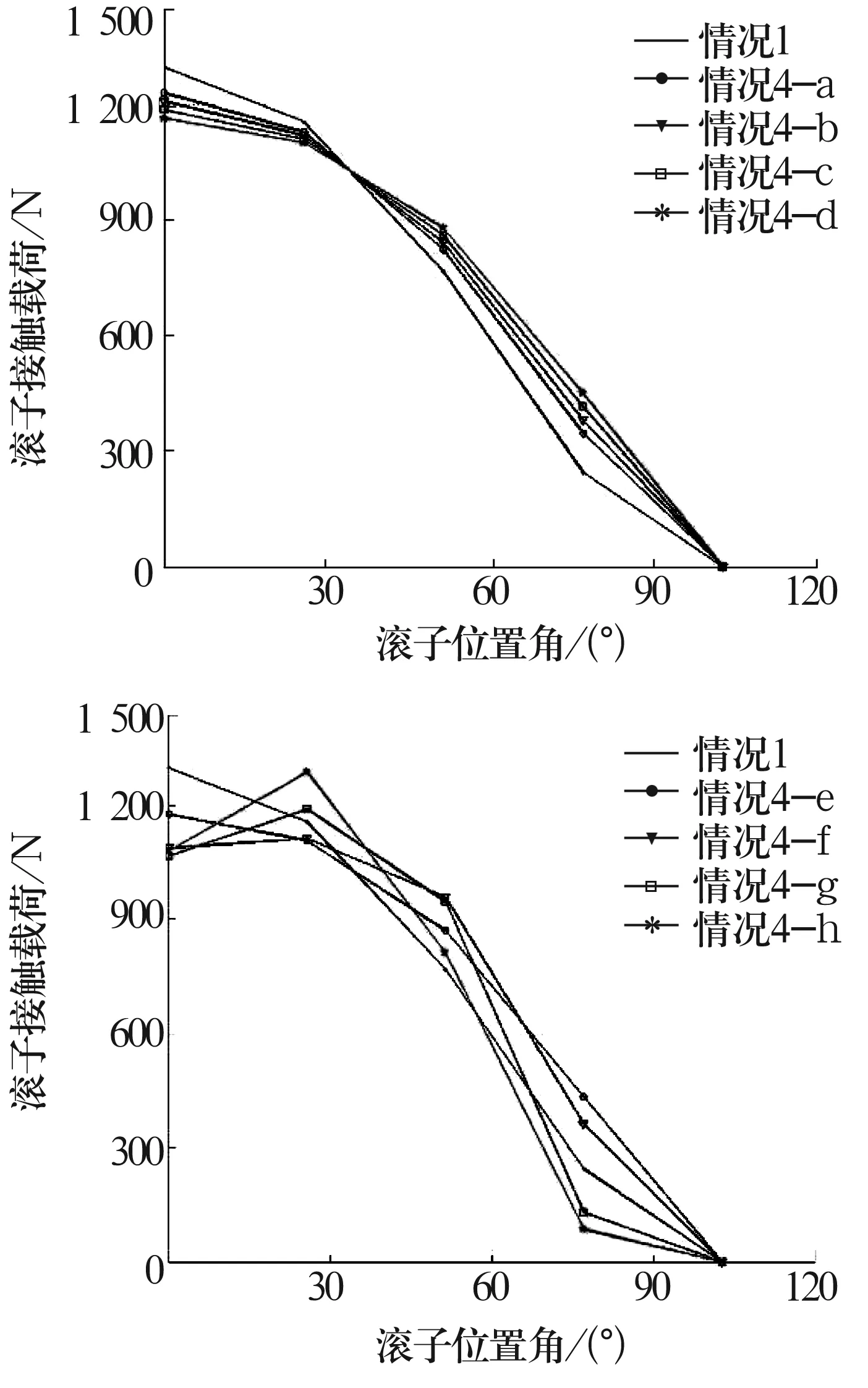
图5 考虑外滚道几何形状误差的载荷分布

表5 外滚道几何形状误差

从结果可看出，改变形状误差幅值时，0°处滚子载荷减小80 N左右，不同误差值所引起滚子载荷的变化不明显。改变形状阶次时，载荷分布变化明显，随着形状阶次的增加，0°处滚子载荷逐渐减小，有改变承载滚子数目的趋势。

为更加真实地分析几何误差与载荷分布的关系，研究多个零件几何误差对载荷分布的影响。零件误差见表6。计算结果如图6所示。

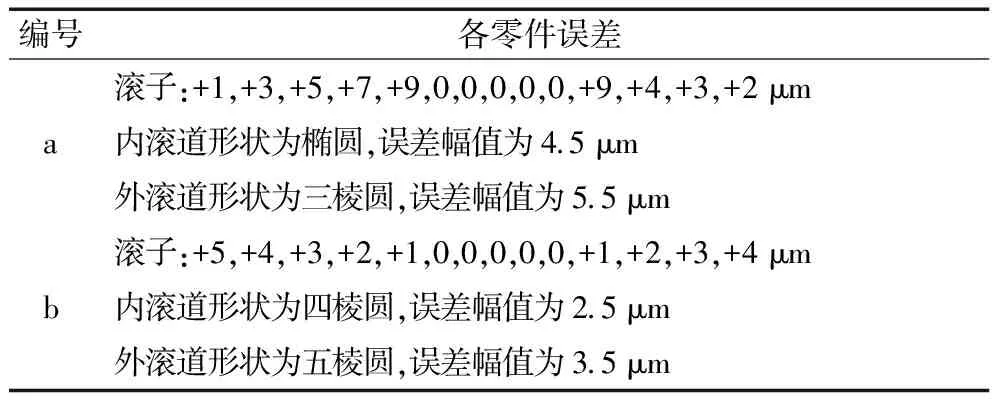
表6 多个零件几何误差

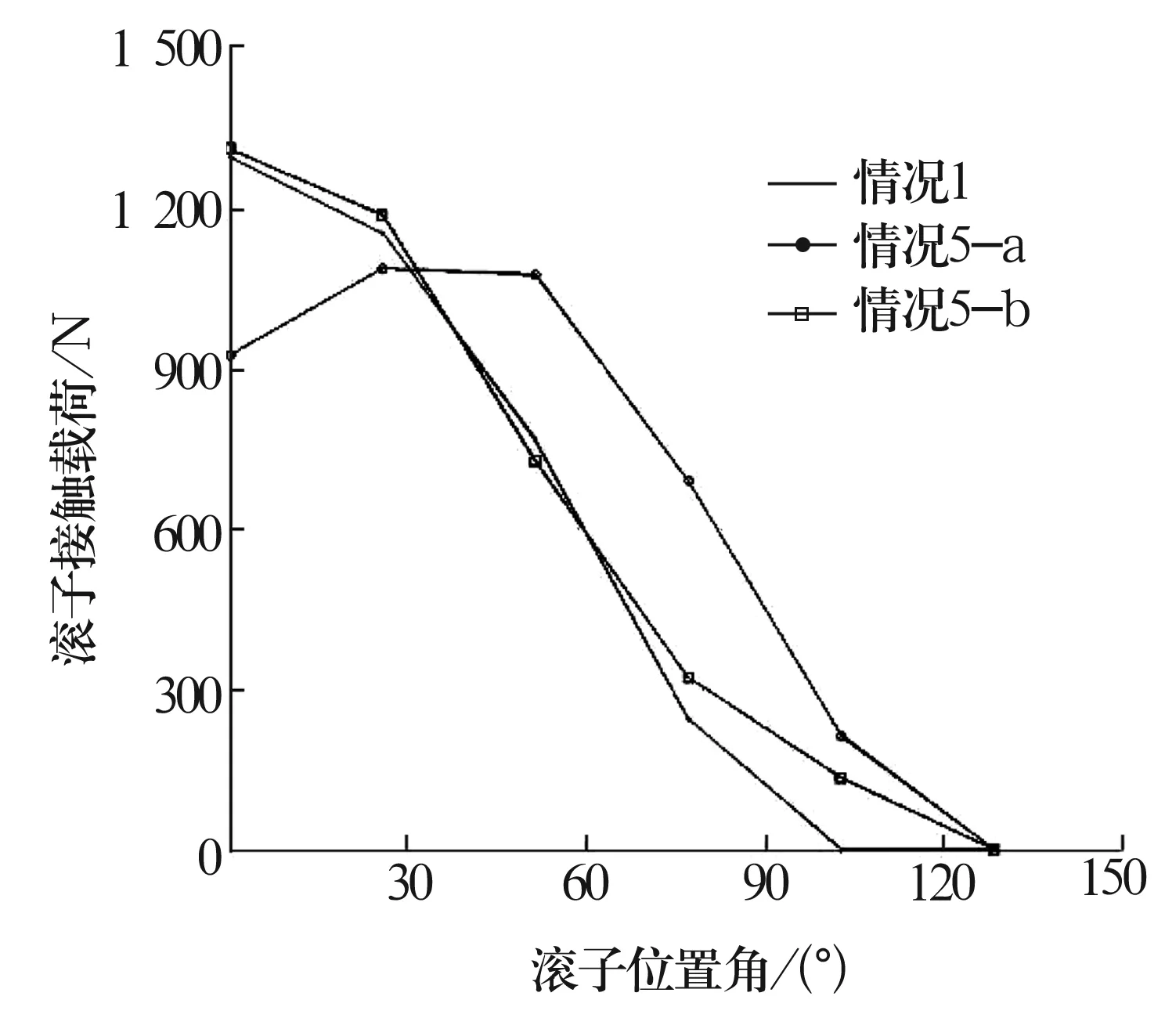
图6 考虑多个零件几何误差的载荷分布

从计算结果可看出，不同误差组合对载荷分布的影响各异。情况5-a误差组合能够优化载荷分布，减小0°处滚子载荷，增加承载滚子数目，避免内部载荷冲击。情况5-b误差组合对载荷分布影响较小，0°处滚子载荷几乎没有变化，但承载滚子数目增加。

分析单一误差对轴承载荷分布的影响，计算0°处滚子载荷变化规律，如图7所示。不考虑误差时，0°处滚子载荷为1 298.4 N。滚子载荷对单一滚子误差敏感，变化幅度大，多个滚子误差的影响与误差排列有关；内滚道形状误差使滚子载荷增大；外滚道形状误差使滚子载荷下降，但幅度不大。与形状误差幅值的影响相比，形状误差阶次对峰值载荷的影响更大。零件误差对载荷分布的影响，与误差类型、大小及误差组合有关。